2.3 Определение размеров сопл

при дозвуковых и сверхзвуковых скоростях

Процесс изменения параметров пара при расширении без учета потерь энергии происходит по адиабатному закону pv^k=const и изображается линией AD на h,s-диаграмме (рис. 2.4).

Рис. 2.4 h, s-диаграмма процессов из­менения параметров пара при его расширении без учета потерь энергии и с учетом их

В дейст­вительном процессе необходимо учитывать потери энергии. В этом случае процесс расширения пара приближенно подчиня­ется уравнению политропы

. (2.30)

Показатель политропы n для каждого конкретного случая течения должен иметь вполне определенное значение, зависящее от сил трения, но он всегда больше показателя изоэнтропы k, т. е. n > k . Этот формальный прием значительно облегчает мате­матическое исследование различных случаев течения пара с учетом вязкости. Однако следует иметь в виду, что применение eго имеет ограничения, так как действительный процесс при течении с трением не является строго политропным.

Таким образом, из-за действия сил трения при течении пара часть механической энергии превращается в теплоту трения. В результате энтропия газа при его теплоизолированном течении возрастает и в этом случае процесс в h,s-диаграмме изображает­ся кривой АС. Как видно из рис. 2.4 при одинаковом перепаде давлений (р₀—p₁) энталь­пия в конечном состоянии при течении с трением (точ­ка С) будет больше энталь­пии в конечном состоянии при течении без трения (точка D).

Из уравнения сохранения энергии (2.15) следует, что располагаемый теплоперепад

(2.31)

больше действительного теплоперепада

(2.32)

на значение потерь энергии

_. (2.33)

Отношение скорости пара c₁ в действительном процессе АС к теоретической скорости пара c_1t в идеальном (т. е. протекающем без трения) процессе AD, происходящих при одинаковом перепаде давлений, называют коэффициентом скорости

. (2.34)

Из уравнения сохранения энергии

где — так называемый располагаемый теплоперепад по параметрам торможения.

Таким образом, для определения скорости те­чения пара при наличии трения нужно вычислить скорость иде­ального течения и умножить полученное значение на коэффициент скорости φ. Коэффициенты скорости в разных соплах раз­личны, и их значения определяют опытным путем. Для сопл сов­ременных турбин они изменяются от 0,95 до 0,98.

При течении пара часть его кинетической энергии вследствие действия сил трения необратимо превращается в теплоту, вы­деляющуюся в поток. Эта теплота компенсирует уменьшение внутренней энергии пара, т. е. повышает его температуру и ра­боту расширения. Часть теплоты трения, затрачиваемая на ра­боту расширения пара, преобразуется в энергию его движения, а остальная часть является потерей полезной работы.

Потерю кинетической энергии или располагаемого теплопере­пада при течении с трением определяют по уравнению:

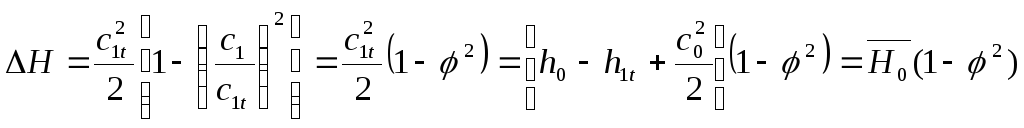. (2.35)

Величину, характеризующую потерю работы из-за действия сил трения, называют коэффициентом потери энергии

(2.36)

откуда потеря располагаемого теплоперепада

_{∆H = ς.} (2.37)

При обтекании паром стенки канала, в частности турбинной лопатки, влияние вязкости, а следовательно, и сил трения обыч­но ограничивается небольшой зоной непосредственно возле стен­ки. Вдали от стенки силы трения можно не учитывать. Очевид­но, и это подтверждается опытами, что скорость потока в этой зоне должна изменяться от нуля на стенке, где поток как бы «прилипает» к ней и полностью заторможен, до скорости в так называемом ядре потока, где влияние сил трения практически не сказывается.

Тонкий, прилегающий к стенке слой потока, в котором ско­рость изменяется от нуля, что соответствует условию прилипа­ния, до значения, соответствующего движению без трения, на­зывают пограничным слоем. Пограничный слой тем тоньше, чем меньше вязкость. Так как внутри пограничного слоя в направле­нии, перпендикулярном движению, скорость изменяется доволь­но быстро, то даже при очень малой вязкости здесь возникают такие силы трения, которые сравнимы с силами инерции и поэ­тому не могут быть отброшены. В то же время вдали от стенок силы трения по сравнению с силами инерции ничтожно малы.

В зависимости от режима течения различают ламинарный и турбулентный пограничные слои. При ламинарном течении слои пара перемещаются параллельно, не перемешиваясь. Турбулент­ное течение сопровождается сильным перемешиванием движущегося пара, в котором наблюдаются пульсации скорости. При­меры распределения скоростей в ламинарном (кривая 1) и тур­булентном (кривая 2) пограничных слоях показаны на рис. 2.5.

Рис. 2.5 Распределение скоростей в ламинарном и турбулентном пограничных слоях

Основным критерием, определяющим влияние вязкости, в част­ности режим (турбулентный или ламинарный) пограничного слоя и его толщину, является безразмер­ное число Рейнольдса, или число Re:

Re = cx/ν, (2.38)

где с — скорость потока, х — характер­ный размер обтекаемого тела (например, хорды лопатки), ν — кинематическая вяз­кость пара.

При решении практических задач для большей части потока вне пограничного слоя используют уравнения движения без учета сил трения (уравнения идеального газа). Зону пограничного слоя рассчиты­вают по полуэмпирическим уравнениям, учитывающим влияние сил трения, кото­рые зависят от числа Re.

Определение размеров сопловых и ра­бочих решеток турбин в основном бази­руется на двух уравнениях: неразрывно­сти и сохранения энергии. Как правило, скорости определяют по уравнениям идеального газа, а силы трения учитывают введе­нием в уравнение неразрывности коэффициента расхода μ.

Сопловые (и рабочие) каналы в турбинах образуются опре­деленным образом установленными лопатками, которые составляют кольцевую сопловую решетку. В турбинах применяют соп­ловые решетки как с полным подводом (рис. 2.6,а), в которых ло­патки расположены по всей окружности, так и с парциальным (рис. 2.6,б), в которых лопатки размещаются только на части окружности. Две соседние лопатки высотой l показаны на рис.2.6, в.

Рис 2.6 Расположение каналов по окружности сопловых решеток с полным (а) и парциальным (б) подводами пара, две соседние лопатки (в), устанав­ливаемые в этих решетках.

Расстояние, на котором располагаются по отношению друг к другу лопатки, образующие канал, называют шагом t решетки (рис. 2.10, в). Если средний диаметр решетки обозначить d, то степень парциальности

, (2.39)

где z — число лопаток (каналов).

Таким образом, как следует из формулы (2.41), степень пар­циальности — это отношение длины дуги, занятой сопловыми ло­патками, к длине окружности, на которой они расположены. Очевидно, что при полном подводе пара степень парциальности е = 1 и произведение шага решетки на число каналов равно дли­не окружности: zt=πd.

Для определения размеров решеток необходимо правильно выбрать соответствующие профили лопаток и рассчитать высоту их выходного сечения. Решетки с дозвуковым течением пара (рис. 2.6, в) имеют площадь выходного сечения, равную произ­ведению ширины минимального сечения а, называемой горлом канала, на высоту l. В таких решетках

^, (2.40)

где α_1э — эффективный (геометрический) угол выхода потока из решетки.

Площадь сопловой решетки определяют по уравнению нераз­рывности

. (2.41)

Удельный объем v_1t и скорость с_1t пара можно определить по изоэнтропному процессу (см. точку D на рис. 2.4). В частности, удельный объем v_1t — по h,s-диаграмме или по уравнению изоэнтропы, а скорость c_1t — по формуле (2.31). Зная площадь на выходе из сопловой решетки

, (2.42)

можно определить высоту лопаток

_. (2.43)

Как уже отмечалось, при дозвуковом течении (ε> ε _*) расширение пара происходит в сужающейся части сопла. При этом давление р₁ в минимальном сечении О - А сопла (рис. 2.7) равно давлению за ним.

Рис. 2.7 Расширение пара в косом срезе сопла

Критическую скорость за соплом с_кр = а получают в сечении О - А при отношении давлений, равно­му критическому ε = ε_* . В дозвуковом потоке (ε >=ε_*) косой срез сопла ОАВО служит только для направления потока пара под углом α_1э .

В сверхзвуковом потоке (ε ‹ ε _*) расширение пара до критического давления p_кр также происходит в суживающейся части сопла. При этом в сечении О—А сопла устанавливается критическая скорость пара, а его дальнейшее расширение от р_кр до р₁ происходит в косом срезе ОАВО. В этом случае поток перестает быть симметричным относительно оси сопла.

Для выяснения явлений, происходящих в косом срезе, рас­смотрим отдельные струйки потока. Часть потока у кромки в точке О попадает из области с давлением р_кр в сечении ОА в камеру за соплом с давлением p₁<р_кр. Расширение пара проис­ходит в камере за соплом от давления р_кр до р₁. Часть потока у поверхно­сти лопатки АВ расширя­ется от давления р_кр до давления в точке В так же, как в сопле Лаваля, т. е. по мере движения потока давление посте­пенно снижается от p_кр до р₁. При этом тепловая энергия потока преобра­зуется в кинетическую (поток ускоряется).

Соединив точки с оди­наковыми давлениями, по­лучим пучок изогнутых изобар, которые собираются в точке О, где давление резко изме­няется от р_кр до р₁.

В сверхзвуковом потоке, как отмечалось, пло­щадь сечения струи в соответствии с уравнением неразрывности должна увеличиваться. Поскольку в косом срезе сопла поток па­ра ограничен только с одной стороны поверхностью АВ, увели­чение его площади возможно лишь при увеличении угла поворо­та от α_1э до α_1Э+δ. Угол отклонения потока δ можно рассчитать следующим образом.

Расходы пара в сечениях О—А и В—С одинаковы и состав­ляют

, (2.44)

где F_min и F₁ — площади в сечениях О - А и В - С.

При одинаковой высоте решетки в сечениях О - А и В - С их площади прямо пропорциональны ширине сопла:

. (2.45)

Из треугольников ОАВ и ОВС определим

и . (2.46)

П

(2.47)

о формулам (2.46), (2.47) и (2.48) можно определить угол вы­хода потока из сопла

.

Зная угол выхода сверхзвукового потока из сопловой решет­ки, можно по формуле (2.43) определить ее высоту l₁ .