Тема 3. Случайные величины

1. р_i=Р(Х=х_i).

хi	х1	х2	…	хn
рi	р1	р2	…	рn

3. 1) 0≤Р(х) ≤1

2) ∑ Р(х) = 1 (или∑p_i=1)

4. F(x)=P(X≤x)=

5.

Р 1 … р2 р1 х1 х2…..хn х

6. Свойства функции распределения:

1) 0 ≤ F(х) ≤ 1

2) если .

3) F(x-0)=F(x).

4)

7. Операции над случайными величинами.

1) сХ, (cx₁, cx₂, ...,сх_n )

2) X² (x₁²,x²₂,...,x_n² )

3) X±Y ( x_i±y_j (i=l,2,...,n; j=l,2, ...,m))

4) XY ( x_i*y_j (i=l,2,...,n; j=l,2, ...,m))

8.

9. Свойства математического ожидания

1) М(с)=с

2) М(сХ)=сМ(Х), где с – константа.

3) M(X Y)=M(X) M(Y)

4) M(XY)=M(X)M(Y)

5) М(Х с)=М(Х) с

Следствие. М[Х-М(Х)]=0

6) М(Х)=М(Х_i).

10.

11. Свойства дисперсии

1) D(c)=0

2) D(cX)=c²D(X)

3) D(X±Y)=D(X)+D(Y)

4) n σ²,

σ²/n ,

т.е. D(X)=σ²/n

12. σ²=D(X)=M(X²)–[M(X)]², где

13.

14. F(x) = Р(Х < х).

15. P(α<x<β) = F(β) - F(α).

16.

F(x) F(x)=1 1 F(x)=0 x

17. f(x)=F`(x).

18. Свойства дифференциальной функции f(x)

1) f(x)≥0.

2)

19.

20.

21.

22.

23. σ²=D(X)=M(X²)–[M(X)]², где

24.

ДСВ	НСВ

25.

ДСВ	НСВ

Тема 4. Законы распределения случайных величин.

1. Биномиальное распределение.

X=m	0	1	2	…	m	…	n
Рn,m				…		…

М(Х)=nр, σ²=D(X)=npq, .

2. Распределение Пуассона.

,

X=m	0	1	2	…	m	…	n
Рn,m				…		…

3. Гипергеометрическое распределение

N

М N-M

n

m m

X=m	0	1	2	…	m	…	n
Рn,m				…		…

,

4. Равномерное распределение.

1)

2)

f(x) c 0 a b x

F(x) 1 0 a b x

3)

4)

5)

5. Нормальное распределение

1)

2) М(х)=а.

3) D(х) = σ²,

4)

5)

6)

f(x) а х

7)

8)

f(x) а - σ а а + σ х

9)

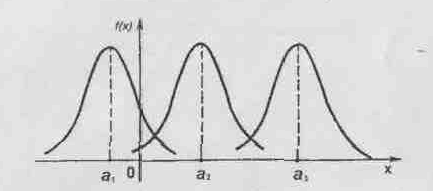
10)

11)

12)

φо(х) 0,3989 0 х

13) .

14) Х N(а; σ),

15)

F (x)

1

0,5

а х

16) Функция Лапласа Ф_о(х)

17)

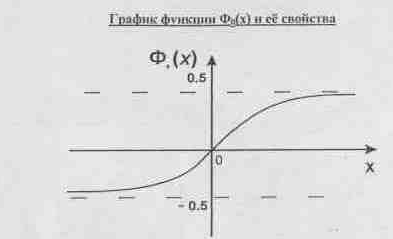
18)

19) P(α<X<β)=F(β) - F(α)

20) P(α<X<β)=0,5+Ф₀ -0,5-Ф₀ = Ф₀ - Ф₀

21)

22) P(|Х -а|< tδ)≈2Ф₀ (t).

23)

t = 1 → Р(|Х - а| <σ) ≈2Ф₀(1) ≈ 0,6827

t = 2 → P(|Х - а| < 2σ) ≈ 2Ф₀(2) ≈0,9545

t = 3 → P(|X - а|) < 3σ) ≈2Ф₀(3) ≈ 0,9973

24) а - 3σ < X < а + 3σ