Билет n7

1.Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Момент инерции определяется как I=∑m_iR_i²

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

Ось, положение которой в пространстве остается неизменным при вращении вокруг нее тела в отсутствие внешних сил, называется свободной осью тела.

для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями: они называются главными осями инерции.

У тела, обладающего осевой симметрией (например, у однородного цилиндра), одной из главных осей инерции является ось симметрии, в качестве двух других осей могут служить две любые взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной к оси симметрии и проходящие через центр инерции тела. Таким образом, у тела с осевой симметрией фиксирована только одна из главных осей инерции.

Моменты инерции относительно главных осей называются главными моментами инерции тела. В общем случае эти моменты различны. Для тела с осевой симметрией два главных момента имеют одинаковую величину, третий же, отличен от них. В случае тела с центральной симметрией все три главных момента инерции одинаковы.

Теоре́ма Ште́йнера: момент инерции J тела относительно произвольной оси равен сумме момента инерции этого тела J_c относительно параллельной ей оси, проходящей через центр масс тела , и произведения массы тела m на квадрат расстояния d между осями:

J=J_c+md²

где

J_c — известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси,

m — масса тела,

d — расстояние между указанными осями.

2. РАСПРЕДЕЛЕНИЕ БОЗЕ-ЭЙНШТЕЙНА - функция распределения по уровням энергии тождеств. частиц с нулевым или целочисленным спином при условии, что взаимодействие частиц слабое и ими можно пренебречь, т. е. функция распределения идеального квантового газа, подчиняющегося Бозе - Эйнштейна статистике.

РАСПРЕДЕЛЕНИЕ БОЗЕ-ЭЙНШТЕЙНА соответствует максимуму статистического веса (или энтропии) с учётом неразличимости частиц, отвечающей требованиям БОЗЕ-ЭЙНШТЕЙНА -статистики. При темп-ре ниже темп-ры вырождения БОЗЕ-ЭЙНШТЕЙНА -газ испытывает Бозе - Эйнштейна конденсацию, при к-рой часть частиц Скапливается в состоянии с нулевым импульсом, а остальные частицы распределены согласно распределению БОЗЕ-ЭЙНШТЕЙНА

В квантовой теории вероятность заполнения энергетических состояний электронами определяется функцией распределения Ферми- Дирака:

f(W,T)=1/(1+exp((W-W_f)/kT))

где W - энергия уровня, вероятность заполнения которого определяется при температуре T; k - постоянная Больцмана.

3. 7.Задача: В баллоне находилось 10кг газа при давлении 10⁷н/м² Найти какое количество газа взяли из баллона, если окончательное давление стало равным 2,5 10·⁶н/м² Температуру считать постоянной. => ; => = ;
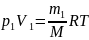
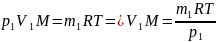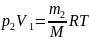
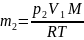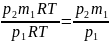