Экзаменационный билет №17.

1.Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Резонанс.

Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.

Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.

(1)

Решение уравнения (1) запишем в виде   (2)  где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем   (3)  Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента:   (4)  (если (ω₀² - σ²)>0, то такое обозначение мы вправе сделать). Тогда получим выражение   , у которого решение будет функция   . Значит, решение уравнения (1) в случае малых затуханий (ω₀² >> σ² )   (5)  где   (6) — амплитуда затухающих колебаний, а А₀ — начальная амплитуда. 

Резонанс

При частоте вынуждающей силы, равной частоте свободных колебаний, возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем

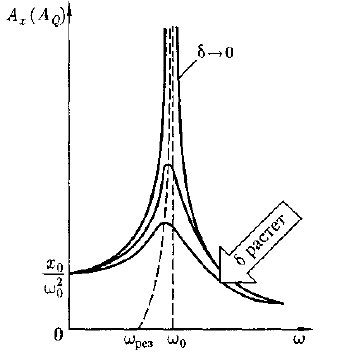
Колебания в резонансе будут описываться следующим соотношением: График резонансных кривых:

2.Диффузия. Закон Фика. Коэффициент диффузии.

Диффу́зия- процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму.

Перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией.

Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной)

первый закон Фика :

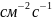
показывает, что плотность потока вещества J ( ) пропорциональна коэффициенту диффузии D (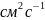 ) и градиенту концентрации

второй закон Фика:

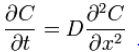
Коэффициент диффузии D зависит от температуры

Билет n18

1.Стоячая волна — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

В одномерном случае две волны одинаковой частоты, длины волны и амплитуды, распространяющиеся в противоположных направлениях (например, навстречу друг другу), будут взаимодействовать, в результате чего может возникнуть стоячая волна. Например, гармоничная волна, распространяясь вправо, достигая конца струны, производит стоячую волну. Волна, что отражается от конца, должна иметь такую ​​же амплитуду и частоту, как и падающая волна.

Рассмотрим падающую и отраженную волны в виде:

y₁=y₀sin(kx-wt) y₂=y₀*sin(kx+wt)

где y₀ –амплитуда волн, w -циклическая (угловая) частота, измеряемая в радианах в секунду,

k -волновой вектор, измеряется в радианах на метр, и рассчитывается как 2π поделённое на длину волны,

Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y1 и y2:

y=2y₀cos(wt)sin(kx)

В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

u=u₀cos(kx)cos(wt-ϕ)

где u — возмущения в точке х в момент времени t, u₀ — амплитуда стоячей волны, w— частота , k — волновой вектор, — ϕ фаза.

2. Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:

Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получаем PV 3 – (RT + bP) vV 2 + av2V - abv3 = 0.

Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке. Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Ткр, которая разделяет немонотонные T < Tкр и монотонные T > Ткр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Ткр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермы Т1 давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLB и AGE давление падает с увеличением объема (dP/dV)Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD (жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL.

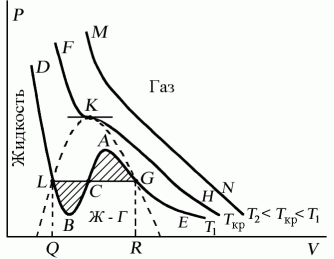При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.

Наличие критической точки на изотерме Ван–дер–Ваальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии. Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна