41. Для системы

- записать векторно-матричное дифференциальное уравнение

- найти W_му(p)

- найти Ф(t)

- найти H_y(t)

(б10)

Векторно-матричные уравнения

; ; ; ;

Составим элементы переходной матрицы

, Подавая 2 на 2 мы имеем разомкнутую систему, тогда составим уравнение для замкнутой системы , по лаппласу , тогда , преобразуя по Лапласу получаем e^-2t.

Тогда ;

Резольвента

Передаточ. Ф-я

Матрич. перех. ф-я:

42. Для системы

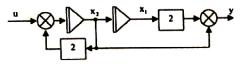
- записать векторно-матричное дифференциальное уравнение

- найти W_му(p)

- найти Ф(t)

- найти H_y(t)

(б11)

; ; ; ;

Составим элементы переходной матрицы

, Подавая 2 на 2 мы имеем разомкнутую систему, тогда составим уравнение для замкнутой системы , по Лапласу , тогда , преобразуя по Лапласу получаем e^2t.

Тогда ;

Резольвента

Передаточ. Ф-я

Матрич. перех. ф-я:

43. Собственные числа. Левые и правые собственные числа. Аналитическая функция от матриц.(б12).

Умножение квадратной матрицы на нек век дает новый век , который, в общ случае, иначе ориентирован в про­странстве и имеет другую длину по сравнению с исходным вектором. Но есть такие векторы, кот при вып этой опе­рац мен только свою длину, но не меняют направления, то есть

(2.4.1) где - вещественная или комплексная скалярная величина, назы­ваемая собственным значением (характеристическим числом) матрицы , а вектор - собственный вектор этой матрицы. В развёрну­том виде уравнение (2.4.1) имеет следующий вид:

.Очевидно, что для существования ненулевых необходимо вы­пол­не­ние условия

. (2.4.2) Это уравнение называют характеристическим, или вековым уравнением матрицы . Левая часть этого уравнения называется характеристичес­ким полиномом, степень его равна размеру n матрицы : .(2.4.3).

Таким образом, каждая квадратная матрица

имеет собственных зна­чений , которые могут быть определены путём решения характеристического уравнения с использованием стандартного матема­тического обеспечения на цифровых вычислительных машинах.

Алгебраическая кратность корня – это его кратность как корня характеристического уравнения. Геометрическая кратность корня – это количество линейно независимых векторов , связанных с данным .

Собственные значения транспонированной матрицы - это такие , для которых система уравнений (2.4.7) имеет нетривиальные решения, т.е. когда .(2.4.8) Решение этого алгебраического уравнения дает значений собственных чисел . Так как определители квадратной матрицы и её транспонированной матрицы равны, то собственные числа матриц и также равны. Таким образом, собственному числу соответствует собственный вектор матрицы и собственный вектор матрицы . Если транспонировать обе части уравнения (2.4.7), то получим .(2.4.9) В связи с этим вектор называют левым собственным вектором матрицы , в отличие от , который, в таком случае, называют правым собственным вектором. Для -го собственного числа и -го левого собственного вектора соответственно

68. Для объекта с управлением u=50v-(48 7) построить наблюдатель полного порядка (б14).

1. Запишем матрицы в исходном базисе: ; ; ; N;

A=A_н , В=В_н , С=С_н;

2. Характеристический полином матрицы А его коэффициенты и нули: α₁=3, α₂=2, λ₁=-1, λ₂=-2;

3. t_рег определяется наиболее близким к оси коэффициентом c. (λ- λ₁)( λ- λ₂); его коэффициенты

Задаем собственные числа λ_1н=λ_2н=-3; Вычисляем характеристический полином и . (вычисли сам)

4. Определить матрицу перехода в ИКП: ; ; N=

Учитывая преобразование в базисе ИКП 5.Матрица перехода от исходного базиса к ИКП f_н =

6. Получим матрицу в исходном базисе K_н f_н = , ; ;