2.6. Учет инфляционного обесценения денег в принятии финансовых решений

Инфляция характеризуется обесценением национальной валю- ты (т. е. снижением ее покупательной способности) и общим по- вышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесце- нения денежных средств, то заемщик может получить возмож- ность погасить задолженность деньгами сниженной покупатель- ной способности.

Во избежание ошибок и потерь в условиях снижения покупа- тельной способности денег рассмотрим механизм влияния ин- фляции на результат финансовых операций и проведем неслож- ные математические расчеты и преобразования.

Пусть S_a — сумма, покупательная способность которой с уче- том инфляции равна покупательной способности суммы при от- сутствии инфляции. Через AS обозначим разницу между этими суммами.

Отношение AS /S₉ выраженное в процентах, называется уров- нем инфляции.

При расчетах используют относительную величину уровня ин- фляции — темп инфляции а.

109

Тогда для определения S_a получаем следующее выражение:

(6.1)

Величину (1 + а), показывающую, во сколько раз S_a больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции /_и .

(6.2)

Динамика индекса инфляции за несколько лет отражает изме- нения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по срав- нению с предыдущим таким же периодом указывает на ускорение инфляции, снижение — на уменьшение ее темпов.

Пусть а — годовой уровень инфляции. Это значит, что через год сумма S'_a будет больше суммы S в (1 + а) раз. По прошествии еще одного года сумма S^ будет больше суммы S'_a в (1 + а) раз, т. е. больше суммы Sb (1 + а)² раз. Через п лет сумма S£ вырастет

по отношению к сумме 5в (1 + а)^п раз. Отсюда видно, что инфля- ционный рост суммы S при годовом уровне инфляции а — то же самое, что наращение суммы S по сложной годовой ставке про- центов а.

Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.).

Очень важно запомнить данную аналогию со сложным процентом, так как одна из наиболее часто встречающихся ошибок, связанных с расчетом уров- ня инфляции за некоторый период, связана именно с не- учетом данного обстоятельства.

Например, если цены каждый месяц растут на 2%, то за годовой уровень инфляции, недолго думая, принимают 2% • 12 = 24%. Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 25% годовых. Между тем, если уровень инфляции составляет 2% в месяц, это значит, что за месяц цены вырастают в (1 + 0,02) = 1,02 раза, а за год — в 1,02¹² = 1,268 раза. Значит годовой темп инфляции со- ставляет 1,268 - 1 = 0,268, т. е. годовой уровень инфляции достигает 26,8%. После такого расчета процентная ставка 25% годовых теряет свою инвестиционную привлекатель- ность и может рассматриваться лишь в плане минимиза- ции потерь от инфляции.

по

Рассмотрим теперь различные случаи задания уровня инфля- ции.

Если известен годовой уровень инфляции а, то за период в п лет (при том, что п = п_а + п_ь и п_а — целое число лет, п_ь — остав- шаяся нецелая часть года) индекс инфляции, очевидно, составит следующую величину:

(6.3)

В некоторых случаях может быть задан уровень инфляции а_т за короткий (меньше года) интервал. Тогда за период, составляю- щий т таких интервалов, индекс инфляции будет равен

(6.4)

Теперь можно приложить изложенные в предыдущих па- раграфах варианты начисления процентов к условиям инфляци- онной экономики.

Если в обычном случае первоначальная сумма P при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму S_a, что требует уже иной процентной ставки.

Назовем ее ставкой процентов, учитывающей инфляцию.

Пусть

• ставка ссудного процента, учитывающая инфляцию;

• учетная ставка, учитывающая инфляцию;

• номинальная ставка сложного процента, учитываю- щая инфляцию;

— номинальная сложная учетная ставка, учитывающая инфляцию.

Зададим годовой уровень инфляции а и простую годовую став- ку ссудного процента /. Тогда для наращенной суммы S, превра- щающейся в условиях инфляции в сумму S_a, используем формулу (1-7):

Для данной суммы можно записать еще одно соотношение:

а затем составить уравнение эквивалентности:

ill

из которого следует, что

(6.5)

Мы получили, таким образом, известную формулу И. Фишера, в которой сумма (а + /а) является величиной, которую необходи- мо прибавить к реальной ставке доходности для компенсации ин- фляционных потерь. Эта величина называется инфляционной премией.

Зная формулу И. Фишера, можно избежать еще одной распространенной ошибки. Часто для под- счета процентной ставки, учитывающей инфляцию, к вели- чине реальной ставки доходности просто прибавляют ве- личину темпа инфляции, т. е. если / = 25% и а = 15%, то за процентную ставку, учитывающую инфляцию, принимается сумма (/ + а) = 25 + 15 = 40%. Но нужно помнить, что суще- ствует еще произведение (/ а), величина которого тем больше, чем больше значения / и а. В нашем примере оно составляет 0,15 • 0,25 = 0,0375 = 3,75%. Наверное не стоит пренебрегать даже такой, на первый взгляд, небольшой величиной. Ведь когда счет идет на десятки миллионов, каждый процентный пункт — это сотни тысяч рублей.

Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значени- ем индекса инфляции за весь рассматриваемый период.

Для простых процентных ставок по формуле (1.7) получаем

В то же время должно выполняться равенство:

Составим уравнение эквивалентности:

из которого получаем

(6.6)

Для простых учетных ставок аналогичное уравнение эквива- лентности будет иметь вид:

112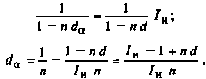

(6.7)

Для случая сложных процентов используем формулу (3.1):

Отсюда

(6.8)

Если начисление процентов происходит несколько (/и) раз в го- ду, используем формулу (3.6):

Отсюда

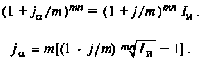(6.9)

Таким же образом получаем две формулы для случая сложных учетных ставок:

(6.10)

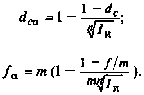(6.П)

Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность фи- нансовой операции, и уровень инфляции в течение рассматри- ваемого периода. Эти формулы можно преобразовать и получить зависимость / от /_а или любую другую. Например, из формулы (6.6) можно получить формулу, позволяющую определить реаль- ную доходность финансовой операции, когда задан уровень ин- фляции и простая ставка процентов, учитывающая инфляцию:

(6.12)

Из формулы (6.8) получаем аналогичную формулу для случая сложных процентов:

(6.13)

Подставив в последнюю формулу вместо индекса инфляции выражение получим простую формулу:

(6.14)

отражающую несколько очевидных соображений:

из

если i_ca = а (доходность вложений и уровень инфляции рав- ны), то /_с = 0, т. е. весь доход поглощается инфляцией;

если i_ca < а (доходность вложений ниже уровня инфляции), то /_с < 0, т. е. операция приносит убыток;

если /_са > а (доходность вложений выше уровня инфляции), то i_c > 0, т. е. происходит реальный прирост вложенного капитала.

Пример 22

Кредит в размере 50 000 000 руб. выдан на два года. Реальная доходность операции должна составить 10% годовых по сложной ставке ссудного процента. Ожидаемый уровень инфляции состав- ляет 15% в год. Определить множитель наращения, сложную став- ку процентов, учитывающую инфляцию, и наращенную сумму.

Решение

По формуле (6.3) получаем

I₁₁ = (I +0,15)²= 1,3225.

Множитель наращения и номинальная ставка доходности рав- ны:

Далее для наращенной суммы получаем

Пример 23

Первоначальный капитал в размере 20 000 000 руб. выдается на три года, проценты начисляются в конце каждого квартала по но- минальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожи- даемый годовой уровень инфляции составляет 12%. Решение Воспользуемся формулой (6.3):

/_и = (1 +0,12)³=1,4. По формуле (6.9) имеем

j_a= [(I + 0,08/4) ¹^M - 1] 4 = 0,107 = 10,7%. Отсюда

S = 20 000 000 (1 + 0,107/4)¹² = 27 454 048 (руб.).

Пример 24

При выдаче кредита должна быть обеспечена реальная доход- ность операции, определяемая учетной ставкой 5% годовых. Кре-

дит выдается на полгода, за которые предполагаемый индекс ин- фляции составит 1,06. Рассчитать значение учетной ставки, ком- пенсирующей потери от инфляции.

Решение

Производим вычисления по формуле (6.7):

Пример 25

Определить реальную доходность финансовой операции, если при уровне инфляции 0,9% в месяц выдается кредит на два года по номинальной ставке сложных процентов 15% годовых. Про- центы начисляются ежеквартально.

Решение

Принимая заданную номинальную процентную ставку за став- ку, учитывающую инфляцию, получим из формулы (6.9) соотно- шение для определения реальной номинальной ставки сложных процентов:

(6.15)

По формуле (6.4):

Отсюда

Пример 26

Определить, какой реальной убыточностью обладает финансо- вая операция, если при уровне инфляции 14% в год капитал вкла- дывается на один год под номинальную ставку 8% при еже- месячном начислении.

Решение

Находим сначала индекс инфляции:

Далее используем формулу (6.15):

Таким образом, данная операция будет приносить 5,1%-ный убыток.

115