71.Кривизна поверхні і додатковий тиск . Формула Лапласа . Капілярні явища

Якщо поверхня рідини-крива , то при рівновазі тиски по різні її сторони повинні бути різними . Явище обумовлено силами поверхневого натягу. Розглянемо випадок коли рідина

о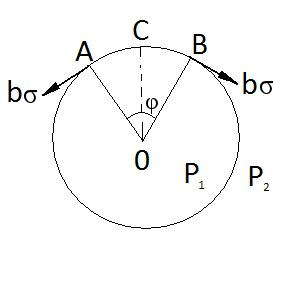 бмежена циліндром: 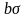- дотичні сили ,b - довжина циліндра рівнодіюча сила:

або 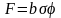, , 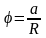де а- довжина дуги, отримаєм

, де S=аb . Розділивши Силу F на площу S знайдемо різницю тисків всередині і назовні рідини

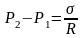
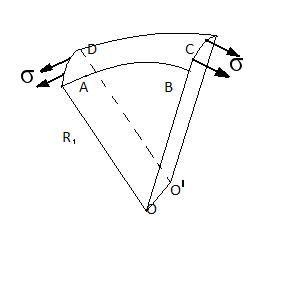. 2. Узагальнимо цю формулу на випадок ,коли рідина обмежена поверхнею подвійної кривизни

Тоді 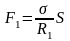, де S –площа ABCD

Результуюча дотичних сил рівна

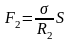, де R2 , радіус AD

Результуюча всіх сил поверхневого натягу рівна:

Розділивши її на S отримаємо різницю. Тисків - формула Лапласа.

3. Якщо розміри посудин, в яких знаходиться рідина, або відстань між поверхнями , обмежуючих рідину , порівняні з радіусом кривизни поверхні рідини , то такі посудини називають капілярними , а явища , протікаючи в посудині, називають капілярними явищами .

В таких посудинах характерна дія додаткового тиску (тиск Лапласа),за допомогою якого відбувається явище капілярного підйому, а величина на яку підіймається рідина визначається за формулою: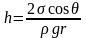

72.Капілярно-гравітаційні хвилі. (Доведення)

У випадку, коли одночасно діють сили тяжіння і сили поверхневого натягу, хвилі називаються гравітаційно-капілярними. Вплив сил поверхневого натягу найбільший при малих довжинах хвиль, сил тяжіння – при більших. Швидкість 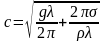розповсюдження хвиль на поверхні рідини залежить від довжини хвилі . При  довжини хвилі швидкість розповсюдження гравітаційно-капілярних хвиль спочатку  до деякого мінімального значення 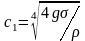, а потім  ( - поверхневий натяг, g – прискорення вільного падіння,  - густина рідини). Значенню с₁ відповідає довжина хвилі 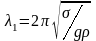. При  > ₁ швидкість розповсюдження залежить переважно від сил тяжіння і не залежить від поверхневого натягу, тоді дані хвилі називаються гравітаційними, а при  < ₁ – від сил поверхневого натягу, де 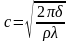. Для поверхні розділу води і повітря ₁=1,71 см. Причини виникнення гравітаційних хвиль: притягання рідини Сонцем і Місяцем, рух тіл поблизу або на поверхні води (пароплавні хвилі), дія на поверхні рідини системи імпульсних тисків

(місцеве підвищення рівня при підводному вибуху).

А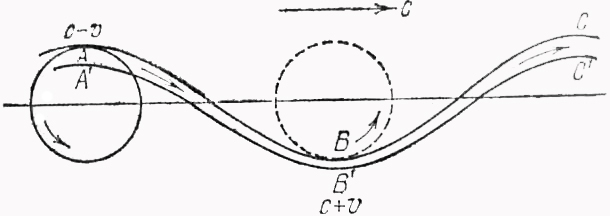 ВС-представляє траєкторію частинки на поверхні рідини. А’В’С’-безкінечно близька до неї частинки в глибині рідини.

-швидкість руху рідини в околі. -швидкість рідини в точці А. 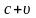-повна швидкість в точці В. Різниця висот точок А та В дорівнює h=2r. З рівняння Бенуллі:

або

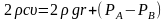
Видно: 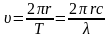. Тиск рідини в точках А та В по формулі Лапласа рівні: 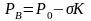, де К– абсолютне значення кривизни в точці А або В.

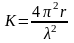
.Звідси

73.Кристалічний та аморфний стан речовини.

Належність речовини до кристалічного або аморфного стану визначається взаємним розташуванням атомів у ній.

У кристалічній речовині атоми розташовані впорядковано. Певний структурний елемент стало повторюється, утворюючи кристалічну структуру.

Атомна структура називається ідеальним кристалом, якщо в ній є три некомпланарних вектори a1,a2,a3, що утворюють праву трійку, при зсуві на кожний з яких вона не змінюється, тобто інварінтна. Зсув на кожний з таких векторів називається трансляцією.

Обєм паралелепіпеда, побудованого на цих векторах, буде дорівнювати мішаному добутку базових векторів, який можна записат як Ω=a1ּ۬[a2xa3]=a2ּ[a3xa1]=a3ּ[a1xa2] (1) Якщо вектори a1,a2,a3 вибрані таким чином, що обєм паралелепіпеда Ω має мінімально можливе значення, то ці вектори називають трансляційними або основними векторами трансляції, а побудований на них паралелепіпед-елементарною коміркою кристала. Якщо відомі основні вектори трансляції, можна знайти сукупність точок r’=r+n1a1+n2a2+n3a3, де r-довільна точка, а n(1,2,3)- довільні цілі числа(додатні відємні та нуль). Ця сукупність точок при довільних значеннях n утворює кристалічну гратку, самі точки мають назву вузлів кристалічної гратки. Кристалічна гратка є результатом усіх можливих трансляцій елементарної комірки і є сама по собі математичною абстракцією. Кристалічна структура утворюється лише тоді, коли з кожним вузлам гратки однаковим чином пов'язаний певний базис. Базисом може бути довільна сукупність атомів чи молекул, але завжди однакова біля кожного вузла. Головна асобливість внутрішньої будови тіл, що знаходяться у аморфному стані,- відсутність дальнього порядку, тобто характерної для кристалів повторюваності одного й того ж елементу структури. У аморфних речовин існує так званий ближній порядок, тобто деяка узгодженість у розташуванні у просторі сусідніх атомів, яка зникає із збільшенням відстані від вибраного атома.

Такі особливості розташування атомів зумовлюють фізичні властивості кристалів і аморфних тіл:

1. Кристалічні тіла анізотропні, чого повністю позбавлені аморфні тіла. Але анізотропію властивостей можна експериментально зафіксувати лише на дуже досконалих монокристалах. Найчастіше досліджуються полікристалічні речовини, де окремі монокристали розташовані в просторі хаотично. Тому, хоч кожний монокристал є анізотропним, полікристал буде ізотропним.

2. Кристали мають правильну геометричну форму. У всіх кристалах даної речовини за однакових умов кути між відповідними гранями кристалів однакові. Це закон сталості кутів кристалу, встановлений Стеноном у 1669 році на основі спостережень над багатогранними кристалами у природі.

3. Кристали, на відміну від аморфних тіл, розколюються вздовж певних площин.

4. Кристали, на відміну від аморфних тіл, мають фіксовану температуру плавлення.

5. І, найголовнішу, кристали мають стійку симетрію

Елементи симетрії кристалів

Симетрія-це властивість тіла суміщатися із самим собою під час деяких операцій або перетворень. Трансляційна симетрія є операцією, коли зсув всієї нескінчнної кристалічної гратки на основні вектори трансляції суміщає її із собою.

Наступні елементи симетрії мають назву точкових, оскільки при операції хоча б одна точка не змінює свого положення. При цьому, якщо трансляційна симетрія обовязкова для будь-якого кристала, ці елементи симетрії не є обовязковим атрибутом кожного кристала.

Вісь симетрії n-го порядку. Пряма, що проходить в кристалі, називається його віссю симетрії n-го порядку, якщо тіло суміщається із собою при вороті навколо цієї прямої на кут 360/n . кристал може мати осі симетрії 1,2,3,4 і 6-го порядків.

Дзеркальна площина. Якщо відображення від якоїсь площини переводить кожний вузол гратки в його дзеркальне зображення, то площина називається дзеркальною.

Центр інверсії. Нехай є деяка точка, від якої м ибудемо відраховувати радіус вектор r(x,y,z). Якщо тіло інваріантне операції r(x,y,z)=- r(-x,-y,-z) то точка відліку називається ценром інверсії.

Інверсійна вісь n-го порядку. Тіло суміститься із собою при повороті на кут 360/n навколо своєї осі і наступної інверсії щодо вузла, що лежить на цій осі.

Дзеркально-поворотна вісь n-го порядку. Тіло суміститься із собою при повороті навколо осі на кут 360/n і наступному дзеркальному відображенні в площині, перпендикулярній цій осі.

Сукупність точкових елементів симетрії, які має тіло, називається його точковою групою симетрії. Якщо до цих елементів чиметрії додати ще елементи симетрії, при яких жодна точка тіла не залишається нерухомою, наприклад, при трансляції на вектори гратки, то ми отримаємо просторову групу симетрії. Симетрія покладена в основу класифікації кристалів.