69.Явище поверхневого натягу

Рідкий стан утворюється тоді, коли потенціальна енергія притяжіння молекул переважає над їх потенціальною енергією. Таким чином у рідин утворюється поверхність, котра обмежує її об`єм. На частини, котрі знаходяться поблизу поверхні, діють зі сторони інших молекул рідини сили, рівнодійна яких, направлена в середину рідини нормально до поверхні. Для збільшення поверхні рідини потрібно виконати роботу. При Т=const роль потенціальної енергії грає вільна енергія Е, для якої правдиве відношення dE=-dA? Де dA – робота, пов’язана з виникненням вільної енергії. В результаті однорідності поверхні вільна енергія ~ S(площі). Тому E=s , де  -питома густина вільної енергії поверхні. Так як і в механіці, система прямує до мінімальної потенціальної енергії. В термодинаміці система прямує до мінімуму вільної енергії. Тому поверхня рідини намагається скоротитись. Завдяки цьому вздовж поверхні рідини діють сили , котрі називаються силами поверхневого натягу.

Робота, яку треба виконати щоб ізотермічно, квазістатично збільшити поверхню рідини на одиницю, при незмінному об`ємі, називається коефіцієнтом поверхневого натягу, або поверхневим натягом.

dF=-SdT – pdV (SdT=0)

dF=-pdV=-δA

F=Fоб+ Fпов

f1=f(V) f1-обємна густина вільної енергії

Fпов=(f2)a

f2=  - коефіцієнт поверхневого натягу

δQ=dU+δA dA TdS=dU- da da F=U-TS -da dF=dU-TdS-SdT dU-TdS=da dF=da-SdT - Зміна вільної енергії при зміні площі поверхні на одиницю S= U=F-T U=F-T F= a

U= a-T a ∆Q=∆U-∆ a ∆Q=∆ a-T a-∆ a=-T ∆ a q= =-T

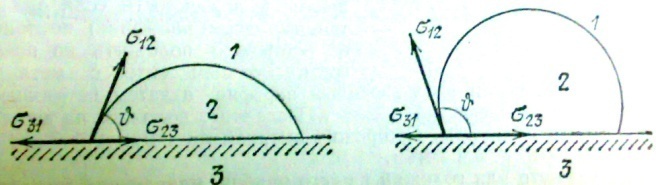
70. Крайові кути.Змочування.Умови рівноваги на межі трьох рідин та на межі рідини з іншим середовищем.

Припустимо три рідких середовища(1,2,3)попарно межують для рівноваги потрібно,щоб всі сили,які діють на рідину всередині циліндра S,урівноважувались.Ці сили складаються з сил поверхневого натягу ,сил гідростатичного тискуна поверхність S та сили тяжіння рідини,замкненої всередині об’єму, обмеженого даною поверхнею.Силою тяжіння і гідростатичним тиском можна знехтувати і записати відповідне рівняння: (2)з собою вздовж трьох поверхонь,які перетинаються вздовж деякої лінії О.Приклад:крапля на поверхні іншої рідини.(мал)При цьому векторна умова рівноваги (2) розпадається на два скалярних рівняння:

;

З них отримуємо: ;

Цими формулами визнач. кути . Рівновага можлива ,коли < + .якщо остання умова не виконується,то не існує кутів ,які б задовольняли умову(4)При цьому капля розтікається по поверхні рідини.В даному випадку кажуть,що рідина 3 повністю змочується рідиною 2.

Аналогічна ситуація,з каплею на твердому тілі. Різниця в тому,що тверда поверхня не може деформуватися. Кут визначається з формули:

;

Кут θ називається крайовим кутом. Зазвичай його обирають так,щоб він включав в себе область зайняту рідиною2.Коли >1, > + .

Але тоді не виконується умова cosθ= .Капля рідини не знаходиться в рівновазі,а ростікається по поверхні твердого тіла,покриваючи її тонкою плівкою.В цьому випадку говорять,що рідина повністю змочує поверхню твердого тіла. В іншому випадку

<-1,то також не існує ніякого кута θ,який би задовольняв умову(1). Рідина в цьому випадку зтягується в сферичну каплю,дещо приплюснутою силою тяжіння. В цьому випадку кажуть,що капля не змочує поверхність твердого тіла.В більшості випадків має місце частичне змочування.