63. Рівняння Ван-дер-Вальса. Їзотерми Ван-дер-Вальса. Взаємні перетворення пари та рідини.

Р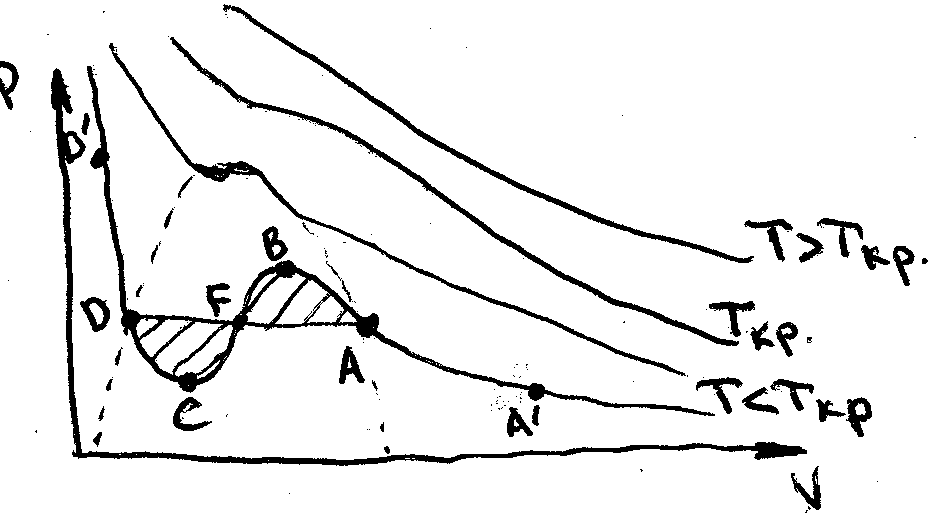 івняння називається рівнянням стану реального газу, або рівнянням Ван-дер-Ваальса. Поправки a і b називаються сталими Ван-дер-Ваальса і залежать від природи газу. Це рівняння описує стан одного моля реального газу. Якщо розглядати довільну кількість газу масою , то рівняння можна переписати так: . Доданок в перших дужках враховує взаємодію молекул газу, а в других – розміри молекул. Порівнюючи рівняння Ван-дер-Ваальса з рівнянням стану ідеального газу ( ), приходимо до висновку, що ізотерми реального газу відрізняються від ізотерм ідеального. Типові ізотерми Ван-дер-Ваальса наведено на рис. Кожному значенню тиску відповідає одне або три значення об‘єму (в ідеальному газі тільки одне). Оскільки рівняння Ван-дер-Ваальса для реального газу є многочленом 3 степення відносно V, то для різних P при T=const буде 1 або 3 різні значення V. Експериментальні ізотерми T>Tкр збігаються з теор. А при T<Tкр є деякі відмінності. На CB тиск (P) росте із ростом об’єму (V) Ясно, що ні в одній точці система не може бути в рівновазі. Тому CB існує не стійко. В областях D’DC і BAA’ . Тому ці стани стійкі. Отже, цікаво, як може система перейти з однієї області в іншу через нестійку область. Експеримент показав,що на цьому етапі ізотерма в натурі горизонтальна DA. Перейдемо з D в A оборотньо двома шляхами – DFA і DCFBA.

Тоді: , оск. T1=const , Отже DFA повинна бути так розміщена, щоб а отже відповідні площі під кривими DFA і DCBA повинні бути однакові. Ясно, що A’A і DD’ – газоподібний та рідкий стани. На AB і CD відповідно – переохолоджена пара та перегріта рідина. Ці стани метастабільні, тобто нестійкі. Переохолоджена пара – це стан речовини коли по параметрам має бути рідина але є газ (має властивості газу – заповнює весь об’єм і т.д. ), а перегріта рідина відповідно – коли по параметрам має бути газ а є рідина (по властивостям).

64.Критичний стан. Критичні параметри. Методи визначення критичних параметрів. Зведене рівняння Ван-дер-Вальса.

При певних параметрах T,P існує тільки одне рішення рівняння Ван-дер-Ваальса. Така ізотерма наз. критичною, при цьому зникає різниця між газом і рідиною і цей стан речовини наз. критичним станом. Оцінити критичні параметри можна на підставі рівняння В-дер-В. Перепишемо його так: , У критичній точці , знайдемо це: , , З цих двох рівнянь знаходимо критичні параметри: , , . Щоб знайти сталі a, b для різних газів на експерименті фіксуються критичні параметри газів, бо теоретично отримати значення цих сталих з рівняння В-дер-В неможливо. Щоб перевірити правильність рівняння В-дер-В знайдемо величину . Експеримент дає такі значення: водень – 3,28; кисень – 3,42. Це розходження свідчить про те, що рівняння В-дер-В, яке виведено з припущення, що молекули – це тверді кулі, є неточним.

Зведене рівняння. Треба отримати рівняння стану незалежно від природи газу, тобто універсальне. Будь-які гази з однаковим(відповідним) відношенням , будуть описуватися ідентичними рівняннями. Параметри називають зведеними. , ,

У даному рівнянні немає констант для окремих газів. Воно називається зведеним рівнянням стану. З нього випливає, що якщо гази мають два однакові зведені параметри з трьох, то й третій параметр для них однаковий. Цей закон називається законом відповідних станів.