58. Теорема Нернста. Формулювання третього начала термодинаміки. Наслідки із третього начала термодинаміки. 3

59.Метод термодинамічних потенціалів. Внутрішня енергія як термодинамічний потенціал. Співвідношення Максвела. 4

60.Метод термодинамічних потенціалів. Вільна енергія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца. 4

61.Метод термодинамічних потенціалів. Ентальпія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца. 5

62. Метод термодинамічних потенціалів. Термодинамічний потенціал Гібса. Співвідношення Максвелла і рівняння Гібса-Гельмгольца. 5

63. Рівняння Ван-дер-Вальса. Їзотерми Ван-дер-Вальса. Взаємні перетворення пари та рідини. 6

64.Критичний стан. Критичні параметри. Методи визначення критичних параметрів. Зведене рівняння Ван-дер-Вальса. 7

65. Внутрішня енергія газу Ван – дер – Ваальса. 9

66. Ефект Джоуля-Томсона. 9

67.Зрідження газів і методи одержання низьких температур(Джоуля-Томпсона, адіабатного розширення, адіабатного розмагнічення). Машини Клода і Лінде. 11

68. Рідини, дифузія, в’язкість. 12

69.Явище поверхневого натягу 15

70. Крайові кути.Змочування.Умови рівноваги на межі трьох рідин та на межі рідини з іншим середовищем. 17

71.Кривизна поверхні і додатковий тиск . Формула Лапласа . Капілярні явища 18

72.Капілярно-гравітаційні хвилі. (Доведення) 19

73.Кристалічний та аморфний стан речовини. 21

74. Просторові кристалічні гратки. Сингонії. Гратки Браве. 23

75. Атомні площини. Індекси Міллера. 23

76 . Поверхнева енергія і зовнішня форма кристала . Закон Кюрі та Вульфа . 24

77. Класифікація кристалів за типами зв’язку в кристалічній гратці. 24

78. Дефекти кристалічної гратки. Дефекти за Шотткі і за Френкелем. Температурна залежність концентрації. 26

79.Теплоємність твердих тіл. Закони Дюлонга і Пті та Джоуля і Каппа. Недоліки класичної теорії теплоємності твердих тіл. 27

80. Квантова теорія теплоємності твердих тіл Планка-Енштейна. 27

81. Квантова теорія теплоємності твердих тіл Дебая-Борна . Температура Дебая. 27

83. Кипіння та конденсація на ядрах.. Камера Вільсона, бульбашкова камера. 28

84. Фазові переходи II роду. Співвідношення Ернста 29

85. Рідкі розчини. Закон Генрі. Закон Рауля. Наслідки з них. 29

86. Осмос. Осмотичний тиск. Закон Вант-Гоффа. Вплив дисоціації під час розчинення на осмотичний тиск. 30

58. Теорема Нернста. Формулювання третього начала термодинаміки. Наслідки із третього начала термодинаміки.

Теорема Нернста:

При прямуванні температури до абсолютного нуля, зміна ентропії прямує до деякої кінцевої межі, яка не залежить від значень параметрів, що визначають рівноважний стан системи.

- Формулювання Планка.

Дов. S=k*ln(G) – термодинамічна ймовірність (кількість мікростанів, через які можна представити даний мікростан)

(ɦw/2 – енергія нульових коливань, якою нехтують.)

Т = 0, k->G=1-> lnG =0 -> S=0.

Формулювання 1:

Абсолютний нуль недосяжний, адже тоді можна було б створити машину ККД якої рівна 100%.

, Т₂ = 0 -> = 1 -> неможливо за ІІ началом термодинаміки

Формулювання 2 :Неможливо створити вічний двигун ІІІ роду.

Н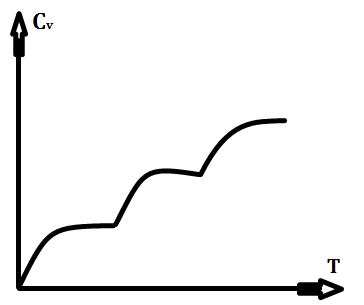 аслідки 3 начала термодинаміки:

1). При наближенні температури до 0(К), будь-яка теплоємність прямує до 0.

V = const

бQ = C_vdT

dS = бQ / T = C_vdT / T;

S – S₀ =

S = S₀ + = S =

C_v = _V = _V = _V Т -> 0, lnT -> -∞, C_v ->0.

C_p = C_v + R – для ідеальних газів

2). При наближенні температури до абсолютного нуля, ізотерма співпадає з адіабатою:

PV = const, ,

γ = (C_p / C_v) -> 1.

59.Метод термодинамічних потенціалів. Внутрішня енергія як термодинамічний потенціал. Співвідношення Максвела.

Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.

Якщо розглядати внутрішню енергію U Розглядати як потенціальну енергію, виражену через незалежні змінні S i V, то можна вважати вн. енергію термодинамічним потенціалом.

Тоді для U=U(S, V) отримуємо співвідношення Максвела

60.Метод термодинамічних потенціалів. Вільна енергія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца.

Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.

Якщо розглядати вільну енергію F як величину, виражену через незалежні змінні V i T, то можна вважати вільну енергію термодинамічним потенціалом.

Тоді для F=F(V, T) отримуємо співвідношення Максвела .

За рівнянням Гіббса-Гельмгольца вільна енергія визначається так:

.

61.Метод термодинамічних потенціалів. Ентальпія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца.

Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.

Якщо розглядати ентальпію I як величину, виражену через незалежні змінні S i P, то можна вважати вільну енергію термодинамічним потенціалом.

Тоді для U=U(S, P) отримуємо співвідношення Максвела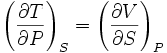

За рівнянням Гіббса-Гельмгольца ентальпія визначається так: .

62. Метод термодинамічних потенціалів. Термодинамічний потенціал Гібса. Співвідношення Максвелла і рівняння Гібса-Гельмгольца.

Якщо процес квазістатичний, то . Для такого процесу рівняння першого начала термодинаміки

Можна представити у вигляді

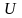Якщо ввести ентальпію , то можна виключити та отримати

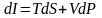
В термодинаміку було введено дві важливі функції: вільна енергія F, введена Гельмгольцем, і термодинамічний потенціал G , введений Гібсом. Ці функції виражаються співвідношенням

F=U-TS (1), G=F+PV=U-TS+PV .(2)

Їх диференціали При ізотермічному процесі dT=0, а тому dF = - PdV = - δA. Звідси A=F₁-F₂ .Отже, вільна енергія є функцією стану системи, втрати якої в квазистатичномуу процесі дають роботу, зроблену системою. Термодинамічний потенціал Гібса слід розглядати як функцію від T i P: G=G(T,P) (3). Такого роду співвідношення називається канонічним рівнянням стану речовини. Канонічне рівняння стану, містить повний обсяг інформації про термічні та калоричні властивості речовини.

­­­ (4) З цього рівняння З означення функції F i G слідує U=F+TS, I=G+TS. Підставив вираз ентропії . Це рівняння називається рівнянням Гібса-Гельмгольца. Далі вторинним диференціюванням із співвідношення (4) знаходимо Це співвідношення називається співвідношенням Максвелла. Воно використовується для виводу різних співвідношень між величинами, що характеризують термодинамічно рівноважні стани системи. Такий метод називається методом термолинамічних потенціалів.