Раскроем знак суммы относительно неизвестных a0 и a1

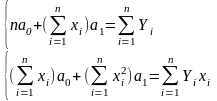
Решая эту систему линейных алгебраических уравнений, находят значения коэффициентов a₀, a_1.

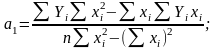
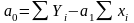
Указанный метод обобщается на случай многочлена n порядка. В этом случае

а для получения неизвестных необходимо решить систему из n алгебраических линейных уравнений (СЛАУ). Метод наименьших квадратов используют и при аппроксимации экспериментальных данных нелинейными функциями (дробно- рациональной, показательной, экспоненциальной, логарифмической и т.п.).

Например, если надо получить y= f(x) в виде y = ax^b , то преобразуя ее к выражению, lg y_i = lg a + b lg x_i и вводя новые переменные получим

z_i = с + b x_i , где z_i= lg y_i , а с = lg a

Коэффициенты c, b находятся методом наименьших квадратов. Затем определяется

a = 10^c .

Для решения СЛАУ существует много методов, но целесообразно рассмотреть один из них – метод Гаусса, который и разработал метод наименьших квадратов (МНК) в1795 году.

Законы природы записаны на языке математики

Галилео. Галилей (1564 - 1642)

§ 2.1.4 Методы и алгоритмы решения системы линейных алгебраических уравнений.

2.1.4.1 Основные понятия и обозначения.

Задачи автоматизации технологических процессов часто сводятся к системе линейных алгебраических уравнений (СЛАУ). Например, при обработке результатов эксперимента по оценке статических характеристик объектов управления. Кроме того, в методах решения дифференциальных уравнений, когда они заменяются системой разностных уравнений необходимо решать СЛАУ.

Наиболее распространенными являются две формы представления СЛАУ: координатная

a₁₁x₁+ a₁₂x₂+ + a₁nx_n = b₁



a_n1x₁+ a_n2x₂+ + a_nnx_n = b_n

и матричная.

AX=B , где

1. квадратная матрица коэффициентов при неизвестных;

X - вектор столбец неизвестных;

B - вектор столбец свободных членов.

В ряде случаев решаются системы уравнений с некоторыми специальными видами (структурами) матриц: - симметрическая (ее элементы расположены симметрично относительно главной диагонали a_{i j}=a_{j i});

3. верхняя треугольная с равными нулю элементами, расположенными ниже диагонали;

4. клеточная (её ненулевые элементы составляют отдельные группы – клетки);

5. ленточная (её ненулевые элементы составляют ленту, параллельную диагонали);

6. единичная и нулевая матрицы.

Выбор метода решения СЛАУ зависит от структуры матрицы А.

Существует два типа методов решения СЛАУ - прямые и итерационные. Прямые используют конечные соотношения (формулы) для вычисления неизвестных. Они дают решение после выполнения заранее известного числа операций. Они просты и универсальны, но не учитывают структуру матрицы А. Существенным недостатком прямых методов, является накапливание погрешностей (из-за ограниченности разрядной сетки ЭВМ) в процессе решения, поскольку на любом этапе используют результаты предыдущих операций. Это особенно опасно для больших систем, когда резко возрастает общее число операций, а также для плохо обусловленных систем, весьма чувствительных к погрешностям. Поэтому прямые методы используются обычно для систем с n меньше 200 и плотно заполненной матрицей.

Итерационные методы - это методы последовательных приближений. В них сначала задается некоторое начальное приближение, а затем по некоторому алгоритму проводиться один цикл вычислений называемый итерацией. Результатом итерации является следующее приближение. Итерации проводят до получения решения с требуемой точностью.

2.1.4.2. Прямые методы решения системы линейных алгебраических уравнений .

В литературе описано несколько видов прямых методы решения СЛАУ: матричный, Крамера, Гаусса, квадратного корня, отражения, прогонки, оптимального исключения и другие. Алгоритм матричного метода основан на следующем свойстве матриц:

Если det A 0 , то существует обратная матрица _-^-1 . Умножив правую и левую части матричного выражения СЛАУ, получим _-^-1 = _-^-1 или  = _-^-1 . Алгоритм использует операции обращения и умножения матриц.

Формулы Крамера не что иное, как частный случай матричного метода. x_n = /_n , где  и _n соответствующие определители. = det A . а _n определитель . в котором i столбец заменен столбцом свободных членов b_i .

Идея метода Гаусса состоит в том, что исходную СЛАУ с прямоугольной матрицей коэффициентов при неизвестных преобразуют к верхней треугольной. Например, если для системы третьего порядка исходное уравнение (а) преобразуют к форме (с):

a₁₁x₁+ a₁₂x₂+ a₁₃x₃ = b₁ a₁₁x₁+ a₁₂x₂+ a₁₃x₃ = b₁ a₁₁x₁+ a₁₂x₂+ a₁₃x₃ = b₁

a₂₁x₁+ a₂₂x₂+ a₂₃x₃ = b₂ a^ ₂₂ x₂+ a^ ₂₃x₃ = b^ ₂ a^ ₂₂ x₂+ a^ ₂₃x₃ = b^₂

a₃₁x₁+ a₃₂x₂+ a₃₃x₃ = b₃ a^ ₃₂ x₂ +a^ ₃₃ x₃ = b^ ₃ a^ ₃₃ x₃ = b^ ₃

(а) (b) (с)

Коэффициенты a^ ₂₂ , a^ _{23 ,} b^ ₂ , b^ 3, a^ ₃₃ , b^₂ , b^ ₃ вычисляются по следующему алгоритму.

1. Коэффициенты первого уравнения -1(а) разделить на a₁₁ затем умножить на a₂₁ и вычесть из него второе - 2(а). Аналогичную операцию проделать с уравнениями 1(а) и 3(а). В результате сформируется система (b).

2. Коэффициенты второго уравнения 2(b) разделить на a^ ₂₂ затем умножить на a^ ₃₂ и вычесть из него третье 3(b). В результате сформируется система (с).

Эта процедура называется прямым ходом алгоритма. Обратным ходом называют вычисление корней из системы (с). Одной из модификаций метода Гаусса является алгоритм с выбором главного элемента. Требование неравенства нулю диагональных элементов a_kk , на которые происходит деление в процессе исключения переменных. заменяется более жестким: из всех оставшихся элементов в k-ом столбце элементов нужно выбрать наибольший по модулю и переставить уравнения так , чтобы этот элемент оказался на месте элемента a_kk .

Пример 1 Задана СЛАУ. Решить методом Гаусса.

Прямой ход

2.7x₁+ 3.3x₂+ 1.3x₃ = 2.1 2.7x₁+ 3.3x₂+ 1.3x₃ = 2.1 2.7x₁+ 3.3x₂+ 1.3x₃ = 2.1

3.5x₁- 1.7x₂+ 2.8x₃ = 1.7 5.98x₂ -1.11x₃ = 1.02 5.98x₂ - 1.11x₃ = 1.02

4.1x₁+ 5.8x₂- 1.7x₃ = 0.8 - 0.79 x₂ +3.67 x₃ = 2.39 -3.52x₃ = -2. 52

Исходная система. Первое прямое преобразование. Второе прямое преобразование

a^ ₂₂ = (3.3/2.7)·3.5 – (-1.7) =5.98; a^ ₂₃ = (1.3/2.7)·3.5 – (2.8)= - 1.11; b^ ₂ =(2.1/2.7)·3.5 – (1.7)= 1.02

a^ ₃₂ = (3.3/2.7)·4.1 – (5.8) = - 0.79 a^ ₃₃ =(1.3/2.7)·4.1 – (-1.7)= 3.67 b^ ₃ =(2.1/2.7)·4.1 – (0.8)= 2.39

a^ ₃₃ = (- 1.11/5.98)·( - 0.79 ) - 3.67 = -3.52 b^ ₃ = (1.02/5.98)·( - 0.79) - 2.39 = -2. 52

После второго прямого преобразования исходная система приведена к треугольной.

Обратный ход. x₃ = -2. 52/(-3.52) = 0.7159 x₂ = (1.02 – (-1.11·0.7159 ))/5.98 = 0.3035

x₁ = (2.1 – 1.3·0.7159 – 3.3· 0.7159)/2.7 = 0.0621

Проверка 2.7·0.0.061+ 3.3·0.3035+ 1.3·0.7159 = 2.0999. Невязка 2.1 – 2.0999 = 0.0001.

3.5·0.061- 1.7·0.3035+ 2.8·0.7159 = 1.7021 Невязка 1.7 – 1.7021 = - 0.021. Допустимо.

2.1.4.2. Итерационные методы решения системы линейных алгебраических уравнений.

Суть итерационных методов сводится к следующему.

1.Исходная система AX=b приводится к виду CX= BX+ D, где матрицы C,B и вектор D определяются по матрице А и вектору b .

2.Расставляются индексы по номерам приближений с заданием нулевого приближения CX^(k+1)= BX^k+ D , k = 0,1,2,... где x⁽⁰⁾ - заданный вектор x⁽⁰⁾ =(x₁⁽⁰⁾ , x₂⁽⁰⁾ ,..., x_n⁽⁰⁾).

3.Итерационный процесс останавливают, когда норма вектора ||x^k - x^(k-1) || < 

Различные итерационные методы отличаются первыми двумя шагами. Метод простой итерации предполагает, что C = E=1 , тогда X = BX + D при условии сходимости метода ||B|| < 1.

В координатной записи это выглядит так

x₁^(k+1) = b₁₁ x₁^(k) + b₁₂ x₂^(k) +.....+ b_1n x_n^(k) + d₁

x₂^(k+1) = b₂₁ x₁^(k) + b₂₂ x₂^(k) +.....+ b_2n x_n^(k) + d₂

_{.......................................................................................................}

x_n^(k+1) = b_n1 x₁^(k) + b_n2 x₂^(k) +.....+ bn_1n x_n^(k) + d_n,

где 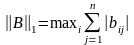первая норма матрицы B. Суммируют абсолютные значения коэффициентов при неизвестных по строкам и выбирают максимальное значение. Можно использовать также вторую и третью нормы.

,

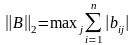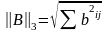
Метод Гаусса - Зейделя отличается от метода простой итерации лишь тем, что при вычислении (k+ 1) приближения, полученные x^(k+1) компоненты вектора x^(k+1) сразу же используются в вычислениях.

x₁^(k+1) = b₁₁ x₁^(k) + b₁₂ x₂^(k) +.....+ b_1n x_n^(k) + d₁

x₂^(k+1) = b₂₁ x₁^(k+1) + b₂₂ x₂^(k) +.....+ b_2n x_n^(k) + d₂

_{.......................................................................................................}

x_n^(k+1) = b_n1 x₁^(k+1) + b_n2 x₂^(k) +.....+ bn_1n x_n^(k) + d_n

Начальный вектор X⁽⁰⁾ задается k = 0, 1, 2 ... В матричной записи это можно представить так:

X^(k+1) = Ux^(k) +Lx^(k+1) + d , где матрицы U, L получены разложением В в сумму В = U + L

U - верхняя треугольная часть матрицы В, включая диагональ;

L - нижняя под диагональная матрицы B т.е. в методе Гаусса - Зейделя C = ( E - L ), B = U .

Условие сходимости итерационного процесса ||( E - L )^-1 B|| < 1

Пример 2 Задана СЛАУ. Решить методом простой итерации.

4x₁+ 0.24x₂ – 0.08x₃ = 8 x₁ = 2 – 0.06x₂ + 0.02x₃

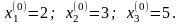
0.09x₁ + 3x₂ – 0.15x₃ = 9 x₂ = 3 – 0.03x₁ + 0.05x₃

0.04x₁ – 0.08x₂ + 4x₃ = 20 x₃ = 5 – 0.01x₁ + 0.02x_{2 Нулевое приближение (свободные члены)}

_{Исходная система Преобразованная система || B || = {0.08, 0.08, 0.03} Условие сходимости соблюдается.}

_{Условие сходимости – диагональные коэффициенты должны быть больше суммы остальных в матрице исходной СЛАУ.}

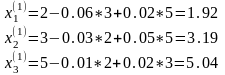Первое приближение

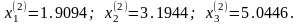Второе приближение

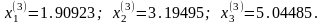Третье приближение

Итерации можно прекратить, так как разница между вторым и третьим приближением мала.

Тестовые задания для проверки усвоения темы.

1. y_i = (x-x₀)/(x₁-x₀)×( y₁ – y₀) + y_{0 .} Это выражение для интерполяционного многочлена Лагранжа?

2. x₀ = 2 y₀ =7.2 , x₁ = 3 , y₁ = 5.6 . Найти коэффициенты линейного уравнения P_n(x) = a₀ + a₁x..

3. Для условий задания 2 построить интерполяционный многочлен Лагранжа и вычислить значение функции при x = 2.7.

x₀ = 1 y₀ =1.4 , x₁ = 1.5 , y₁ = 2.6 , x₂ = 2 y₂ =9.2 , x₃ = 2.5 , y₃ = 15.6 . Найти коэффициенты нелинейного уравнения y = ax^b .

4. a₁₁x₁+ a₁₂x₂+ + a₁nx_n = b₁



a_n1x₁+ a_n2x₂+ + a_nnx_n = b_n

Это матричная форма записи СЛАУ?

5. Чем отличается итерационный метод решения СЛАУ, от прямого?

6. Решить заданную СЛАУ методом Гаусса.

7. Решить заданную СЛАУ методом простой итерации.

8. Проверить условие сходимости заданной исходной СЛАУ.

9. Проверить условие сходимости преобразованной СЛАУ.