Лекция№1

Введение.

Сигнал – это любой физический процесс, который содержит и переносит информацию.

Особый интерес представляют такие типы сигналов:

- речь (или речевой сигнал),

- звуковые и музыкальные сигналы,

- видеоизображения,

- сигнал радио- и гидролокаторов (радаров и сонаров),

- сигналы, излучаемые живыми объектами (биосигналы),

- сигналы, излучаемые техническими объектами,

- сигналы, регистрируемые различными датчиками.

Хотя природа сложна по своей сути, сложнее, чем мы думали ранее, большинство естественных сигналов являются аналоговыми. Это означает, что физические величины, описывающие сигнал изменяются во времени непрерывно (звуковые давления, интенсивность электромагнитных волн и т.п.).

При цифровой обработке сигналов аналоговый сигнал подвергается двум операциям:

- дискретизации по времени (в соответствии с теоремой Котельникова-Шеннона-Найквиста),

- квантованию по уровню.

В результате этих двух операций сигнал преобразуется в последовательность цифровых значений (отсчетов), которые далее и обрабатываются.

Любая задача обработки сигналов в технических системах сводиться к преобразованию множества Х входных сигналов ( ) в множество Y выходных сигналов ( ). Правило G, по которому осуществляется это преобразование

,

называется оператором или алгоритмом обработки сигналов. Физический объект, реализующий это правило, называется системой обработки сигналов (примеры, компьютер с соответствующим программным обеспечением, сотовый телефон и т.п.).

Цифровая обработка сигналов имеет ряд преимуществ по сравнению с аналоговой. Эти преимущества столь велики, что мы, по сути дела, живем в «цифровом мире» («digital world»). Эти преимущества разбиваются на три группы.

1. Принципиальные преимущества ЦОС.

- большая гибкость (или многофункциональность): систему ЦОС (или процессор) можно использовать для выполнения различных функций без изменения аппаратной части; это осуществляется просто путем изменения программы, это главное преимущество ЦОС;

- мультиплексирование, т.е. возможность обработки сигналов от многих источников, если это позволяет производительность процессора;

- возможность реализации практически любых преобразований, в том числе и таких, которые просто невозможны при аналоговой обработке сигналов; снимаються любые ограничения на обработку, свойственные аналоговой технике; обеспечивается реализация любых формально описываемых преобразований.

2. Реализационные преимущества ЦОС.

- гарантированная точность результата обработки, точность определяется только разрядностью процессора;

- высокая и даже абсолютная воспроизводимость результата обработки;

- полная повторяемость характеристик системы обработки от экземпляра к экземпляру;

- стабильность характеристик систем ЦОС во времени и при любой температуре;

3. Технико-эксплуатационные преимущества ЦОС.

- высокая надежность;

- малая масса и габариты систем ЦОС, отсутствие элементов L и C;

- малое энергопотребление;

- возможности диагностики систем ЦОС.

Однако системам цифровой обработки сигналов присущи и свои недостатки. Среди них:

- противоречие между скоростью обработки и затратами, для высокочастотных сигналов, требуются высокоскоростные АЦП, которые весьма дороги, сигналы с частотой 100 МГц и выше обрабатываются аналоговыми методами;

- проблемы конечной разрядности процессора, во многих практических приложениях нельзя сильно увеличивать разрядную сетку, это в свою очередь приводит к шумам квантования и специфическим эффектам конечной разрядности; это ухудшает качество системы ЦОС;

- зависимость скорости обработки от требуемой точности;

- системы ЦОС чувствительны к проникающей радиации, особенно это относиться к интегральным схемам n-МОП технологи (это ограничивает применение систем ЦОС в ядерной энергетике, в космосе и т.п.).

Основне области применения ЦОС.

1. Коммуникационные применения.

- мобильная (в частности, сотовая) связь,

- спутниковая связь,

- мультимедийная связь в компьютерных сетях, в т.ч. Інтернет,

- цифрове автоответчики, факсы, модемы,

- цифровая телефония,

- цифровое телевидение, фото и видео,

- передача даннях.

2. Обработка изображений.

- машинное зрение,

- спутниковый и космический мониторинг,

- распознавание зрительных образов.

3. Речь/аудио.

- распознавание речи,

- синтез речи,

- цифровые аудиосистемы,

- защита информации.

4. Биомедицина.

- томографы (сканеры),

- анализ электрокардиограмм, энцефалограмм и т.п.,

- улучшение качества и хранение рентгеновских снимков.

5. Военные и навигационные цели.

- безопасная связь,

- радиолокация,

- гидролокация,

- управление оружием,

- наблюдение за полем боя.

Ключевые операции ЦОС.

Несмотря на бесконечные возможности ЦОС, все системы цифровой обработки построены на небольшом числе операций, из которых строятся алгоритмы любой сложности. Эти операции называются базовыми или ключевыми. Для выполнения их требуется только четыре арифметических действия: умножение, сложение, вычитание и сдвиг. Ключевых операций всего 5:

- свертка,

- корреляция,

- фильтрация,

- дискретные частотные преобразования,

- модуляция.

Свертка.

Свертка (англ. convolution) – одна из наиболее популярных операций в ЦОС. Например, через свертку осуществляется фильтрация. Для двух конечных цифровых последовательностей x(n) и h(n) длиной N, и N₂ соответственно свертка определяется как

, n =0, 1, …, (M-1),

где * - символ свертки,

M = N₁ + N₂ – 1.

h(k) – обычно рассматривается как импульсная характеристика системы.

Корреляция.

Существует две формы корреляции: взаимная корреляция и автокорреляция.

Взаимная корреляционная функция (ВКФ) – это мера линейного сходства двух сигналов.

ВКФ определяется как

n = 0, 1, 2, …

где x(k), y(k) – коррелируемые последовательности длиной n.

Автокорреляционная функция (АКФ) – подразумевает существование только одного сигнала и дает информацию о его поведении во времени.

Цифровая фильтрация.

Цифровая фильтрация – это операция

где h(k), k = 0, 1, …, N – коэффициенты фильтра, а x(k) и y(k) - соответственно входной и выходной сигналы фильтра.

По сути, фильтрация – это свертка входного сигнала с импульсной характеристикой фильтра h(k).

Дискретные преобразования.

Дискретные преобразования позволяют переходить от временного представления сигналов к частотному, т.е. осуществляют спектральные преобразования.

Существует много дискретных преобразований, из которых самыми распространенными являются дискретное преобразование Фурье (ДПФ, dft – англ.). Оно определяется таким образом:

где W = exp(-2π/N).

Например, с помощью ДПФ можно перейти от импульсной характеристики фильтра к частотной.

Модуляция.

Цифровые сигналы редко передаются на большие расстояния. Для того, чтобы передать сигнал на расстояние нужно в соответствии со свойствами передаваемого сигнала изменить параметры некоторого высокочастотного колебания, которое называется несущим колебанием или просто несущей (carrier).

Сущность ЦОС состоит в том, что физический сигнал (напряжение, ток и т.д.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве, которое называется цифровым процессором.

Сигналы, являющиеся непрерывной функцией времени, называются аналоговыми (analog). Последовательность чисел, представляющая сигнал по ЦОС называется дискретным рядом (discrete series). Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала (samples). Обычно они берутся через равные промежутки времени Т, называемые периодом дискретизации (или интервалом дискретизации – sample time). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency) f_g = 1T.

Соответствующая ей круговая частота

ω_g = 2π/Т.

Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией (sampling), а результат преобразования - дискретным сигналом.

Частота Найквиста.

Гармонический сигнал может быть адекватно представлен дискретными отсчетами, если это частота не превышает половины частоты дискретизации. Эта частота называется частотой Найквиста f_N = f_g/2 = 1/(2T).

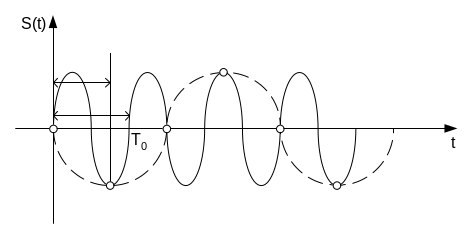
Если частота гармонического сигнала больше частоты Найквиста, восстановленный по дискретным отсчетам аналоговый сигнал (штриховая линия) также будет гармоническим, но с иной частотой (на рисунке частота сигнала f₀ = 1/T₀, период дискретизации Т = 3Т₀/4, частота дискретизации f_g = 4/3T₀, частота Найквиста f_N = f_g/2 = 2/3T₀, т.е. f₀>f_N). Такой эффект называется появлением ложных частот или алайзинтом (aliasing).

Эффекты, связанные с дискретизацией периодических процессов наглядно проявляются при кино- и видеосъемке вращающихся объектов (например, колеса автомобилей). Из-за недостаточно высокой частоты дискретизации (частоты смены кадров) быстро вращающееся колесо может выглядеть медленно вращающимся (причем в любую сторону).

Спектр дискретного сигнала.

Если дискретный сигнал представлен последовательностью отсчетов {x(k)}, то его можно записать в виде

где δ(х) – дельта-функция.

Если взять от последнего выражения преобразование Фурье, то надо учесть, что:

- спектр дельта-функции равен единице,

- задержка сигнала на х₀ во времени, приводит к умножению сигнала на комплексную экспоненту.

Тогда спектр дискретного сигнала

Отсюда видно главное свойство спектра любого дискретного сигнала: спектр является периодическим и его период равен 2π в данном случае (он определяется круговой частотой дискретизации, составляя сигнал из дельта-функций, мы выбрали Т = 1, т.е. ω_g = 2π):

Обратим внимание на размерность спектральной функции дискретного сигнала: она совпадает с размерностью отсчетов. Почему так получилось? Потому что дельта-функции времени имеют размерность частоты.

Рассмотрим другую задачу. Пусть значение x(k) являются отсчетами аналогового сигнала s(t), взятыми с периодом Т:

x(k) = s(kT).

Выясним, как в этом случае спектр дискретного сигнала связан со спектром аналогового сигнала s(ω). Дискретизованный сигнал есть последовательность δ-функций, взвешенная значениями отсчетов s(kT) аналогового сигнала s(t):

Т.к. δ(t-kT) равна нулю всюду, кроме момента t = kT, можно заменить константы s(kT) на исходный непрерывный сигнал s(t):

Сумма в последним выражении нам знакома – это периодический сигнал, он может быть представлен рябом Фурье. Коэффициенты ряда

Здесь мы учли, что интервал интегрирования равен (-Т/2, Т/2), и в него попадает только одна δ-функция, соответствующая k=0.

Т.о. периодическая последовательность δ-функций представима комплексным рядом Фурье:

где ω_n = 2πn/T.

Подставим последнее выражение в выражение для S_g и получим:

Умножение сигнала на е^jω_n^t соответствует сдвигу на ω_n, поэтому спектр дискретизированного сигнала

Т.о. спектр дискретизированного сигнала представляет собой бесконечный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t). Расстояние по частоте между соседними копиями спектра равно частоте дискретизации ω_g = 2π/Т.

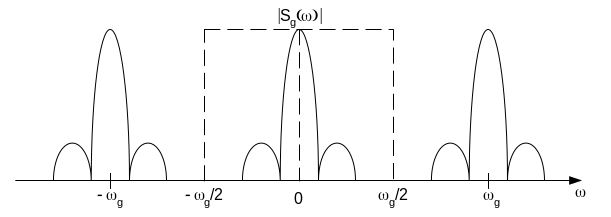
Размерность – опять размерность сигнала (из-за 1/Т).

Этот пример демонстрирует частотно-временную дуальность преобразования Фурье:

- периодический сигнал → дискретный спектр,

- периодический спектр → дискретный сигнал.

Рисунок демонстрирует способ восстановления непрерывного сигнала по дискретным отсчетам. Для этого необходимо его пропустить через ФНЧ с частотой среза, равной частоте дискретизации. АЧХ такого фильтра показана пунктиром.

Совершенно очевидно, что точное восстановление сигнала возможно, если сдвинутые копии спектра не перекрываются. Из последнего рисунка видно, что для этого необходимо, чтобы ω_g > 2ω_в.

Спектральное представление дискретного сигнала позволяет объяснить появление ложных частот (алайзин).

Пусть дискретизации подвергается гармонический сигнал с частотой ω₀, большей частоты Найквиста, но меньше частоты дискретизации.

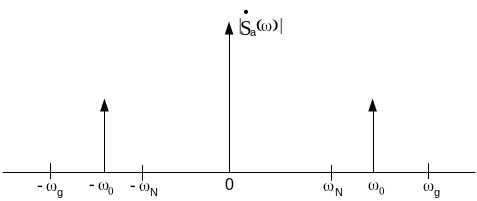
Сдвинутые копии спектра, возникающие при дискретизации, создают попадающие в полосу восстановления (от нуля до частоты Найквиста) спектральные составляющие с частотой ω_g – ω₀.

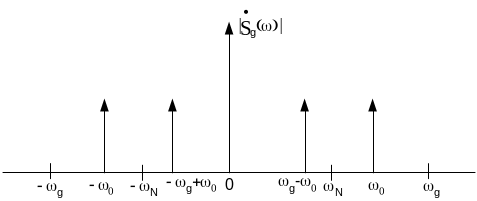
ω₀ > ω_N

Теорема Котельникова.

Теорема Котельникова (иногда в зарубежной литературе теорема Найквиста) позволяет выделить класс сигналов, для которых эти сигналы могут быть без потерь информации представлены своими дискретными отсчетами.

Мы уже видели, что если в спектре аналоговой сигнала не содержится составляющих с частотами выше частоты Найквиста, то сдвинутые копии спектров не будут прерываться. В этом случае использование идеального ФНЧ с прямоугольной АЧХ позволит выделить исходную (несдвинутую) копию спектра, сосредоточенную в окрестности нулевой частоты и, таким образом, в точности восстановить исходный аналоговый сигнал.

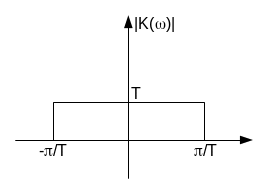
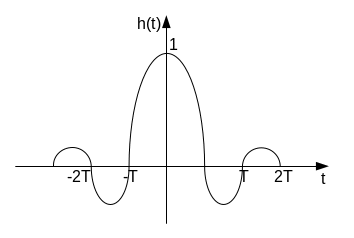
АЧХ идеального ФНЧ для восстановления показана на рисунке. Коэффициент передачи ФНЧ в полосе пропускания равен Т, а не единице, чтобы скомпенсировать множитель 4Т в формуле спектра. С помощью обратного преобразования Фурье находим импульсную характеристику фильтра

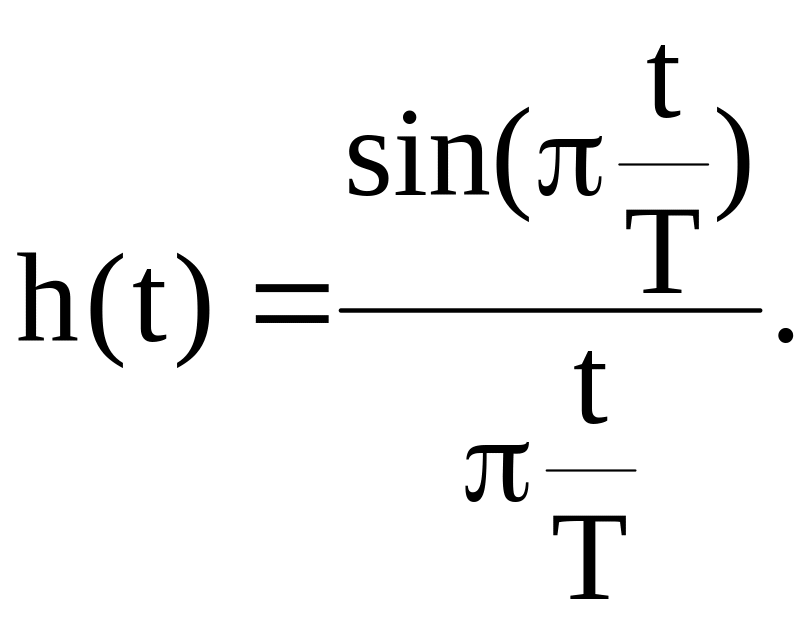
Дискретизованный сигнал – это сумма дельта-функций.

При прохождении такого сигнала через восстанавливающий фильтр НЧ каждая дельта-функция породит на выходе соответственно сдвинутую и масштабированную копию импульсной характеристики фильтра. Выходной сигнал (в точности соответствующий исходному аналоговому сигналу) будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик идеального ФНЧ

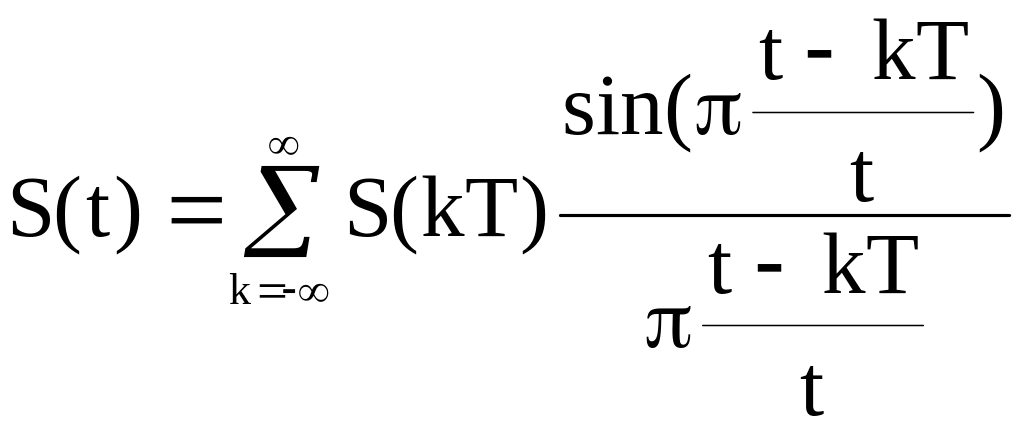
Сформулируем теорему Котельникова: любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторого значения ω_в = 2πf_в (сигнал с финитным, т.е. конечным спектром) может быть без потерь информации представлен своими отсчетами {s(kT)}, взятыми с интервалом Т, удовлетворяющим следующему равенству

В зарубежной литературе эта теорема называется теоремой Найквиста (Nyquist Theorem) или теоремой дискретизации, теоремой о выборке (sampling theorem).

Последняя формула представляет собой разложение сигнала s(t) в ряд по системе функций {φ_k(t)}, называемой базис Котельникова

Заметим, что функции всегда называются sinc-функциями.

Лекция №3

Z-преобразование.

Удобным способом представления цифровых последовательностей является Z-преобразование (Z-transform). Смысл его заключается в том, что последовательности чисел становится в соответствие функция комплексной переменной Z, которая определяется таким образом:

.

Р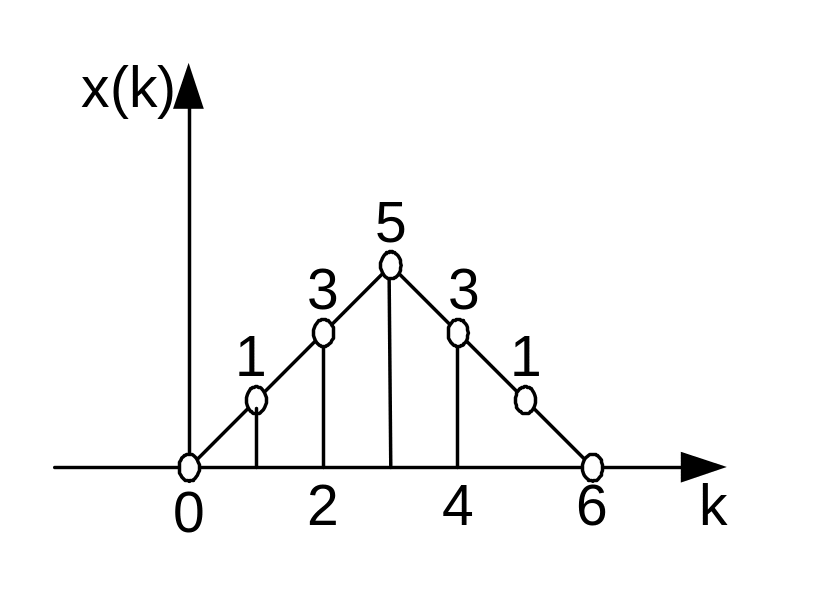 азумеется функция X(z) определена только для тех значений z, при которых записанный ряд сходится. Область, в которой Z-преобразование сходится, называется областью сходимости.

Определим Z-преобразование для последовательности, изображенной на рисунке.

, , , , , , .

.

Ряд расходится, т.е. x(k) = ∞ при z = 0. Следовательно, область сходимости – вся плоскость z, кроме точки z = 0.

Z-преобразование играет в ЦОС ту же роль, которую играет преобразование Лапласа для аналоговых сигналов. Определяющим при этом является тот факт, что Z-преобразование импульсной характеристики дискретной системы является дробно-рациональной функцией.

Обратное Z-преобразование позволяет восстановить дискретную последовательность по ее Z-образу:

.

Формально обратное Z-преобразование записывается так:

.

Интеграл берется по произвольному замкнутому контуру, расположенному в области сходимости X(z) и охватывающему все её полюсы.

На практике X(z) часто выражается в виде дробно-рациональной функции от Z^–1:

.

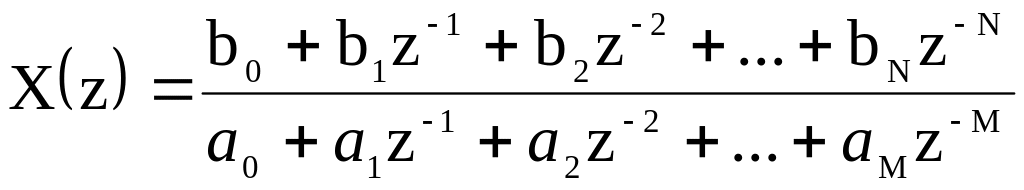Проще всего найти обратное Z-преобразование методом степенных рядов. Если дано Z-преобразование X(z) последовательности , его можно разложить в бесконечный ряд относительно Z^–1 (или Z) путём деления в столбик (его иногда называют синтетическим делением):

Пример.

1 + 2z –1 + z –2 1 – z –1 + 0,3561z –2	1 – z –1 + 0,3561z –2
	1 + 3z –1 + 3,6439z –2 + 2,5756z –3 +…
3z –1 + 0,6439z –2
3z –1 – 3z –2 + 1,0683z –3
3,6439z –2 – 1,0683z –3 3,6439z –2 – 3,6439z –3 + 1,2975z –4
2,5756z –3 – 1,2975z –4

Теперь обратное Z-преобразование:

; ; ; ;…

Связь Z-преобразования с преобразованиями Лапласа и Фурье.

Z-преобразование просто связано с преобразованиями Лапласа и Фурье.

Рассмотрим последовательность, определённую при k ≥ 0 и поставим ей в соответствие временной сигнал в виде набора дельта-функции:

,

где Т – интервал дискретизации.

Преобразование Лапласа от этого сигнала:

.

Воспользуемся фильтрующим свойством функции Дирака.

(Сначала напомним её определение – это бесконечно узкий импульс с бесконечной амплитудой, расположенный при нулевом значении аргумента:

,

нормировка ).

Фильтрующее свойство: если дельта-функция присутствует в подынтегральном выражении в виде множителя, то результат интегрирования равен значению остального подынтегрального выражения в точке, где сосредоточена δ-функция:

.

Тогда

.

Если выполнить подстановку , то преобразование Лапласа переходит в Z-преобразование.

Т.о. взаимное соответствие между Z-преобразованием X(z) и преобразованием Лапласа S(s) имеет вид:

,

.

Подобными выражениями описывается и связь Z-преобразования с преобразованием Фурье :

,

.

Рассмотрим связь S-плоскости и Z-плоскости. Пусть S-переменная Лапласа:

,

.

, ,

где ω_g – частота дискретизации.

Поскольку ω пробегает значения от – ∞ до ∞, S-плоскость отображается в Z-плоскость так.

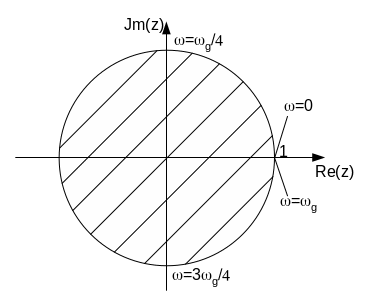
Вся ось jω отображается в единичную окружность. Левая половина S-плоскости отображается внутрь круга единичного радиуса, правая сторона Z-плоскости – во внешнюю сторону круга единичного радиуса.

Частоты и (n = 1,2,3,…) отображаются в одну и ту же точку.

Свойства Z-преобразования.

1. Линейность.

Если последовательности и имеют Z-образы X₁(z) и X₂(z), то Z-образ их линейной комбинации будет

.

2. Задержка или смещение.

Если Z-образ последовательности есть X(z), то Z-образ последовательности с задержкой на m тактов будет

.

Множитель называется оператором задержки на m тактов дискретной последовательности.

3. Свёртка.

Свёртка двух бесконечных дискретных последовательностей и :

.

.

Свёртка дискретных последовательностей соответствует произведению их Z-образов.

Обычно выход системы y(n) есть свёртка входной последовательности с её импульсной передаточной характеристикой :

.

В силу Z-свойства свёртки

.

,

называется передаточной функцией системы (trauster function).

Разностные уравнения.

Разностное уравнение описывает реальные действия, которые система ЦОС должна произвести над сигналами во временной области, чтобы получить необходимый выход.

Разностное уравнение записывается в виде

,

где х(n) – элемент входной последовательности, y(n) – элемент выходной последовательности, y(n – k) – предыдущий выход (n тактов назад), a_k, b_k – коэффициенты передаточной функции системы.

Воспользовавшись свойством задержки Z-преобразования разностные уравнения легко получить из передаточных функций и наоборот:

,

.

Разностное уравнение можно записать так

Если все коэффициенты b_i равны нулю, то выход системы y(k) зависит от элементов входной последовательности и не зависит от предыдущего выхода. Такие системы называют системы с конечной импульсной характеристикой (КИХ-системы) или нерекурсивные. В противном случае системы ЦОС называются системами с БИХ характеристиками или рекурсивными.

Способы описания дискретных систем.

1. Импульсная характеристика.

Дискретным аналогом дельта-функции является единичная импульсная функция:

Её Z-преобразование:

.

Область сходимости – вся Z-плоскость.

Выходная реакция системы на единичный импульс x₀(k) называется импульсной характеристикой дискретной системы и обозначается h(k).

Произвольный сигнал можно представить в виде линейной комбинации единичных отсчётов:

.

Выходной сигнал – это сумма импульсных характеристик.

.

Последнее выражение называется дискретной свёрткой. Для физически реализуемой системы h(k) = 0, k < 0, поэтому m ≤ k:

.

Это означает, что система при вычислении очередного отсчёта может оперировать только прошлыми значениями входного сигнала и ничего не знает о будущем.

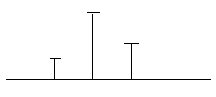
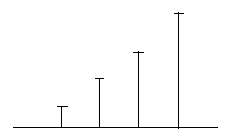
Пример вычисления дискретной свёртки.

Исходные сигналы:

1

3

2

x(k):

1

2

3

4

h(k):

Процедура вычисления:

			1	3	2
4	3	2	1

k=0:

h(0 – m): → y(0) = 1∙1 = 1;

		1	3	2
4	3	2	1

k=1:

h(1 – m): → y(1) = 1∙2 + 3∙1 = 5;

	1	3	2
4	3	2	1

k=2:

h(2 – m): → y(2) = 1∙3 + 3∙2 + 2∙1 =11;

1	3	2
4	3	2	1

k=3:

h(4 – m): → y(3) = 1∙4 + 3∙3 + 2∙2 = 17;

1	3	2
	4	3	2	1

k=4:

h(4 – m): → y(4) = 3∙4 + 2∙3 =18;

1	3	2
		4	3	2	1

k=5:

h(5 – m): → y(5) = 2∙4 =8.

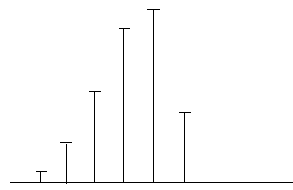
1

5

11

17

18

8

Результат y(k):

Число отсчётов линейной свёртки: M + N – 1 = 3 + 4 – 1 = 6.

Функция передачи.

.

Применение Z-преобразования и обоим частям разностного уравнения даёт:

Отсюда:

.

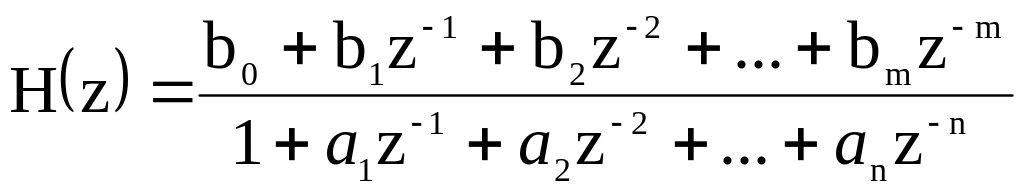Т.о. функция передачи представления отношением полиномов по отрицательным степеням переменной Z.

Частотная характеристика.

Чтобы получить выражена частотной характеристики, воспользуемся связью Z-преобразования и преобразования Фурье:

.

Видно, что частотная характеристика дискретной системы, так же, как и спектры дискретизованных сигналов есть периодическая функция частоты с периодом, равным частоте дискретизации:

.

Лекция №4.

Дискретное преобразование Фурье.

Напомним теорему Фурье.

Любой периодический сигнал f(t) можно представить в виде суммы бесконечного числа синусоидальных и косинусоидальных членов и одного постоянного слагаемого. Это представление называется рядом Фурье:

,

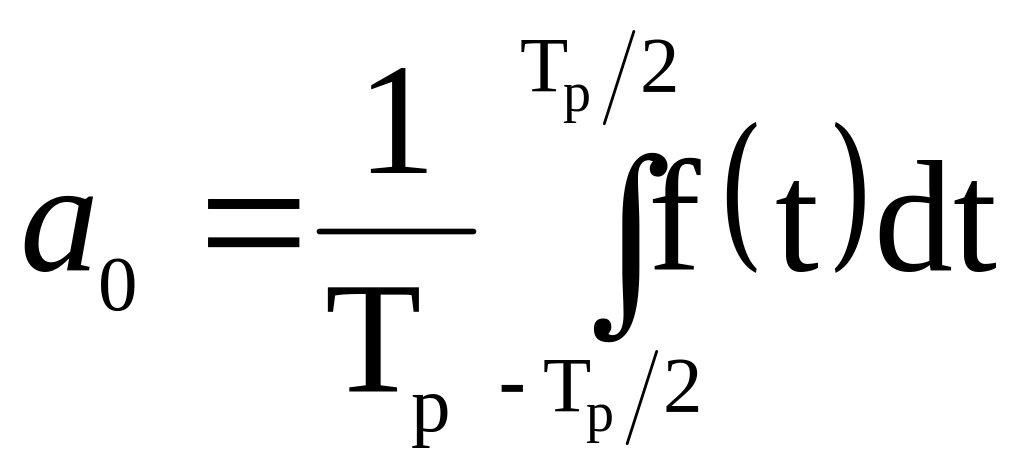- постоянная, равная сигналу f(t), усредненному по времени за период Т_р, которая имеет смысл постоянной составляющей,

, .

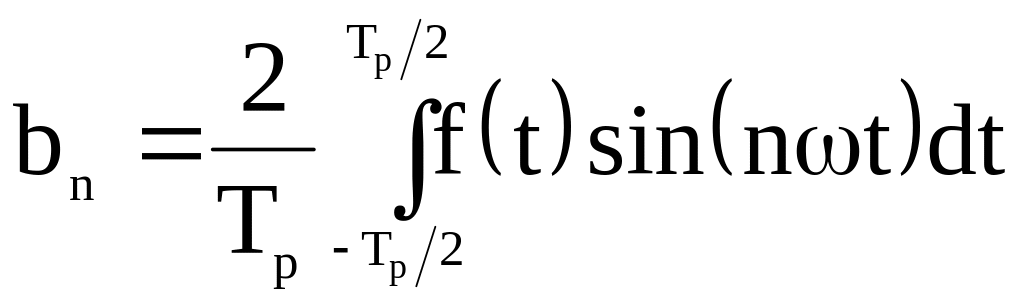Частоты то называются n-мы гармониками частоты ω. Ряд можно записать компактные с помощью формулы Эйлера

, где .

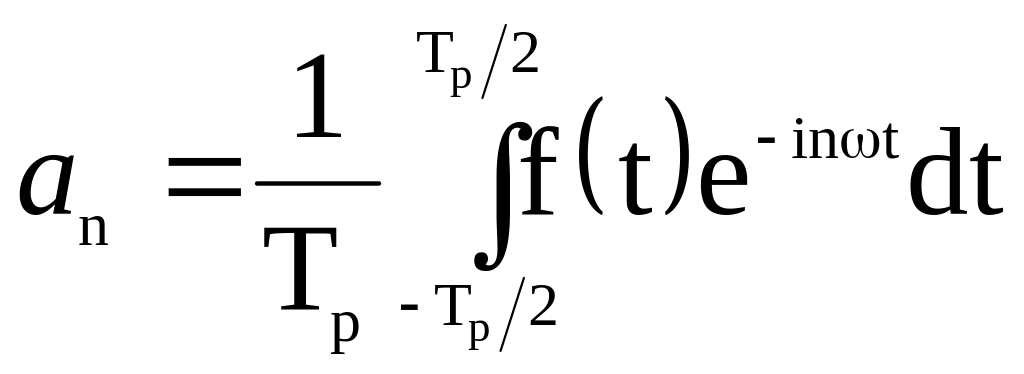Обратим внимание, что при суммировании учитываются и отрицательные частоты, физического смысла не имеющие, вследствие этого модули комплексных амплитуд численно уменьшается в два раза. Связь между комплексным и действительным представлением:

, .

Каждая гармоника характеризуется амплитудой и фазой.

Мы уже проанализировали свойства спектра дискретного сигнала. Рассмотрим теперь спектр дискретного периодического сигнала.

Пусть последовательность отсчётов является периодической с периодом N:

x(k + N) = x(k) для любого k.

Такая последовательность полностью описывается конечным набором чисел, в качестве которого можно видеть фрагмент произвольный, но длиной N, например, . Этой последовательности соответствует сигнал:

.

Он, разумеется тоже периодический, с периодом NT. Т.к. сигнал дискретный, то спектр его должен быть периодическим с периодом 2π/Т. Итак, периодический дискретный сигнал имеет периодический дискретный спектр, который также описывается набором из N чисел, т.к. один период спектра содержит гармоник.

Так как сигнал периодический, разложим его в ряд Фурье. Коэффициенты этого ряда:

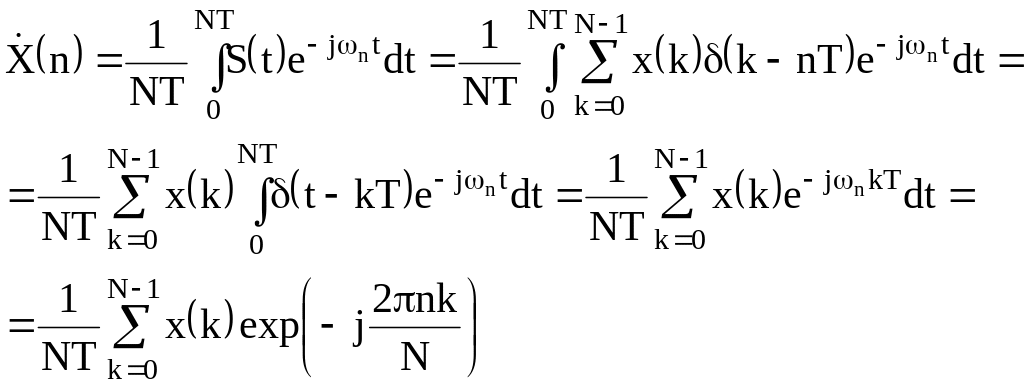
Таким образом отсчёты комплексных амплитуд гармоник представляют собой линейную комбинацию отсчётов сигнала.

Реальный масштаб времени фигурирует только в множителе 1/Т перед оператором суммирования. Т.к. мы оперируем с номерами отсчётов и гармоник спектра, множитель 1/Т обычно удаляют, подразумевая частоту дискретизации равной единице. Иногда удаляют и 1/N (единства в этом вопросе нет). Полученное выражение называется дискретным преобразованием Фурье (ДПФ; англ. Discrete Fourier Transform - DFT).

.

Обратное преобразование называется ОДПФ:

.

Пример. Пусть . N = 4.

; .

; .

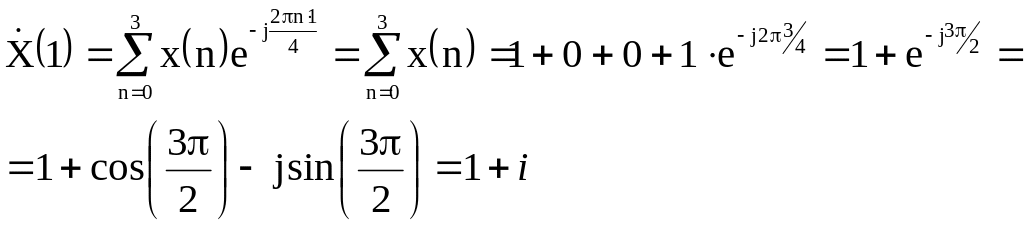
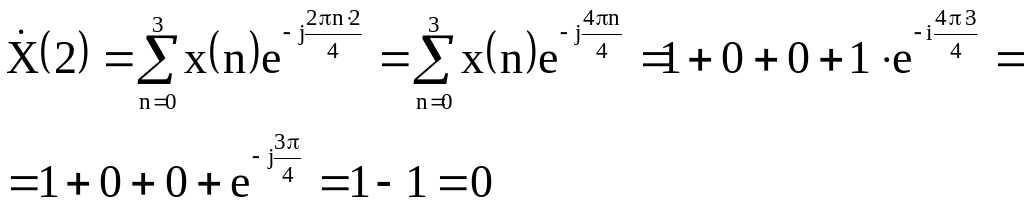
Как это выглядит графически?

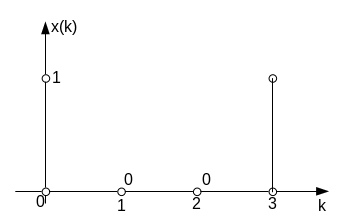
Общий вывод: амплитудный спектр ДПФ симметричен относительно отсчёта (гармоники) с номером N/2 (в нашем случае N = 2), при условии, что график содержит нулевую и (N + 1) гармоники. Фаза ДПФ антисимметрична относительно отсчёта N/2.

Если на протяжении t секунд берутся 2f_max элементов выборки сигнала в секунду, то всего отсчётов будет , так что - это частота первой гармоники. Следовательно, симметрия гармоник N/2 будет повторяться на частоте (N/2). . Значит все компоненты сигнала полностью описываются амплитудным спектром, построенным до f_max или гармоники N/2 и дальше график строить не нужно. В этом смысле частоту f_max называют частотой перегиба.

Т.е. из N действительных отсчётов сигнала получается N/2 комплексных значений ДПФ.

Свойства дискретного преобразования Фурье.

1. Симметрия.

Или в комплексном виде

, где ^* - знак комплексного сопряжения.

Гармоника с нулевым номером (постоянная составляющая) это сумма отсчётов последовательности за один период:

.

Если N чётно, то амплитуда гармоники с номером N/2 является суммой отсчётов с чередующимися знаками:

.

Спектр является сопряжено-симметричным относительно N/2. Он содержит столько же информации, сколько сам сигнал. Если исходная последовательность не является действительной, то свойство симметрии не выполняется и N комплексным отсчётам во временной области соответствует N отсчётов в частотной области, тоже комплексных.

2. Линейность.

Если последовательностями и с одним и тем же периодом соответствуют ДПФ и , то последовательности соответствует ДПФ .

3. Задержка.

Если задержать исходную последовательность на один такт , то ДПФ необходимо умножить на :

.

4. Дискретная теорема Парсеваля.

Энергия сигнала равна:

.

5. ДПФ произведения последовательностей.

Возьмём две последовательности отсчётов и одинаковой длины N и вычислим результат их поэлементного умножения:

.

Если применить к этой формуле прямое ДПФ, получим:

.

Это выражение представляет собой круговую свёртку спектров и : .

При n = 0 из последней формулы имеем дискретный аналог теоремы Рэлея.

Теорема Рэлея.

.

(Из теоремы Рэлея получается теорема Парсеваля, эти две теоремы составляют энергетическую основу спектрального анализа).

Дискретный аналог теоремы Рэлея:

.

Если последовательности и совпадают, то получает свойство 4 – дискретную теорему Парсеваля.

Круговая свёртка.

Т.к. мы рассматриваем периодические последовательности, то и суммирование при вычислении свёртки таких последовательностей следует производить по одному периоду. Такая операция называется круговой свёрткой.

.

Напомним, что операция означает взятие по модулю N, т.е. вычисление остатка от деления на N.

Круговая свёртка периодических временных последовательностей соответствует перемножению их ДПФ:

.

Круговую свёртку не путать с линейной свёрткой.

Восстановление непрерывного сигнала с помощью ДПФ.

Т.к. по сути ДПФ есть спектр дискретного периодического сигнала, ДПФ позволяет легко восстановить непрерывный периодический сигнал. Для этого в форме обратного ДПФ:

.

Необходимо заменить дискретный параметр (номер отсчёта k) на непрерывный нормированное время t/T (Т – период дискретизации):

.

Диапазон индексов суммирования смещён вниз на N/2, чтобы получить аналоговый сигнал, занимающий полосу частот от ) до π/Т.

Результат восстановления непрерывного периодического сигнала, разумеется, совпадает с результатами, получаемыми при использовании ряда Котельникова. Но использование ДПФ предпочтительнее, т.к. ряд Котельникова для периодического сигнала содержит бесконечное число слагаемых, а последнее выражение – конечное число слагаемых.

Связь ДПФ и спектра дискретного сигнала.

Имея один и тот же набор чисел (последовательность отсчётов), можно рассчитать либо спектральную функцию дискретного сигнала по формуле:

,

либо его ДПФ по формуле:

.

Естественно возникает вопрос, как связаны между собой эти две функции, полученные из одной и той же последовательности.

Сравнение двух последних выражений показывает, что ДПФ представляет собой просто дискретные отсчёты спектральной функции дискретного сигнала, соответствующие частотам :

.

По этой причине значения ДПФ иногда называют спектральными отсчётами, или спектральными бинами. Из последней формулы следует ещё один важный вывод. Если добавить к конечному набору отсчётов некоторое количество нулей, спектральная функция, естественно, не изменится, но ДПФ даст большее число спектральных отсчётов. Они будут соответствовать частотам, более тесно расположенным в интервале от нуля до частоты дискретизации.

Спектральная разрешающая способность (или разрешение)

по Рэлея.

Спектральной разрешающей способностью или разрешением по Рэлею называется минимальная разность частот двух гармонических составляющих, которые в спектре Фурье наблюдаются раздельно:

.

Бытует неправильное мнение о том, что дополнение нулями улучшает разрешение, поскольку оно увеличивает длину последовательности N. На самом же деле дополнение нулями не улучшает разрешения. Оно просто позволяет получить более детально интерполирование ДПФ.

В линейных системах действует теорема Рэлея: никакими линейными спектральными преобразованиями нельзя разделить гармонические составляющие, расположенные ближе, чем на величину 1/NT друг к другу в частотной области.

Лекция №5.

Вычислительная сложность ДПФ.

Для вычисления ДПФ необходимо выполнить некоторое количество операций умножения и сложения. Для 8-точечного ДПФ:

Замена , позволяет записать выражение:

Правая часть содержит 8 членов. Вычисление каждого из них включает операцию умножения всегда комплексной экспоненты на другой множитель, который для отсчётов сигнала действителен. Затем произведения складываются. Т.о. нам надо выполнить 8 операций комплексного умножения и 7 операций комплексного сложения. Для N-точечного ДПФ их число будет соответственно N и . Кроме того, надо вычислить 8 компонентов гармоник ( ). Для N-точечного преобразования это число равно N. Значит для 8-точечного ДПФ необходимо выполнить операции комплексного умножения и операций комплексного сложения. Для N-точечного ДПФ эти числа равны соответственно и , или примерно пар операций комплексное умножение – комплексное сложение. Если , понадобится примерно миллион пар комплексных операций. Это очень много. Надо искать какие-то пути снижения этого числа.

Понятие о быстром алгоритме.

Под быстрым алгоритмом понимают детальное описание вычислительной процедуры, которая не является очевидным способом вычисления выхода по входу и даёт экономию вычислительных операций.

Пример. Допустим надо вычислить число:

.

В записанном виде алгоритм требует 4-х умножений и 3-х сложений.

Изобразим алгоритм в виде:

.

В таком виде нам требуется всего одно умножение и два сложения.

Еще пример. Произведение двух чисел.

.

можно записать как:

, .

Здесь требуется 4 умножения и 2 сложения. Поскольку умножение более сложная операция, чем сложение, более эффективен такой алгоритм:

;

,

т.к. здесь требуется 3 умножения и 5 сложений.

Приведённые простые примеры показывают, что иногда удаётся так организовать вычислительный процесс, что мы получаем выигрыш в вычислительных операциях. Это и есть быстрый алгоритм.