57.Парадигма «Структура – поведение - результат» и ее роль в исследовании отраслевых рынков.

Разработана профессорами Гарвардской школы Мейсоном и Бэйном, первоначально ориентирована на эмпирических исследования. Высказали гипотезу о существовании связи между структурой рынка, поведением фирм и результативностью функционирования рынка. Объект исследования – возможность предсказывать параметры функционирования рынка после анализа его структуры, базовых условий и поведения фирм.

П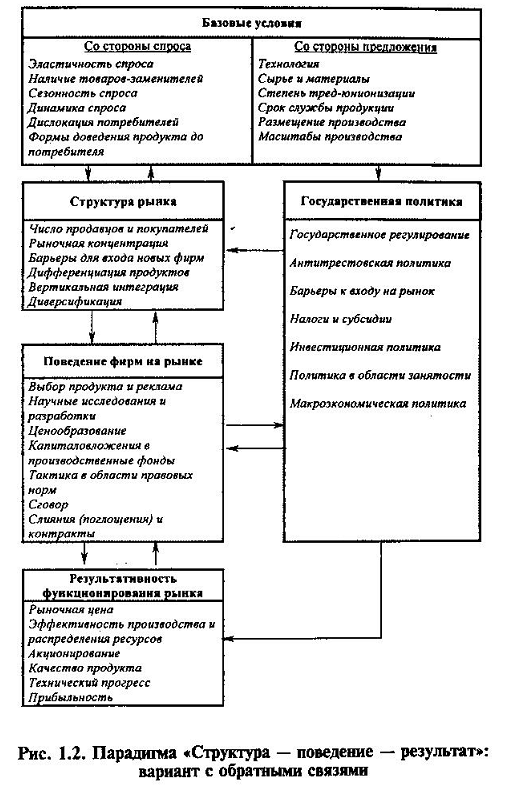 ример, показывающий наличие прямых и обратных причинно-следственных связей в рамках парадигмы Пусть небольшое количество продавцов контролирует рынок дифференцированного продукта в условиях олигополии. Дифференциация продукта оказывает влияние на поведение фирм на рынке. Они вынуждены уделять больше внимания рекламе, а также заботиться о создании новых, более совершенных, марок продукции. Такое поведение в свою очередь оказывает влияние на результативность функционирования рынка – цена устанавливается выше уровня предельных и средних издержек, норма прибыли высока. Это порождает обратные связи. Высокая рентабельность позволяет расширять рекламную кампанию и инновационную деятельность фирм. Высокий уровень издержек вызванный затратами на рекламы может затруднить вход на рынок и уменьшить потенциальное количество продавцов на рынке. Таким образом, эффективность функционирования рынка окажет влияние на поведение фирм, которое в свою очередь воздействует на структуру рынка.

Появление блока государственная политика вызвано тем, что несмотря на то, что эффективное функционирование рынка должно следовать из рациональной рыночной структуры и поведения фирм, вследствие ряда причин рынок может оказаться в кризисной ситуации. Тогда правительство может выбрать политику вмешательства и пытаться улучшить функционирование рынка, применяя политические меры, которые будут воздействовать как на структуру рынка, так и на поведение фирм.

58.Понятие антагонистической игры. Решение антагонистической игры.

В зависимости от количества игроков различают игры двух и n игроков.

По количеству стратегий игры делятся на конечные и бесконечные.

По характеру взаимодействия игры делятся на:

1)бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;

2)коалиционные (кооперативные) – могут вступать в коалиции.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

Антагонистической игрой называется игра, в которой участвуют два игрока, выигрыши которых противоположны.

Так как интересы игроков противоположны, функция F одновременно представляет выигрыш первого и проигрыш второго игрока.

Удобным способом задания игры двух участников с нулевой суммой является платежная матрица.

Каждый элемент платежной матрицы а_ij содержит числовое значение выигрыша игрока I (проигрыша игрока II), если первый применяет стратегию i, а второй — стратегию j.

При выборе первым игроком стратегии его гарантированный доход независимо от действий второго игрока составит min ai,j. Поскольку он может выбирать i самостоятельно, то целесообразно этот выбор сделать таким, чтобы он при любой стратегии противника максимизировал величину гарантированного дохода, т. е. обеспечивал получение max (min ai,j). Такой принцип выбора стратегии получил название «принцип максимина» - нижней цены игры. С другой стороны, аналогичные рассуждения могут быть проведены по поводу действий второго игрока. Его наибольший проигрыш при выборе стратегии j составит max ai,j, и, следовательно, ему следует выбирать стратегию так, чтобы минимизировать величину проигрыша при любых действиях соперника, т. е. обеспечить min (max ai,j) в этом суть принципа минимакса. – верхняя цена игры.

В случае, если верхняя и нижняя цены совпадают, то игра имеет решение в чистых стратегиях.

Теорема о неравенстве минимаксов:

max min a_ij ≤ min max a_ij

i j j i

Доказательство:

Если maxmin_ij = minmax_ij то, элемент матрицы является минимумом в своей строке и максимумом в столбце, и называется седловой точкой.

Пара чистых стратегий (i_о,j_о) игроков 1 и 2, образующая седловую точку aij , называется решением игры. При этом i_о и j_о называются оптимальными чистыми стратегиями соответственно игроков 1 и 2.