1.Адаптивные методы краткосрочного прогнозирования: метод Брауна.

Термин адаптация выступает в 3х аспектах:

Адаптация как св-во системы приспосабливаться к возможным изменениям функционирования; 2) Адаптация как сам процесс приспосабливания адаптивной системы; 3) адаптация как метод, основанный на отработке поступающей информации и приспособленный для достижения некоторого критерия оптимизации.

Под адаптацией понимается способность системы использовать получение новой информации для приближения своего поведения и структуры к оптимальным.

Если системы не адаптируются, то они перестают функционировать оптимально и перестают существовать. Адаптация не происходит мгновенно, а происходит постепенно в силу инерционности большинства систем. В процессе адаптации системы эволюционируют. Это св-во необходимо учесть в прогнозировании. Прогнозные модели должны быть адаптивными:

• Для целей краткосрочного прогнозирования это означает необходимость «уловить» последние по времени сиюминутные отклонения от сложившихся тенденций, которые вызваны кратковременным действием некоторых факторов.

• В случае среднесрочного прогнозирования нет смысла учитывать текущие кратковременные отклонения от сложившихся тенденций – они в скором времени прекратятся. Необходимо «уловить» наметившиеся в последние моменты неминуемые изменения в тенденциях развития, и, учитывая их, откорректировать прогнозную модель.

Постановка задачи:

Пусть дан временной ряд некоторого экономического показателя . Если этот ряд не имеет тенденции к росту или падению, то в случае его стационарности лучшей оценкой следующего значения будет простая средняя арифметическая, а если ряд эволюционный, то ценность текущих значений для прогноза выше, чем тех, что убывают в прошлое.

Модель Брауна:

В данной модели прогнозной оценкой на следующий шаг наблюдения выступает взвешенная средняя, причём веса наблюдения должны уменьшаться с убыванием наблюдений в прошлое:

(1.2.1)

где, - прогнозное значение параметра модели на наблюдении t+1, - фактическое значение параметра на наблюдении , – номер наблюдения с конца.

Веса заданы по экспоненциальному закону, согласно правилу:

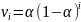(1.2.2)

где, - постоянная сглаживания.

Сумма весов в модели Брауна представляет собой ряд геометрической прогрессии, в пределе (при ) сходящийся к 1:

(1.2.3)

Подставляя (1.1.2) в (1.1.1), при выполнении (1.1.3) получим формулу:

(1.2.4)

Вынося за скобки, получим:

(1.2.5)

Обратим внимание на то, что в квадратных скобках фактически представлено прогнозное значение на наблюдение t:

(1.2.6)

Используя (1.2.6), (1.2.5) можно преобразовать следующим образом в более компактный вид:

(1.2.7)

Модель, основанная на формуле (1.2.7) названа моделью Брауна. Иногда эту модель называют «модель экспоненциального сглаживания».

Степень сглаживания определяется величиной постоянной сглаживания . Постоянная сглаживания характеризует степень адаптации модели Брауна к текущей информации. Например, если =0, то , следовательно, модель не является адаптивной; если =1, то .

Исходный ряд весов, предложенный Брауном, представляет собой бесконечную геометрическую прогрессию, о которой известно, что она сходится, если для члена геометрической прогрессии выполняется следующее условие: модуль члена геометрической прогрессии должен быть меньше единицы. Для нашего случая это условие запишется следующим образом :

(1.2.8)

Из чего, очевидно следует, что границы области применения постоянной сглаживания лежат в пределах: . Это множество значений постоянной сглаживания называют "запредельным множеством метода Брауна". В запредельном множестве постоянная сглаживания не меньше 1.

Можно выделить два случая применения модели Брауна:

1)В случае, когда необходимо сгладить имеющийся ряд данных для выявления какой-либо тенденции (обычно в случае со стационарными процессами). В этом случае обычно исследователь задаёт значение в пределах от 0 до 1.

2)В случае, когда необходимо сделать краткосрочный прогноз. В этом случае наилучший результат прогноза получается при задании в пределах от 0 до 2.

Дать трактовку запредельному множества метода Брауна (при

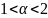) можно разложив по правилу: . В этом случае формула (1.2.7) может быть преобразована к виду:

(1.2.9)

То есть в случае, когда , модель не просто является адаптивной, так как полностью учитывает текущую информацию, но также корректируется на величину отклонения расчётного значения от фактического, то есть становится самообучающейся.

Запредельное множество метода Брауна диагностирует две возможные ситуации:

Процесс вышел за рамки простой диагностики. У него появилась некоторая тенденции в развитии.

Процесс находится на грани между эволюционной и хаотической динамикой и его математическое описание невозможно с помощью какой-либо модели. Поэтому такой процесс лучше всего прогнозировать с помощью метода Брауна работающей в запредельном множестве.