Вопрос 6. Современные концепции и теории управления прибылью: компенсационные, функциональные, монополистические, инновационные теории

Компенсационные, и функциональные, теории. Теории этой группы основаны на представлении о том, что экономическая при­быль представляет собой вознаграждение предпринимателю за его работу по коорди­нации и управлению производством. Именно предприниматель организует факторы производства в логической последовательности, планирует их эффективное сочетание и вырабатывает политику управления производством. Следовательно, прибыли явля­ются компенсацией за успешное выполнение этих функций.

Функциональные теории были предложены в начале XIX в., еще до появления круп­ных корпораций. В то время предприниматель рассматривался как высший тип труже­ника, был идентичен индивидуальному владельцу. Однако когда позже были сделаны попытки приложить функциональные теории к современ­ным государственным корпорациям с их разделением функций владения и управле­ния, результаты получились туманными и противоречивыми.

Для корпоративной формы организации бизнеса характерно делегирование вла­дельцами (держателями акций) координационной функции профессиональным адми­нистраторам, получающим заработную плату. Если вознаграждение администраторов, несмотря на контрактный характер их работы, рассматривать как прибыль, то теория по-прежнему не объясняет остаточный доход предприятия, который поступает держа­телям акций, не принимающим активного участия в управлении бизнесом.

Фрикционные и монополистические теории. Монополистические теории прибыли основаны на том, что некоторые фирмы способны занять в бизнесе монопольные позиции, которые позволяют им в течение длительного времени получать сверхпри­были. Владение патентом, авторским правом на компьютерный программный про­дукт, привилегией или очень удачным делом может дать фирме эффективную монопо­лию на достаточно длительное время. Другими факторами, которые могут создать монополию, являются масштаб производства и необходимость высоких капитальных вложений, что предохраняет действующие на данном рынке фирмы от вторжения конкурентов, а также технологические достижения, контроль над рынком или доми­нирование на нем, протекционизм и управление любым ресурсом, спрос на который превышает предложение.

Научно-технические и инновационные теории. Инновацион­ные теории основываются на том, что новая технология способствует появлению изо­бретений, а изобретения, адаптированные для бизнеса (инновациями). Многие изобретения, которые становятся инновациями нарушают равновесие системы, ранее яв­лявшейся статической.

До тех пор, пока существует конкуренция, успешная инновация может принести инновационной фирме сверхприбыль. Для одних инноваций это может длиться долго, для других - непродолжительный период.

С точки зрения бизнеса инновация может относиться к любому виду деятельности. Например, инновацией будет обнаружение новых рынков, дифференциация продук­ции (за счет чего достигается более полное удовлетворение запросов покупателей) и предложение новых изделий.

Создание новой технологии, пригодной для коммерческого использования, явля­ется результатом промышленных научно-исследовательских и опытно-конструкторских работ (НИОКР), которые могут быть выполнены как самой инновационной фирмой, так и сторонней организацией.

Инновационный процесс включает в себя две стадии: собственно изобретение, ко­торое начинается в начале НИОКР и заканчивается при разработке товара или про­цесса, и коммерциализацию, которая начинается после разработки товара или процесса и заканчивается, когда товар впервые поступает на рынок. Конечно, научно-исследова­тельские и опытно-конструкторские работы стоят дорого. Если фирма может разрабо­тать инновационные товары или процессы, пользуясь внешней технологией, то она часто может получить преимущество перед конкурентами.

МЕТОДЫ ИССЛЕДОВАНИЙ В МЕНЕДЖМЕНТЕ

Вопрос № 7 Общий вид и варианты задачи производственного планирования. Задачи построения оптимального плана в статической и динамической ситуации.

В общем случае задача производственного планирования формулируется следующим образом. Предприятие распоряжается ресурсами различных типов. Среди таких ресурсов могут быть материально-вещественные (в нашем примере – сырье), энергетические, трудовые, технические, финансовые и другие, не участвовавшие в нашем приме ре. Ресурсы каждого типа могут быть разделены на классы. Сырье – повидам сырья, трудовые – по профессиям и квалификации работников, технические – по техническим характеристикам, финансовые – по источникам финансирования и т.п. Пусть в результате такой классификации, такого разделения получилось m видов ресурсов.- Пронумеруем все виды ресурсов числами от 1 до m, буквой i будем обозначать номер вида ресурса. Таким образом, i удовлетворяет неравенству 1  i  m. Заметим, что ресурсы разных видов могут измеряться в различных единицах (тоннах, кубометрах, человеко-часах, рублях, штуках и др.). В течение планового периода предприятие обладает некоторыми доступными объемами ресурса каждого вида. Объем ресурса i-го вида, измеренный в единицах, соответствующих данному виду ресурса, обозначим посредством bi. Индекс i около буквы b указывает, что доступные объемы ресурсов разных видов могут быть различными. Из этих ресурсов предприятие способно изготавливать различную

продукцию (в нашей ситуации – Печенье и Бисквиты). Обозначим буквой n общее число видов продукции, которые может выпустить предприятие из имеющихся ресурсов. Занумеруем все виды продукции числами от 1 до n. Буквой j будем обозначать номер вида продукции, так что выполняется неравенство 1  j  n. Продукция, как и ресурсы, может измеряться в различных единицах. Пусть cj – цена, по которой предприятие реализует каждую единицу продукции j-го вида. Индекс j около буквы c указывает, что цена разных видов продукции может быть различной. Производство продукции требует затрат ресурсов. Объем затрат зависит от вида ресурса, вида продукции и количества единиц продукции. Обозначим посредством aij норму затрат ресурса i-го вида на производство продукции j-го вида. Другими словами, aij – это количество

ресурса i-го вида, затрачиваемое при производстве единицы продукции j-го вида. Задача оптимального использования ресурсов, задача производственного планирования, состоит в том, чтобы определить, какую продукцию и в каком объеме следует изготовить предприятию из имещихся ресурсов с тем, чтобы доход от реализации продукции был наибольшим.

Построим математическую модель задачи. Сначала введем переменные. Посредством xj обозначим искомый объем выпуска продукции j-го вида. Математическую модель можно теперь записать в следующей форме__

max(C1 X1+ C2 X2+…… Cn Xn ).

Экономическая задача поиска плана производства продукции, дающего наибольший доход, превращается в математическую задачу поиска максимального значения целевой функции от n переменных приусловии, что значения этих переменных подчинены системе ограничений, имеющих форму неравенств. Всякий набор значений переменных ( x1, x2 ,xn ) называется планом задачи. Те планы, которые удовлетворяют системе ограничений, называются допустимыми планами. Оптимальным планом называется тот из допустимых планов, который дает наибольшее значение целевой функции среди всех ее значений на допустимых планах.Само это наибольшее значение целевой функции, то есть значение целевой функции на оптимальном плане, называется оптимумом задачи. Решить задачу производственного планирования – значит найти оптимальный план и оптимум для ее математической модели.

Источник: http://elibrary.finec.ru/materials_files/338912468.pdf

Вопрос №8. Общая задача линейного программировании (ЛП). Матричная форма задачи ЛП. Графический метод решения задачи ЛП.

1. Линейное программирование или сокращенно ЛП (Linear Programming, LP) – это раздел более общей теории математического программирования (Mathematical Programming, MP).

Математическое программирование занимается изучением проблем принятия решений, которые могут быть математически сформулированы как задачи нахождения максимума (минимума) некоторой, вообще говоря, нелинейной функции (целевой функции)

многих переменных, при заданной системе ограничений на переменные решения.

Математически задача ЛП — задача нахождения наибольшего (наименьшего) значения линейной функции многих переменных при линейных ограничениях типа равенств (неравенств), когда на переменные задачи есть (нет) ограничений на знак.

В общем случае задача линейного программирования имеет вид:

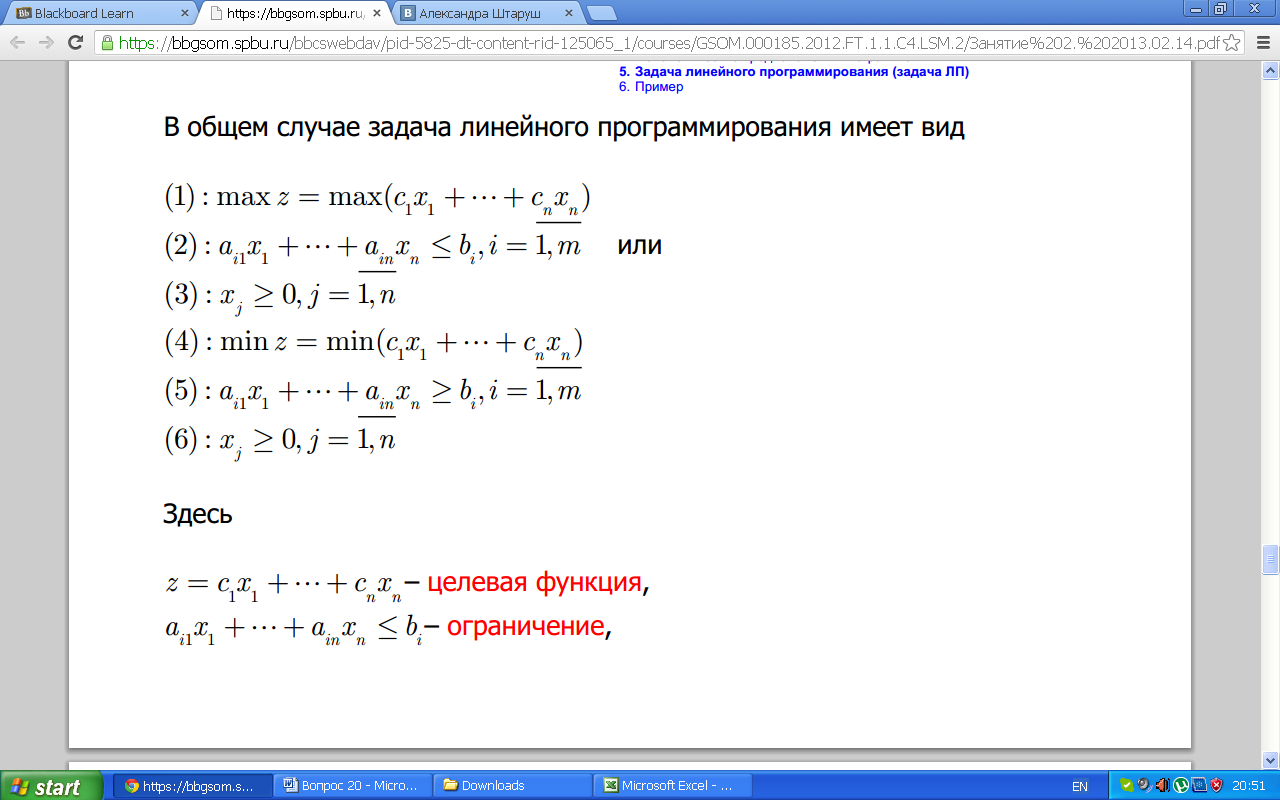
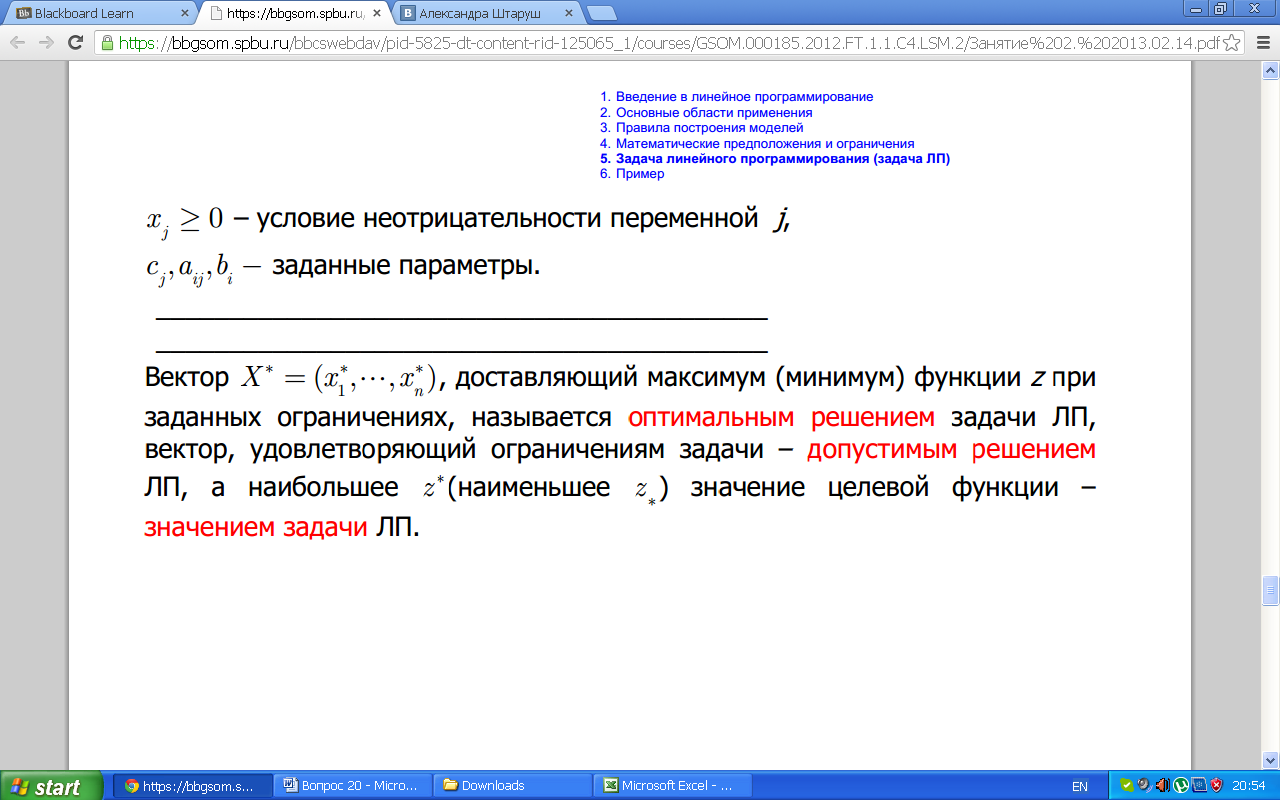
Example:

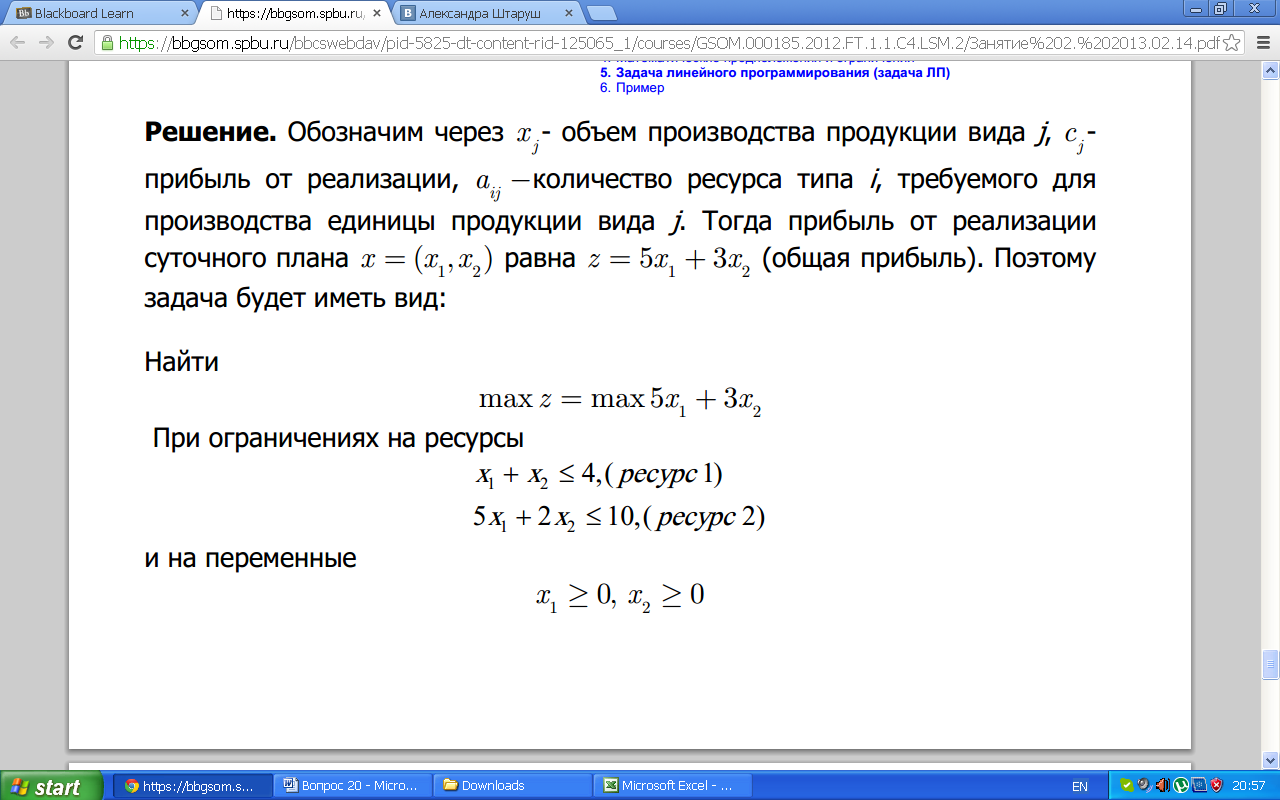
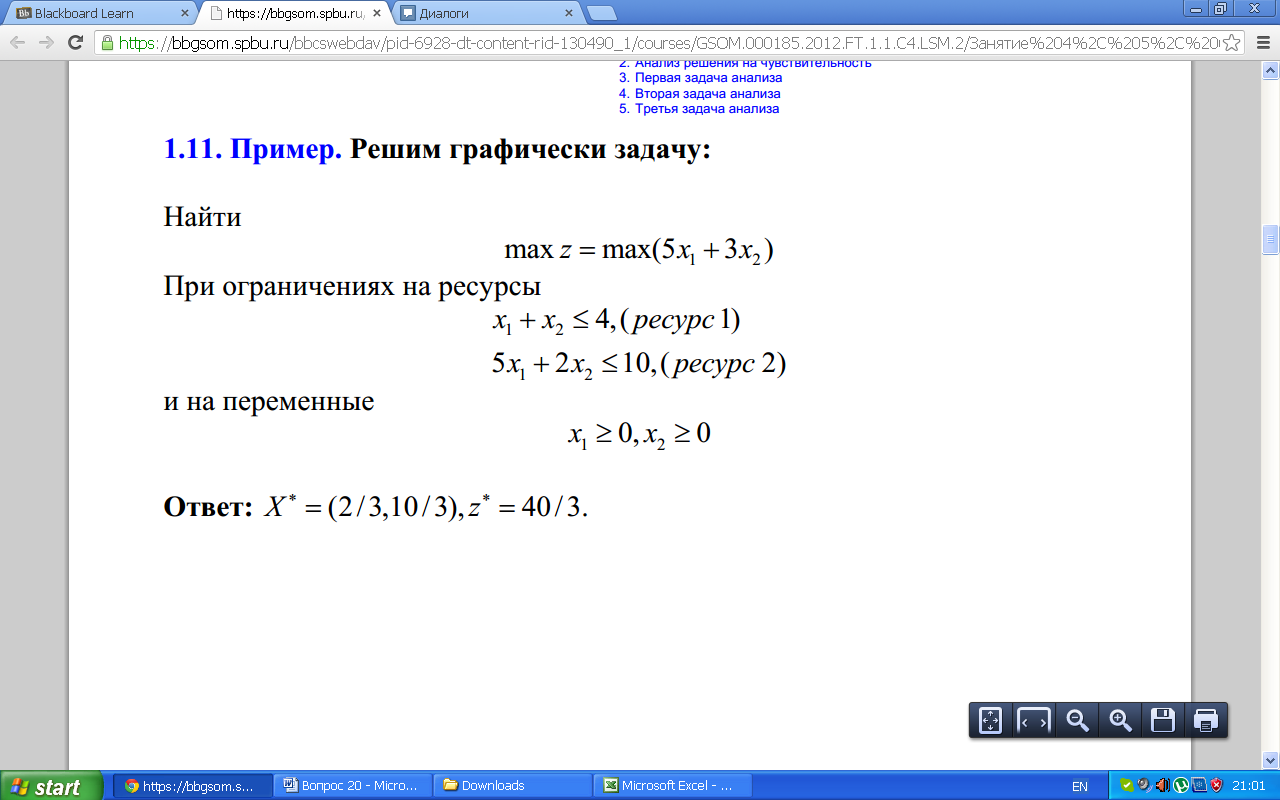
Фирма Test производит продукцию двух видов. Для производства продукции каждого вида требуются ресурсы двух типов. Для производства единицы продукции каждого вида требуется по единице ресурсов первого типа. Для производства единицы продукции первого вида требуется 5 единиц ресурса второго типа, а для производства единицы продукции второго вида — 2 единицы ресурса второго типа. Суточные запасы ресурсов равны 4 и 10 единиц соответственно. Удельная прибыль от реализации продукции составляет 5 и 3 денежные единицы соответственно. Написать математическую модель для нахождения оптимального плана производства.

2. В матричном и векторном виде эта задача может быть записана

следующим образом:

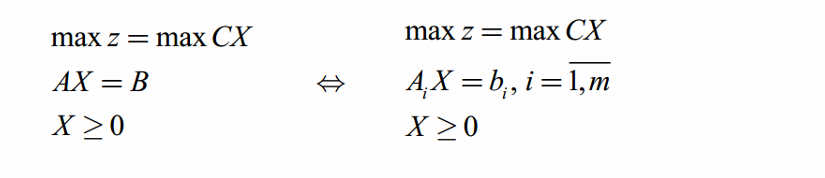
3. Графический метод применим только для задач малой размерности

(количество свободных переменных в задаче равно 2 или 3), поскольку он

основан на геометрическом построении множества допустимых решений

в задаче ЛП.

В задаче ЛП могут существовать два и более оптимальных решений

(тогда их бесконечное число) или вообще не существовать оптимального

решения.

Алгоритм графического метода:

• Записать каждое ограничение задачи ЛП как равенство (уравнение) и

нарисовать соответствующую прямую в координатной плоскости;

• Для каждого ограничения (неравенства) определить (нарисовать)

допустимую область, а затем допустимую область для всех ограничений. Оно

представляет собой пересечение таких областей для всех ограничений.

Полученная область представляет собой множество допустимых решений

задачи ЛП;

• Записать целевую функцию для произвольного уровня прибыли;

• Сдвигать линию уровня целевой функции в направлении возрастания

прибыли;

• Экстремальная (угловая) точка, которая лежит в пересечении опорной прямой

и множества допустимых решений и будет оптимальным решением;

• Определить уравнения, пересекающиеся в оптимальной крайней точке.

Решить данную систему уравнений и найти оптимальное решение.

Вычислить значение целевой функции в оптимальной точке (значение задачи

ЛП).

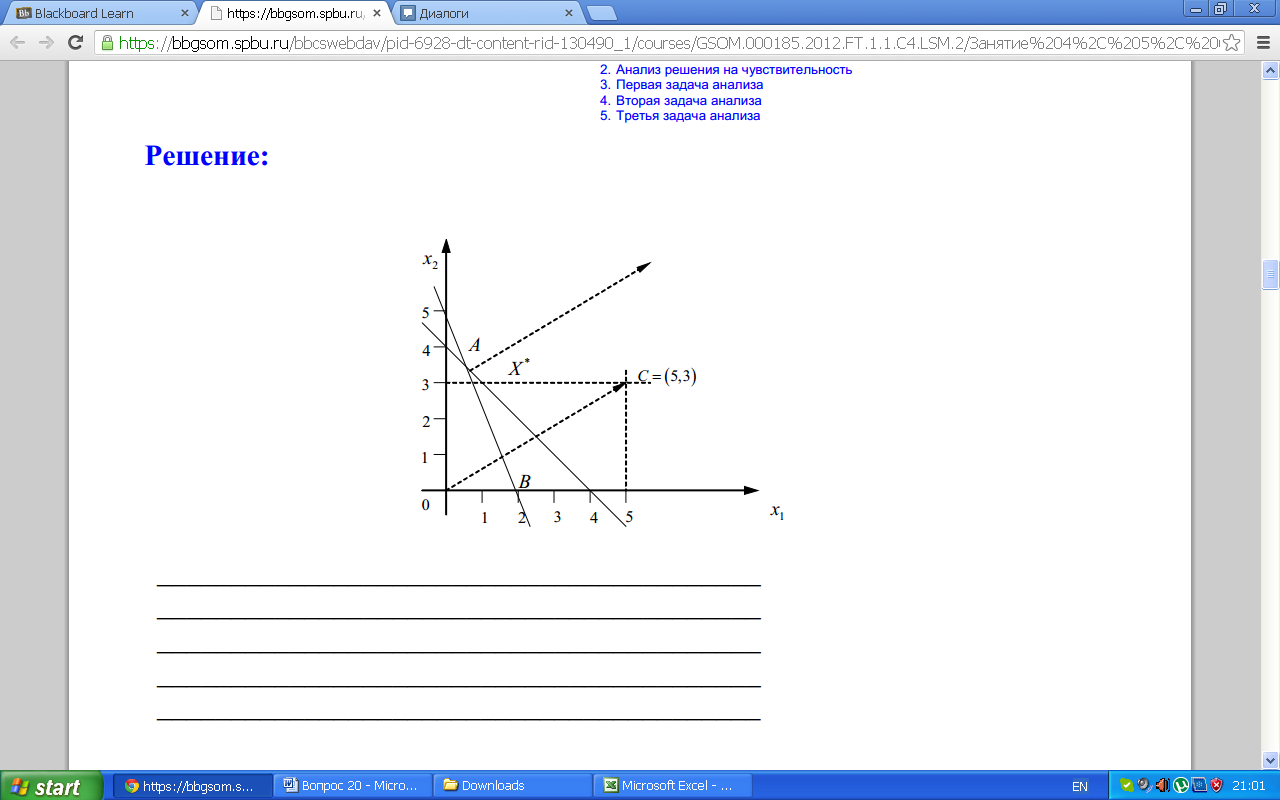
Решим графически задачу (see. Example)

10. Модель транспортной задачи линейного программирования.

Постановка задачи

        Классическая транспортная задача ЛП формулируется следующим образом.

            Имеется  m  пунктов производства (поставщиков) и n  пунктов

потребления (потребителей) однородного продукта. Заданы величины:

  - объем производства (запас) i-го поставщика,  i=1, m  ;

  - объем потребления   (спрос) j-го потребителя, i=1, n ;

   - стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к  j-му потребителю.

            Требуется составить такой план перевозок, при котором спрос

всех потребителей был бы выполнен и при этом общая стоимость всех

перевозок была бы минимальна.

            Математическая модель транспортной задачи имеет вид

                        

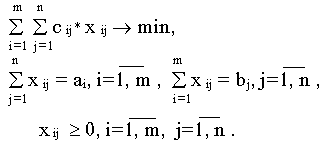
Транспортная задача, в которой суммарные запасы

                                               

и суммарные потребности

                                               

совпадают, называется закрытой моделью;  в противном случае - открытой. Открытая модель решается приведением к закрытой.

            В случае, когда суммарные запасы превышают суммарные

потребности, т.е.

                                               

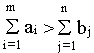
вводится фиктивный n+1 потребитель, потребности которого

                                               

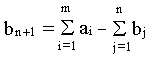
В случае, когда суммарные потребности превышают суммарные

запасы,  т.е.

                                               

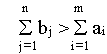
, вводится фиктивный m+1 поставщик, запасы которого

                                               

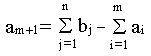
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика

полагают равными нулю, так как груз в обоих случаях не перевозится.

            Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к

закрытой модели.

Основные свойство транспортной задачи

            Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,

            1) коэффициенты  целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);

            2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);

            3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.

            В силу этих особенностей транспортная задача обладает следующими свойствами.

            Теорема 1.

Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонент.

            Доказательство.

Количество базисных компонент определяется число линейно-независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы.

            Действительно, сложив первые m ограничений и  следующие n ограничений задачи, получим

                                   

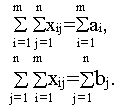
            Но в закрытой модели выполняется балансовое равенство

                                   

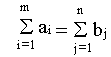
            поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно  m+n-1 и базис задачи состоит из m+n-1 компонент.

Теорема доказана

            В силу специфики содержательной постановки транспортной задачи допустимое решение называется планом, базисное допустимое решение называется опорным планом, оптимальное решение называется оптимальным планом.

            Теорема 2.

Оптимальный план закрытой модели транспортной задачи существует всегда.

            Доказательство.

Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.

            Покажем существование допустимого решения. Так как           

суммарные запасы 

                                                  

совпадают с суммарными потребностями

                                               

то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).

            Покажем ограниченность целевой функции.

            Так как

            

следовательно L ограничена снизу нулем для всех допустимых решений.

Теорема доказана

Двойственная задача

            Запишем транспортную задачу в матричном виде

            A- матрица ограничений, имеющая в соответствии с векторами х и b вид :

              

            Двойственная задача к транспортной задаче в матричном виде будет иметь вид

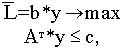
у- произвольного знака.

            Распишем двойственную задачу в скалярном виде. Обозначим компоненты вектора

                        

            Тогда

                        

и ограничения двойственной задачи будут иметь вид :

                                   

или  в общем виде двойственная задача

            

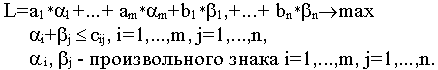
            Двойственные переменные ai, i=1,...,m, bj, j=1,...,n, называются платежами, а

                                   

- псевдостоимость перевозок единицы груза из пункта i в пункт j, i=1,...,m, j=1,...,n.