Лабораторная работа №14. Тема: интерполирование функций.
Интерполяционная формула Ньютона для равноотстоящих узлов.
Пример: Вычислить значения функции для заданных значений аргумента, используя интерполяционную формулу Ньютона для равноотстоящих узлов.
Условия задачи:
x |
y |
0,103 |
2,01284 |
0,108 |
2,03342 |
0,115 |
2,06070 |
0,120 |
2,07918 |
0,128 |
2,10721 |
0,136 |
2,13354 |
0,141 |
2,14922 |
0,150 |
2,17609 |
Вычислите значение функции у(х) при
и
.
Решение: вычисление производим по формуле
,
где
предварительно вычислим необходимые значения разделенных разностей (рисунок 14.1).
x |
y |
f |
f |
0,103 |
2,01284 |
4,1160 |
-18,23810 |
0,108 |
2,03342 |
3,8971 |
-16,76190 |
0,115 |
2,06070 |
3,6960 |
-14,78846 |
0,120 |
2,07918 |
3,5037 |
-13,28125 |
0,128 |
2,10721 |
3,2913 |
-11,94231 |
0,136 |
2,13354 |
3,1360 |
-10,74603 |
0,141 |
2,14922 |
2,9856 |
|
0,150 |
2,17609 |
|
|
Рисунок 14.1
1) Найдем значение f(0,112)
взяв за
(ближайшее меньшее). Эта строка будет
нулевой строкой, т.е.
,
f
,
f
f(0,112)= 2,03342+3,8971*(0,112-0,108)+(-16,76190)*(0,112-0,108)*(0,112-0,115)=2,04921.
2) найдем значение f(0,133)
взяв за
(ближайшее
меньшее). Эта строка будет нулевой
строкой, т.е.
,
f
f
f(0,133)=2,10721+3,2913*(0,133-0,128)+(-11,94231)*(0,133-0,128)*(0,133-0,136)=2,12385.
Ответ: f(0,112)= 2,04921.
f(0,133)= 2,12385.
Реализация в среде Excel.
Заполним исходные данные системы кК показано на рисунке 14.2.
В ячейку А11 вносим значение
,
в ячейку А12 вносим значение
.
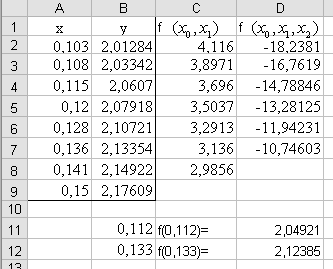
Рисунок 14.2
Вычисляем первые разделенные разности.
C2=(B3-B2)/(A3-A2) ……… Копируем эту формулу в ячейки C3,C4,C5,C6,C7,C8.
Вычисляем первые разделенные разности.
D2=(C3-C2)/(A4-A2) ……… Копируем эту формулу в ячейки D3,D4,D5,D6,D7.
Теперь непосредственно определяем значения f(x).
1)
C11=B3+C3*(A11-A3)*(A11-A4)=2,04921.
2)
C12=b6+c6*(a12-a6)+d6*(a12-a6)*(a12-a7)=2,12385.
Ответ: f(0,112)= 2,04921.
f(0,133)= 2,12385.
Задания для самоконтроля.
1)Заполните таблицу, используя следующие данные:
x |
y |
|
x |
y |
0,298 |
3,25578 |
|
0,308 |
|
0,303 |
3,17639 |
|
0,314 |
|
0,310 |
3,12180 |
|
0,325 |
|
0,317 |
3,04819 |
|
0,312 |
|
0,329 |
2,98755 |
|
0,321 |
|
0,330 |
2,91950 |
|
0,304 |
|
0,339 |
2,83598 |
|
0,299 |
|