
- •1.Абсолютті және салыстырмалы қателіктер. Нақты сандарды эем берілуі мен жуықталуы.
- •2.Матрицалар нормасы мен дәрежесі.
- •Матрицаның дәрежелері
- •Матрицаның нормасы
- •3.Сызықты алгебралық теңдеулер жүйесін шешудің тура әдістері.Гаусс әдісі
- •Гаусс әдісі. Белгісіздерді біртіндеп жою алгоритмі
- •4.Сызықты алгебралық теңдеулер жүйесін шешудің тура әдістері.Негізгі элемент әдісі
- •5.Зейдель әдісі.
- •6.Зейдель әдісінің жинақталуының жеткілікті шарттары Зейдель процесі жинақталуының жеткілікті шарттары Теорема 1. Егер
- •Нормасы бойынша Зейдель процесі жуықтау қателігінің бағасы
- •Теорема 2. Егер
- •Нормасы бойынша Зейдель процесі жуықтау қателігінің бағасы
- •Теорема 3. Егер
- •7.Минималды үйлесімсіздік әдісі мен оның қателігі Келесі сатж-ін қарастырайық
- •Минималды үйлесімсіздіктер әдісі және оның жинақтылығы
- •8.Меншікті мән және меншікті векторды итерациялық әдістерінің алгоритмдерін құру.Ньютон және Ньютон-Конторович әдістері
- •Ньютон (жанамалар) әдісі
- •Ньютон–Канторович әдісі.
- •9.Аралас әдіс. Әдістердің жинақтығы Аралас әдісі.
- •10.Гаусс,Стирлинг интерполяциялық формулалары
- •11.Лагранж интерполяциялық формулалары .Қателік бағалары
- •12.Интерпляция түйіндерін таңдаудың ең тиімді жолын таңдау
- •13.Ньютон әдісінде шешімнің бар болуы және жинақтық Ньютон (жанамалар) әдісі
- •Ең жылдам түсу әдісі және оның жинақтылығы
- •15.Симпсон және трапеция жалпы формулалары
- •16.Тордағы аппроксимация қателігі
- •17.Эйлер әдісінің модификациялары
- •Эйлер әдісін итерация әдісімен жалғастыру
- •18.Қарапайым дифференциалдық операторлардың айырымдылық аппроксимациялары. Тор және торлық функциялары. Тордағы аппроксимация қателігі
- •19.Қарапайым дифференциалдық теңдеулерге қойылған Коши есебін шешудің сандық әдістері
- •20.Эйлер әдісінің модификациялары
- •Эйлер әдісін итерация әдісімен жалғастыру
- •21.Эйлер және Рунге-Кутт әдістерін қолданып есеп шығару Эйлер әдісін итерация әдісімен жалғастыру
- •Рунге – Кутт әдісі
- •22.Көп қадамды айырымдық әдістер. Адамс әдісі Адамс схемасы
- •23.Екінші ретті теңдеулерге қойылған шекаралық есептерін шешудің айырымдылық әдістері.Қуалау әдісі
- •24.Екінші ретті теңдеулерге қойылған шекаралық есептерін шешудің айырымдылық әдістері. Орнықтылығы,қателігінің бағасы.Жинақтылығы
- •25.Ақырлы айырымдар және қуалау әдісін қолданып есеп шығару
Ең жылдам түсу әдісі және оның жинақтылығы
, матрицасы үшін (1) жүйені шешудің тиімді процесі (әдісі) қателік функциясының нөлге ұмтылуынан шығады:
 мұндағы
мұндағы
 жүйесінің дәл шешімі,
жүйесінің дәл шешімі,
 –
жуық шешімі. Әрқашан
–
жуық шешімі. Әрқашан
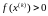 ,
,
 ,
,
 – белгісіз. Сондықтан да
– белгісіз. Сондықтан да
 ,
,

Яғни,
 функциясының кемуі
функциясының кемуі
 функционалының кемуіне эквивалентті.
функционалының кемуіне эквивалентті.
 ,
немесе
,
немесе
 ,
градиентке қарсы бағытта кемитіні
белгілі. Және де
градиентіне қарсы бағытта ең жоғарғы
жылдамдықпен кемиді.
,
градиентке қарсы бағытта кемитіні
белгілі. Және де
градиентіне қарсы бағытта ең жоғарғы
жылдамдықпен кемиді.
 шамасын есептеуге болады.
шамасын есептеуге болады.
 болатыны анық, сондықтан функционал
минимумына
болатыны анық, сондықтан функционал
минимумына
 болғанда жетеді
жүйесін шешу есебі
функционалын минимизациялау есебіне
эквивалентті.
болғанда жетеді
жүйесін шешу есебі
функционалын минимизациялау есебіне
эквивалентті.
Есеп
шешуі.
 алынып, осы
алынып, осы
 нүктесіне
нүктесіне
 функционалының
функционалының
 градиентіне қарсы бағыт есептелінеді.
Осы
нүктесінен
градиентіне қарсы бағыт есептелінеді.
Осы
нүктесінен
 минималды болатын
минималды болатын
 нүктесіне дейін таңдап алынған бағытта
қозғаламыз, яғни келесі
жуықтауы
нүктесіне дейін таңдап алынған бағытта
қозғаламыз, яғни келесі
жуықтауы
 түрінде ізделінеді, және де
түрінде ізделінеді, және де
 коэффициенті берілген
коэффициенті берілген
 бағытында,
бағытында,
 функционалының минимумы шартынан,
таңдалынады. Енді
есептейік:
функционалының минимумы шартынан,
таңдалынады. Енді
есептейік:
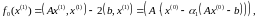
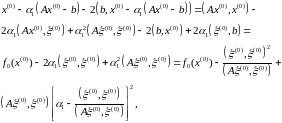
мұндағы,
 .
.
 болғандықтан,
болғандықтан,
 өрнегі өзінің минимумына
өрнегі өзінің минимумына
 нүктесінде жетеді. Және бұл минимум
нүктесінде жетеді. Және бұл минимум
 мәніне тең. Ары қарай,
мәніне тең. Ары қарай,
 өрнегін анықтаймыз және
өрнегін анықтаймыз және
 санын
санын
 өрнегінің минимум шартынан табамыз
өрнегінің минимум шартынан табамыз
 мұндағы,
мұндағы,
 ,
т. с. с. Осылардан келесі алгоритмді
аламыз:
,
т. с. с. Осылардан келесі алгоритмді
аламыз:
 ,
,


 .
Бұл жағдайда
.
Бұл жағдайда
 .
.
Теорема.
Ең жылдам түсу әдісі үшін
 бағасы орындалады. Мұндағы
бағасы орындалады. Мұндағы
 .
.
Дәлелдеуі.
Айталық
 болсын,
– бекітілген сан.
алдыңғы итерациясын пайдаланып, яғни
болсын,
– бекітілген сан.
алдыңғы итерациясын пайдаланып, яғни
 деп алып, тағы бір тиімді итерациялық
процесін жүргізейік :
деп алып, тағы бір тиімді итерациялық
процесін жүргізейік : .
Онда қателік векторлары
.
Онда қателік векторлары
 және
және
 тиімді итерациялық процесс үшін
тиімді итерациялық процесс үшін
 қатынасымен байланысады.
қатынасымен байланысады.
Айталық
 матрицасының
матрицасының
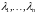 меншікті сандарына сәйкес келетін, яғни
меншікті сандарына сәйкес келетін, яғни
 ,
ортогональ және ортонормаль меншікті
векторлары болсын. Бұл жағдайда,
,
ортогональ және ортонормаль меншікті
векторлары болсын. Бұл жағдайда,
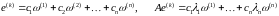 және
және
 .
Ары қарай,
.
Ары қарай,


 болғандықтан
үшін соңғы теңсіздіктен алатынымыз:
болғандықтан
үшін соңғы теңсіздіктен алатынымыз:

 ең
жылдам түсу әдісімен алынған келесі
жуықтауы болсын, онда
ең
жылдам түсу әдісімен алынған келесі
жуықтауы болсын, онда
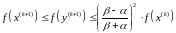 болатыны анық.
болатыны анық.
Осы
теңсіздікке индукция әдісін қолданып,
теорема тұжырымын аламыз. Шынында да
 болғандықтан,
болғандықтан,
 .
Келесі
.
Келесі
 Релей теңсіздігінде, бір рет
Релей теңсіздігінде, бір рет
 (сол жағынан), екінші рет
(сол жағынан), екінші рет
 (оң жағынан) деп пайымдап алатынымыз:
(оң жағынан) деп пайымдап алатынымыз:

немесе
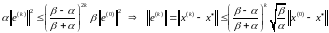 .
.
Бұл алынған өрнек – ең жылдам түсу әдісінің жинақтылық жылдамдылығының бағасы.
15.Симпсон және трапеция жалпы формулалары
Ньютон-Котесс
квадратуралық формуласында
 болған жағдайда
болған жағдайда


 – трапеция
формуласы деп аталады.
– трапеция
формуласы деп аталады.
Трапеция формуласының қалдық мүшесі

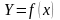 функциясы
функциясы
 аралығында екі рет дифференциалданатын,
екі рет интегралданатын функция.
аралығында екі рет дифференциалданатын,
екі рет интегралданатын функция.
 ,
,
 .
.
Егер
 ,
онда трапеция формуласының көмегімен
берілген интегралдың мәні артығымен,
ал егер
,
онда трапеция формуласының көмегімен
берілген интегралдың мәні артығымен,
ал егер
 болса, онда кемімен есептелінеді.
болса, онда кемімен есептелінеді.
Онан соң трапецияның жалпы формуласы қарастырылады.
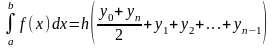

Әрі қарай Симпсон формуласы және оның қалдық мүшесі қарастырылады.
Ньютон-Котесс
квадратуралық формуласында
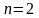 болған
жағдайда:
болған
жағдайда:


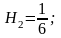
 – Симпсон
формуласы деп аталады.
– Симпсон
формуласы деп аталады.
Қалдық мүшесі:

функциясы
-да
үзіліссіз, дифферециалданатын,
 туындылары бар болсын.
туындылары бар болсын.
 нүктесін бекітіп алып, қалдық мүшені
нүктесін бекітіп алып, қалдық мүшені
 -тан
тәуелді функция.
-тан
тәуелді функция.
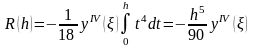 ,
,
 .
.
Онан соң Симпсонның жалпы формуласы қарастырылады.
 .
Оның қалдық мүшесі төмендегі формуламен
анықталады:
.
Оның қалдық мүшесі төмендегі формуламен
анықталады:

 деп
белгілесек, онда
деп
белгілесек, онда

