5.Зейдель әдісі.

Айталық жүйесі берілсін. Кез-келген жуықтауларын алдық дейік. Енді түбірлерінің -шы жуықтаулары белгілі деп түбірлерінің -ші жуықтауларын келесі формуласымен есептейміз

, итерация нөмірі.

Зейдель әдісі, қарапайым итерация әдісіне қарағанда, жақсы (тез) жинақтылықты береді. Бірақ-та өте көп есептеулерді қажет етеді. Қарапайым итерация әдісі жинақталмаған жағдайларда да Зейдель әдісі жинақталуы мүмкін. Зейдель әдісінің қарапайым итерация әдісінен жайырақ жинақталатын кездері де болады. Тіпті, қарапайым итерация әдісі жинақталып, Зейдель әдісі жинақталмайтын жағдайлар да болады.

6.Зейдель әдісінің жинақталуының жеткілікті шарттары Зейдель процесі жинақталуының жеткілікті шарттары Теорема 1. Егер

(1)

сызықты жүйе үшін

(2)

шарты орындалса, мұндағы онда (1) жүйені шешудің Зейдель процесі осы жүйенің жалғыз шешіміне, кез-келген бастапқы векторымен, жинақталады. (Дәлелдеусіз).

Нормасы бойынша Зейдель процесі жуықтау қателігінің бағасы

мұндағы .

Теорема 2. Егер

(1)

сызықты жүйе үшін

(3)

шарты орындалса, мұндағы онда (1) жүйені шешудің Зейдель процесі осы жүйенің жалғыз шешіміне, кез-келген бастапқы векторымен, жинақталады. (Дәлелдеусіз).

Нормасы бойынша Зейдель процесі жуықтау қателігінің бағасы

,

мұндағы ; .

Теорема 3. Егер

(1)

сызықты жүйе үшін

(4)

шарты орындалса, мұндағы онда (1) жүйені шешудің Зейдель процесі осы жүйенің жалғыз шешіміне, кез-келген бастапқы векторымен, жинақталады. (Дәлелдеусіз).

7.Минималды үйлесімсіздік әдісі мен оның қателігі Келесі сатж-ін қарастырайық

(1)

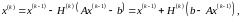
(2)

(2) теңдеуден

(3)

үшін жалғастырсақ, (3)-тен алатынымыз:

. (4)

(2) теңдіктен дәл шешімін оң және сол жақтарынан алып тастасақ, қателік векторы үшін келесі рекурентті формуласын аламыз:

. (5)

(2)-ші итерациялық процесінің жинақталуы үшін немесе , орындалуы жеткілікті.

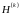матрицасының түрі қателік векторының немесе үйлесімсіздік векторының қандай да бір функционалын минимизациялау арқылы таңдалады; стационар процесте матрицасының түрі көшу матрицасының нормасын минимизациялау арқылы таңдалған.