1.Абсолютті және салыстырмалы қателіктер. Нақты сандарды эем берілуі мен жуықталуы.

Х – кезкелген бір шаманың дәл мәні, ал

х – оның жуық шамасы болсын (жуықтауы).

Х-х – жуықтаудың қателігі болып табылады. Әдетте, бұл қателіктің таңбасы елеусіз болады, сондықтан практикада оның абсолют мәні қарастырылады:

                                                                                                                                                                                                 (1)

 

е_х-х жуықтауының абсолюттік қателігі деп аталады. Көп жағдайда Х саны белгісіз болады да, (1) формуласының көмегімен х жуықтауының абсолюттік қателігін анықтауға мүмкіндік болмайды. Бірақ есептеушіге көбінесе жіберілетін қатенің абсолюттік шамасының жоғарғы шегі белгілі болады, яғни

 

                                                                                          (2)

 

теңсіздігі орынды болатын  саны белгілі болады.   жуықтауының абсолюттік қателігінің шекарасы деп аталады.

Анықтама. Сонымен х жуық санының абсолюттік қателігінің шекарасы деп осы санның е_х абсолюттік қатесінен кем емес кезкелген бір   санын айтамыз.

Мысалы, p санының жуық мән ретінде   алайық p=3,141592... сонда   жуықтауының қатесі

 

Ал оның абсолюттік қателігінің шекарасы ретінде

 санын алуға болады.

 

(2) теңсіздігі Х санының жуық шамасын артығымен және кемімен алуға мүмкіндік береді.

                                                                               (3)

 

Практикада (3) теңсіздігінің орнына

                                                                                          (4)

 

формуласын қолданады.

Абсолюттік қатесі бойынша, жүргізілген есептеулердің немесе өлшеулердің  дәлдігі туралы толық мағлұмат алуға болмайды. Жуықтау мәндерінің сапасы оның салыстырмалы қателіктері арқылы анықталады.

Анықтама. х жуықтауының салыстырмалы қателігі деп оның абсолюттік қателігінің х санына   қатынасын айтады.

Анықтама. х жуықтауының салыстырмалы қателігінің шекарасы деп абсолюттік қате шекарасының х санының модуліне қатынасын айтады, яғни

                                                                                              (5)

 

(5) формуласы қажет  болған жағдайда х санының абсолюттік қатесін, оның салыстырмалы қатесі арқылы анықтауға мүмкіндік береді.

                                                                                          (6)

2.Матрицалар нормасы мен дәрежесі.

Матрицалар теориясынан кейбір мәліметтер.

1) . 2) . 3) . 4)

Матрицаның дәрежелері

. деп келісейік. – бірлік матрица; Егер ерекше емес болса, онда . 1) . 2) .

Квадрат емес матрицаны дәрежеге шығаруға болмайды! Егер және реті бірдей матрицалар және болса, онда .

Матрицаның нормасы

, , , және типтері бірдей матрицалар , мұндағы матрицасы элементтерінің модулі. Егер және және матрицалары үшін орындалса, онда

1) , 2) , 3) . Дербес жағдайда, .

Анықтама 1. матрицасының нормасы дегеніміз төмендегі шарттарды қанағаттандыратын нақты саны:

а) , б) ( сан), ,

в) , г) .

Квадрат матрицасы үшін . в) шартын қолданып: .

Соған ұқсас: .

Анықтама 2. Норма канондық деп аталады, егер қосымша тағы екі шарт орындалса:

д) егер , онда 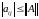, – скаляр матрицасы үшін (егер матрица бір ғана саннан тұрса), е) теңсіздігінен . Дербес жағдайда, .

үшін төмендегі нормаларын қарастырамыз:

1) 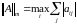, ( – норма), (I – норма), (тік жол элементтерінің қосындысы).

2. , ( – норма), (II –норма), (жатық жол элементтерінің

қосындысы).

2. ( – норма) (III –норма), (Евклид нормасы).

векторы үшін, 1) ,

2) ,

3) 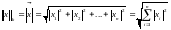– вектор модулі (ұзындығы).