3. Критерий соответствия хи-квадрат.

Количественное изучение биологических явлений обязательно требует создания гипотез, с по­мощью которых можно объяснить эти явления. Чтобы проверить ту или иную гипотезу ставят се­рию специальных опытов и полученные фактические данные сопоставляют с теоретически ожи­даемыми согласно данной гипотезе. Если есть совпадениеэто может быть достаточным ос­но­ванием для принятия гипотезы. Если же опытные данные плохо согласуются с теоретически ожи­даемыми, возникает большое сомнение в правильности предложенной гипотезы.

Степень соответствия фактических данных ожидаемым (гипотетическим) измеряется критерием со­от­ветствия хи-квадрат:

.

 фактически наблюдаемое значение признака вi-той;теоретически ожидаемое число или признак (показатель) для данной группы,kчисло групп данных.

Критерий был предложен К.Пирсоном в 1900 г. и иногда его называют критерием Пирсона.

Задача. Среди 164 детей, наследовавших от одного из родителей фактор, а от другогофактор, оказалось 46 детей с фактором, 50с фактором, 68с тем и другим,. Рассчитать ожидаемые частоты при отношении 1:2:1 между группами и определить степень соответствия эмпирических данных с помощью критерия Пирсона.

Решение:Отношение наблюдаемых частот 46:68:50, теоретически ожидаемых 41:82:41.

Зададимся уровнем значимости равным 0,05. Табличное значение критерия Пирсона для этого уровня значимости при числе степеней свободы, равном оказалось равным 5,99. Следовательно гипотезу о соответствии экспериментальных данных теоретическим можно принять, так как, .

Отметим, что при вычислении критерия хи-квадрат мы уже не ставим условия о непременной нор­маль­ности распределения. Критерий хи-квадрат может использоваться для любых распределений, ко­­то­рые мы вольны сами выбирать в своих предположениях. В этом есть некоторая уни­вер­саль­ность этого критерия.

Еще одно приложение критерия Пирсона это сравнение эмпирического распределения с нор­мальным распределением Гаусса. При этом он может быть отнесен к группе критериев про­вер­ки нормальности распределения. Единственным ограничением является тот факт, что общее число зна­чений (вариант) при пользовании этим критерием должно быть достаточно велико (не менее 40), и число значений в отдельных классах (интервалах) должно быть не менее 5. В противном случае следует объединять соседние интервалы. Число степенй свободы при проверке нор­маль­нос­ти распределения должно вычисляться как:.

4. Критерий Фишера.

Этот параметрический критерий служит для проверки нулевой гипотезы о равенстве дис­пер­сий нормально распределенных генеральных совокупностей.

Или.

При малых объемах выборок применение критерия Стьюдента может быть корректным только при условии равенства дисперсий. Поэтому прежде чем проводить проверку равенства выборочных средних значений, необходимо убедиться в правомочности использования критерия Стьюдента.

,

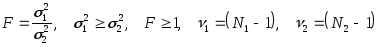где N₁, N₂  объемы выборок,₁, ₂ числа степеней свободы для этих выборок.

При пользовании таблицами следует обратить внимание, что число степеней свободы для выборки с большей по величине дисперсией выбирается как номер столбца таблицы, а для меньшей по величине дисперсии как номер строки таблицы.

Для уровня значимости по таблицам математической статистики находим табличное значение. Если, то гипотеза о равенстве дисперсий отклоняется для выбранного уровня значимости.

Пример.Изучали влияние кобальта на массу тела кроликов. Опыт проводился на двух группах животных: опытной и контрольной. Опытные получали добавку к рациону в виде водного раствора хлористого кобальта. За время опыта прибавки в весе составили в граммах:

Опыт	Контроль
580	504
692	560
700	420
621	600
640	580
561	530
630	490
680	580
	470

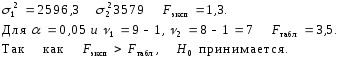
Проверка по критерию Фишера позволяет считать, что генеральные дисперсии равны.