Дислокации в упорядоченных сплавах. В сплавах с дальним порядком (сверхструктурой) атомы разного сорта закономерно чередуются в определённых кристаллографических плоскостях и направлениях.

При появлении в такой сверхструктуре обычной единичной дислокации нарушается закономерное чередование атомов, и возникает антифазная граница, обладающая повышенной энергией. Поэтому в сплавах с дальним порядком дислокации существуют парами: одна из них создаёт антифазную границу, а другая её уничтожает (рис. 5.9).

Н апример, в упорядоченных твердых растворах с ГЦК решеткой пары образуют дислокации с векторами Бюргерса a/2<110>.

Рис. 5.9. Парная дислокация в упорядоченном твердом растворе

(пунктир - антифазная граница)

Пара дислокаций, соединённая полоской антифазной границы, называется парной или сверхструктурной дислокацией. Она ведёт себя как полная единичная дислокация в сверхструктуре и её вектор Бюргерса равен единичному вектору трансляции сверхструктурной решётки.

Равновесная ширина антифазной границы обычно составляет 100 – 200 А°. Каждая из дислокаций пары может диссоциировать на дислокации Шокли, т.е. по краям антифазной границы могут находиться расщепленные дислокации с дефектами упаковки между ними.

Вопросы для самопроверки

1. Какие дислокации называют полными и какие – частичными? Ка­ковы критерии возможности протекания дислокационных реакций?

2. Как могут возникать и что собой представляют дефекты упаковки в ГЦК и ГП решетках? Что понимают под энергией дефектов упаковки?

3. Каковы векторы Бюргерса полных дислокаций, характерных для ГЦК решетки?

4. Что представляют собой частичные дислокации Шокли в ГЦК ре­шетке? Каковы их векторы Бюргерса?

5. Какие дислокации называют расщепленными? От чего зависит рав­новесная ширина расщепленных дислокаций?

6. Что представляют собой частичные дислокации Франка в ГЦК решетке? Чем они отличаются от частичных дислокаций Шокли?

7. Какой тетраэдр называют стандартным тетраэдром Томпсона? При­ведите примеры дислокационных реакций, возможных в ГЦК решетке, ис­пользуя символику стандартного тетраэдра Томпсона.

8. Какие дислокации в ГЦК решетке называют вершинными? Что представляют собой дислокации Ломер – Коттрелла?

9. Как происходит поперечное скольжение и переползание расщеплен­ных дислокаций?

10. Какие дислокации называют парными? Как движутся такие дис­локации?

Раздел 6. Пересечение дислокаций и их взаимодействие с точечными дефектами

В реальном кристалле дислокации располагаются и движутся в разных плоскостях скольжения, как параллельных, так и пересекающихся. Поэтому движущаяся дислокация встречает множество других дислокаций («лес дислокаций») и должна их пересекать.

Тема 6.1. Пересечение единичных краевых, краевой и винтовой и винтовых дислокаций

Пересечение единичных краевых дислокаций. Пусть в вертикальной плоскости движется дислокация АВ с вектором Бюргерса b₁ (рис. 6.1).

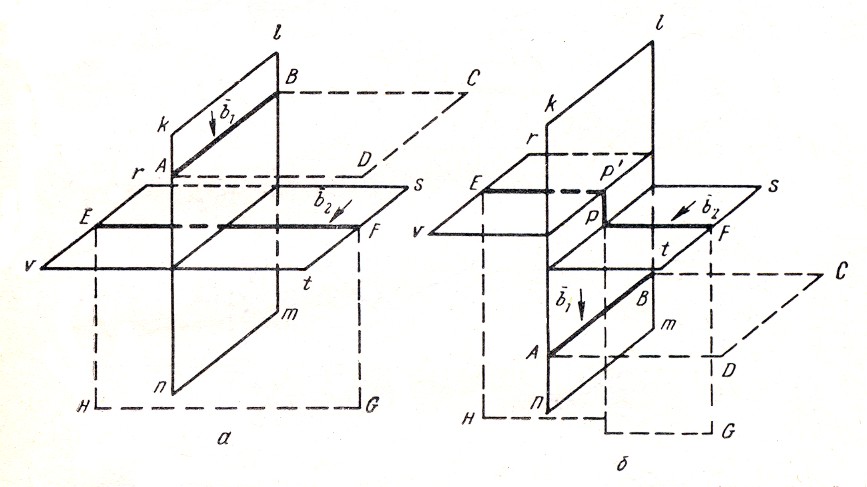
Рис. 6.1. Пересечение краевых дислокаций АВ и EF со взаимно перпендикулярными векторами Бюргерса: а) до пересечения, б) после пересечения

Линия этой дислокации является краем экстраплоскости АВСD. В горизонтальной плоскости находится неподвижная дислокация ЕF - край экстраплоскости EFGH – c вектором Бюргерса b_{2 .}

В результате движения дислокации АВ вниз правая часть кристалла сдвигается вниз относительно левой на вектор сдвига b_1. Такой сдвиг претерпевает и дислокационная линия ЕF, разбиваясь на два участка - ЕР и РF. Так как дислокация не может оборваться внутри кристалла, то эти участки должны быть соединены отрезком РР – линией дислокации с вектором Бюргерса b_2. Отрезок РР дислокационной линии является дислокационным порогом и в этом случае имеет краевую ориентацию.

На дислокации АВ порога не образуется, т.к. вектор Бюргерса b₂ дислокации ЕF параллелен линии дислокации АВ. В результате пересечения дислокация АВ становится длиннее на величину вектора Бюргерса дислокации b₂.

Рис. 6.2. Пересечение краевых дислокаций АВ и EF С параллельными векторами Бюргерса: а) до пересечения, б) после пересечения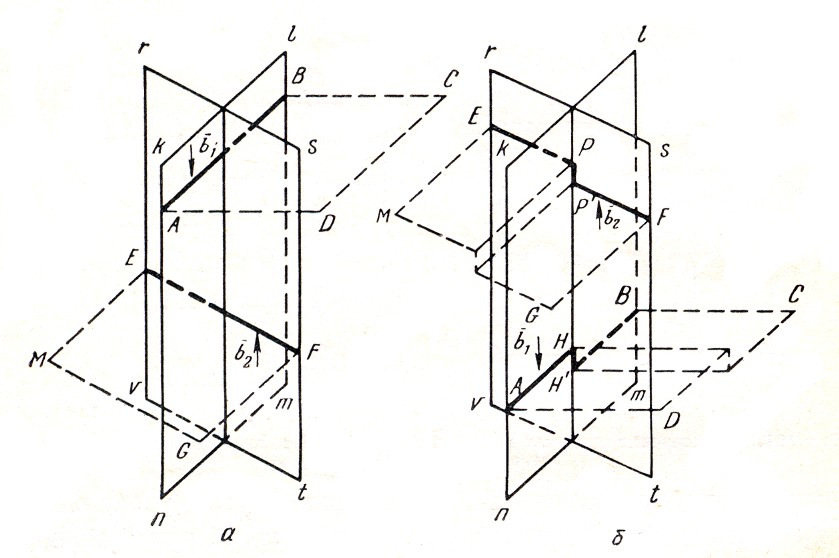

Р езультат пересечения дислокаций АВ и EF не изменится, если будет двигаться не только дислокация АВ, но и дислокация EF. Пересекающиеся дислокации могут иметь векторы Бюргерса, каждый из которых перпендикулярен линии другой дислокации (рис. 6.2).

При пробеге дислокации АВ вся правая часть кристалла смещается вниз на вектор b₁ и на дислокации EF образуется порог, равный по величине b_1. При пробеге дислокации EF снизу вверх вся передняя часть кристалла смещается вверх на вектор b₂ и на дислокации АВ образуется порог величиной b_2.

Пороги РР и НН имеет винтовую ориентацию. Они могут легко исчезнуть при скольжении дислокаций, т.к. лежат в их плоскостях скольжения. Такие неустойчивые пороги называют перегибами дислокаций.

Порог на дислокации устойчив только в том случае, если он не лежит в ее плоскости скольжения (как порог PP' на дислокации EF, рис. 6.1).

Общее правило: при пересечении двух дислокаций на каждой из них образуется порог, причём порог на одной дислокации равен по величине вектору Бюргерса другой дислокации и совпадает с ним по направлению.