Тема 5.4. Стандартный тетраэдр и дислокационные реакции в гцк-решётке

В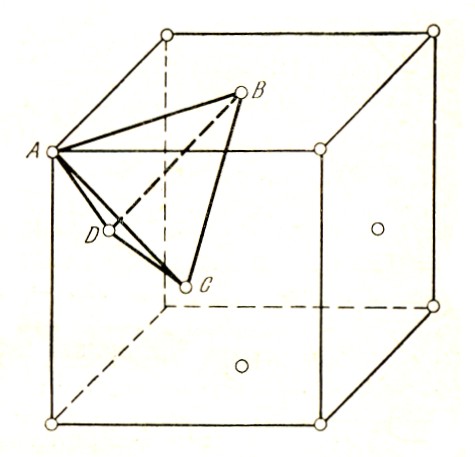 екторы Бюргерса характерных дислокаций в ГЦК решётке принято представлять, используя специальное геометрическое построение – стандартный тетраэдр Томпсона (рис. 5.6, 5.7). Его вершины совпадают с базовыми узлами ГЦК решётки, ребра расположены вдоль кристаллографических направлений <110>, а грани – четыре равносторонних треугольника – являются плоскостями {111}.

Рис. 5.6. Расположение стандартного тетраэдра Томпсона в элементарной ячейке ГЦК-решетки

Таким образом, грани тетраэдра Томпсона АВС, АBD, АСD и BCD – это все возможные плоскости скольжения{111}, а его рёбра АВ, АС, АD, ВС, ВD, СD – это все возможные векторы Бюргерса единичных полных дислокаций a/2<110> в ГЦК решетке.

Буквами α, β, γ и δ обозначены центры граней, противолежащих вершинам А, В, C и D, соответственно. Лежащие в плоскостях граней {111} отрезки Аβ, Аγ, Аδ и т.п. представляют собой все возможные векторы Бюргерса a/6<112> частичных дислокаций Шокли.

Отрезки, соединяющие вершины тетраэдра с центрами противоположных граней Аα, Вβ, Cγ и Dδ, перпендикулярны граням {111} и представляют собой все возможные векторы Бюргерса a/3<111> частичных дислокаций Франка.

С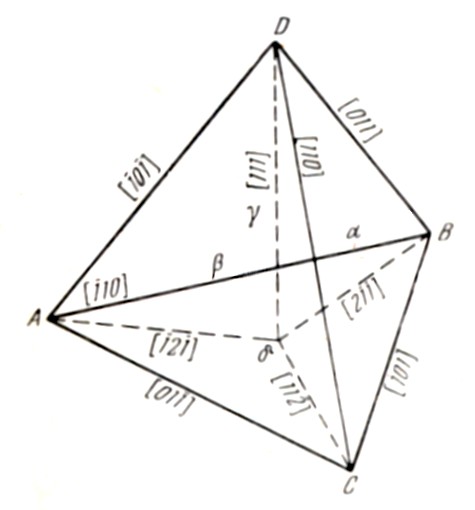 помощью стандартного тетраэдра Томпсона удобно записывать дислокационные реакции в ГЦК решётке.

Например, реакция расщепления полной единичной дислокации на две частичные дислокации Шокли может быть представлена в виде АС = Аδ + δС.

Рис. 5.7. Стандартный тетраэдр Томпсона

Эта реакция происходит в плоскости АВС. В этой же плоскости возможны подобные реакции АВ = Аδ + δВ и ВС = Вδ + δС.

Аналогичные реакции можно записать для других граней тетраэдра Томпсона. Объединение частичных дислокаций Франка и Шокли с образованием единичной полной дислокации описывает реакция Аα + αС = АС.

Критерий Франка не позволяет определить возможность протекания такой реакции

(а3/3)² >(а6/6)² +(а2/2)²

Но, учитывая, что в результате этой реакции исчезает дефект упаковки, связанный с частичной дислокацией Франка, она оказывается энергетически выгодной.

Р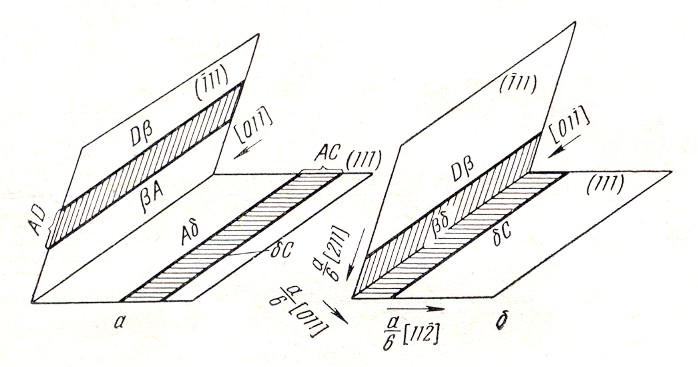 ассмотрим встречу двух расщепленных дислокаций, движущихся в пересекающихся плоскостях скольжения (рис. 5.8).

Рис. 5.8. Образование дислокации Ломер-Коттрелла

при встрече расщепленных дислокаций: а) до встречи,

б) после встречи

Пусть в плоскости АDС находится дислокация АD, расщеплённая на частичные дислокации Шокли Dβ и βA, разделённые дефектом упаковки, а в плоскости АВС находится дислокация АС, расщепленная на частичные дислокации Aδ и δC, разделенные дефектом упаковки.

При движении расщепленных дислокаций их головные частичные дислокации βА и Аδ встречаются на линии пересечения плоскостей скольжения ADC и ABC и вступают в реакцию:

βА + Аδ = βδ, образуя новую частичную дислокацию.

Отрезок βδ соединяет центры двух граней, параллелен ребру DВ и равен одной третьей отрезка DВ. Следовательно, вектор Бюргерса этой частичной дислокации равен а/6 [011].

Дислокационная реакция βА + Аδ = βδ даёт большой выигрыш энергии:

(а6/6)²+ (а6/6)² > (а2/6)² , а²/3 >а²/18

Линия дислокации а/6[011] находится в вершине двугранного угла, образованного встретившимися дефектами упаковки, и поэтому такую дислокацию называют вершинной.

Линия вершинной дислокации и её вектор Бюргерса лежат в плоскости, не являющейся плоскостью скольжения. Поэтому вершинная дислокация, связанная с двумя частичными дислокациями Шокли и клинообразным дефектом упаковки, неподвижна.

Эту совокупность из трёх частичных дислокаций и клинообразного дефекта упаковки называют дислокацией Ломер-Коттрелла. Поскольку дислокации Ломер-Коттрелла неподвижны, их называют иногда барьерами Ломер-Коттрелла.

Двойникующая дислокация. При пластической деформации и отжиге часто происходит двойникование – такая перестройка кристаллической решётки, при которой две части кристалла становятся симметричными относительно плоскости двойникования.

Граница между этими частями может не совпадать по всей длине с одной и той же кристаллографической плоскостью и может ступенчато переходить из одной кристаллографической плоскости в другую.

В металлах с ГЦК решёткой двойникующими являются дислокации с векторами Бюргерса a/6<112>, лежащие в плоскостях {111}.