- •Математические модели в сетях связи
- •Содержание
- •1. Развитие технологий и услуг связи
- •1.1 Показатели развития
- •1.2 Тенденции развития технологий и услуг
- •1.3 Развитие технологий М2М
- •2.3 Иллюстрации (надежность сетей связи)
- •2. Задачи моделирования
- •2.1 Задачи моделирования, предметная область
- •2.2 Пример моделей развития технологий и услуг
- •2.4 Задачи модели по уровням ВОС (OSI)
- •3. Сети связи
- •3.1 Состав сети связи
- •3.2 Структура сети связи
- •3.3 Узел связи
- •3.4 Линия связи
- •3.5 Пространственное разделение каналов
- •3.6 Частотное разделение каналов
- •3.7 Временное разделение каналов (формирование ИКМ)
- •3.8 Временное разделение каналов (формирование пакетов)
- •4. Математическое моделирование
- •Введение
- •4.1 Сеть связи как СМО
- •2 Сеть связи как СМО
- •2.1.4 Технические нормы на показатели функционирования сетей передачи данных Минкомсвязи
- •2.1.5 Показатели надежности (Минкомсвязи)
- •3. Модели систем массового обслуживания
- •Обозначения СМО по Кендаллу (Kendall’s notation)
- •4.2 Характеристики потоков заявок
- •4.3 Простейший поток вызовов
- •4.4 Другие виды потоков
- •4.5 Поток с простым последействием
- •4.6 Поток с ограниченным последействием
- •4.7 Поток Пальма, потоки Эрланга
- •2.4 Другие виды потоков
- •4.8 Случайный процесс, характеристики трафика как случайного процесса
- •4.9 Автокорреляционная функция
- •Пример реализаций простейшего, самоподобного и антиперсистентного потоков
- •5.2 Поток освобождений
- •Изменение нагрузки, ЧНН, концентрация нагрузки
- •Расчет нагрузки
- •7. Пропускная способность
- •9.2 Функция распределения времени ожидания
- •9.3 Среднее время ожидания
- •9.4 Формула Полячека-Хинчина
- •9.5 Частные случаи
- •10 Основные результаты
- •11 Сети СМО
- •Сети СМО
- •Сложение случайных чисел (справка)
- •Последовательность СМО
- •Пример
- •11.2 Объект измерений
- •11.3 Анализируемые параметры
- •11.4 План проведения измерений
- •11.5 Обработка результатов
- •11.5.1 Точечные оценки
- •11.5.2 Интервальные оценки
- •11.5.3 Доверительный интервал для вероятности
- •11.5.3 Гистограммы, функции распределения
- •11.5.4 Функция распределения
- •12.2 Общая структура имитационной событийной модели
- •12.4 Получение потока событий с заданными свойствами
- •Эмпирический закон распределения
- •13. Пример расчета пропускной способности
- •Порядок расчета
- •расчет необходимой пропускной способности
- •Вариант расчета для общего случая
- •Модели выбора структуры
- •14.2 Пути, маршруты, веса, длина пути
- •14.3 Некоторые определения
- •14.4 Матричные представления
- •14.5 Деревья, остов графа
- •Алгоритмы теории графов (задачи динамического программирования)
- •14.5 Структура с наименьшей протяженностью линий (задача поиска кратчайшего остова (SST) графа)
- •14.5 Пример алгоритма Краскала
- •14.5 Кратчайший остов (SST) графа (алгоритм Прима)
- •14.5 Пример алгоритма Прима
- •14.5 Пример алгоритма Прима (продолжение)
- •Размещение узла в сети связи
- •размещение центров графа
- •размещение центров графа
- •размещение медиан графа
- •размещение медиан графа
- •размещение узла в сети связи – поиск центра и медианы графа
- •Вычисление длин кратчайших путей между вершинами
- •Алгоритм Флойда-Уоршалла
- •Алгоритм Флойда-Уоршалла (нахождение всех кратчайших путей в графе)
- •Пример реализации алгоритма Флойда-Уоршелла на VB
- •Алгоритм Дейкстры (описание 2)
- •Алгоритм Дейкстры (пример)
- •Алгоритм Дейкстры (поиск кратчайшего пути)
- •Некоторые алгоритмы поиска путей
- •Приближенные решения
- •муравьиный алгоритм
- •муравьиный алгоритм
- •Задачи кластерного анализа
- •Кластерный анализ
- •Кластерный анализ
- •Алгоритм кластеризации FOREL
- •Алгоритм кластеризации k-средних
- •Пример кластеризации
- •Применение кластерного анализа для выбора структуры сети
- •3.3 Выбор координат базовой станции при произвольном законе распределения трафика по территории
- •4.4 Моделирование и реализация, публикации
- •Модели надежности сети связи
- •3.3 Модели надежности сети связи
- •Общие определения
- •Иллюстрации (надежность сетей связи)
- •3.5 Метод добавления-удаления (IE – inclusion-exclusion)
- •Имитационное моделирование (надежность)
- •Задачи прогнозирования
- •Оптимизация сети связи
- •1. Исходные данные
- •2. Свойства трафика
- •Задачи прогнозирования (примеры)
- •Задачи прогнозирования (примеры)
- •Ассоциативный метод
- •Результаты(пример)
- •Аналитические модели 1. Линейная регрессия
- •Миграция трафика
- •Миграция на примере ОТТ сервисов
- •Задачи оптимизации
- •2 Надежность сети связи
- •Аналитические методы оптимизации
- •Экстремумы функции
- •Безусловная оптимизация
- •Условная оптимизация
- •2 Выпуклые функции
- •3 Условия Каруша-Куна-Таккера (ККТ)
- •Численные методы оптимизации
- •1 Общий алгоритм численных методов
- •Покоординатный спуск (пример)
- •3.2 Метод Хука-Дживса (поиск по образцу)
- •Метод Хука-Дживса (пример)
- •3.3 Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику)
- •Симплекс метод Нелдера-Мида (пример)
- •3.4 Комплексный метод Бокса (Условная оптимизация)
- •3.5 Метод штрафных функций (Условная оптимизация)
- •3.4 Некоторые другие методы оптимизации выпуклых функций
- •4 Стохастические методы
- •4.1 Слепой случайный поиск
- •4.2 Эволюционный метод (генетический алгоритм)
- •Генетический алгоритм
- •Генетический алгоритм (пример)
- •Случайные графы (модели сети беспроводной связи)
- •Случайные графы
- •Случайные графы
- •Изменение связности сети
- •Влияние числа узлов сети на дисперсию связности
- •Приоритетное обслуживание
- •Алгоритм распределения трафика
- •Оптимизация структуры сети
- •Расписание управления трафиком
- •Качество обслуживания
- •Постановка задачи
- •Модель расписания управления трафиком
- •Задача оптимизации расписания управления
- •Модель реакции трафика
- •Условия переноса трафика
- •Описание стоимости времени
- •Пример оптимизации расписания управления
- •Балансировка трафика
- •Балансировка трафика
- •(нечеткие методы)
- •(нечеткие методы)
- •1. Распределение случайной величины
- •Случайная величина
- •Распределение случайной величины
- •Примеры функций распределения случайной величины (1)
- •Примеры функций распределения случайной величины (2)
- •Плотность распределения случайной величины
- •Примеры плотности распределения (1)
- •Примеры – равномерное распределение (2)
- •Числовые характеристики случайной величины (1)
- •Числовые характеристики случайной величины (2)
- •Числовые характеристики случайной величины (3)
- •2. Некоторые распределения вероятностей
- •3. Численные методы оптимизации Ф1П
- •ОДУ (Справка)
- •4. Модель ВОС (OSI)
- •Модель взаимодействия открытых систем (ВОС)
- •4. Параметры некоторых кодеков
- •Параметры кодеков
- •5. Курсовые проекты
- •Задание на курсовое проектирование
Модель реакции трафика
Полагаем, что провайдер услуг может |
|
|||
Часть рисунка с идентификатором отношения rId5 не найдена в файле. |
||||
произвести сеанс обмена немедленно, |
|
|||
или перенести сеанс на другое время. |
|
|||
Тогда расходы провайдера будут |
|
|||
определяться расходами на ожидание, |
|
|||
которые линейно зависят от времени, и |
|
|||
расходами на передачу данных, которые |
|
|||
зависят от значения величины |
|
|||
управления и объема передаваемых |
|
|||
данных.R |
=C(A − A |
)+T ϑ; 1≤i ≤N −1 |
|
|
|
||||
i |
i |
0 |
i |
|
Сеанс обмена может быть перенесен на N-1 интервал управления, при этом расходы от переноса вызова на i-й интервал будут равны
Часть рисунка с идентификатором отношения rId5 не найдена в файле.
223
Условия переноса трафика
Необходимое условие для переноса
сеанса
C(Ai − A0 )+Ti ϑ < C(Aj − A0 )+Tj ϑ; 1≤i ≤ N −1
Достаточное условие для переноса сеанса
C ( Ai − A0 ) + Ti ϑ < T0ϑ, 1≤i≤N − 1C ( Ai − A0 ) + Ti ϑ < C ( A j − A0 ) + T j ϑ, 1≤ j≤N − 1
Необходимое и достаточное условия для переноса сеанса
T − T |
i+1 |
|
T |
− T |
|||
max |
i |
|
, , |
i |
m |
||
A |
− |
A |
A |
− A |
|||
|
|
||||||
|
i+1 |
|
i |
|
m |
i |
|
i ≠ 0,i ≠m
|
|
T |
− T |
|
Ti−1 − Ti |
|
||
≤C<min |
0 |
i |
, , |
|
|
|
||
A |
− A |
A |
− A |
|||||
|
|
|
|
|||||
|
|
i |
0 |
|
i |
i−1 |
|
|
|
T0 − T1 |
|
T0 − Tm |
|
|
|
|
|
|||
|
|
||||
A − A |
|
|
|||
C≥max |
, , A |
− A |
, |
||
|
1 0 |
|
m |
0 |
|
|
1− S (µ0 ), |
i = 0 |
то сеанс не переносится |
||
Если P0i = S (νi ) − S (µi ), |
0 < i < m |
||||
|
|
|
|
|
|
|
|
i = m |
|
|
|
|
S (ν m ), |
|
|
||
224
Описание стоимости времени
Для множества услуг стоимость единицы времени - это случайная величина, имеющая некоторое распределение вероятности S(x).
|
|
|
|
Ti −Ti+1 |
|
|
Ti −Tm |
|
|
|
|
|
|||
|
|
|
|
, |
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
µi =max |
A |
−A |
A |
−A |
, 0≤i ≤m−1 |
|
||||||
|
|
|
|
|
i+1 |
i |
|
|
m |
i |
|
|
|
|
|
νi = min |
|
, , |
|
|
, |
0 |
≤ i ≤ m |
ϑ |
|
=ϑ P , 0≤k ≤m −1, 1≤i ≤N |
|||||
|
T0 −Ti |
|
Ti−1 −Ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ki |
|
k ki |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ai − A0 |
|
Ai − Ai−1 |
|
|
|
|
|
|
|
|
||||
Тогда объем данных, переносимых с кванта k на начало i-го участка управления, можно определить следующим образом:
Часть рисунка с идентификатором отношения rId10 не найдена в файле.
225
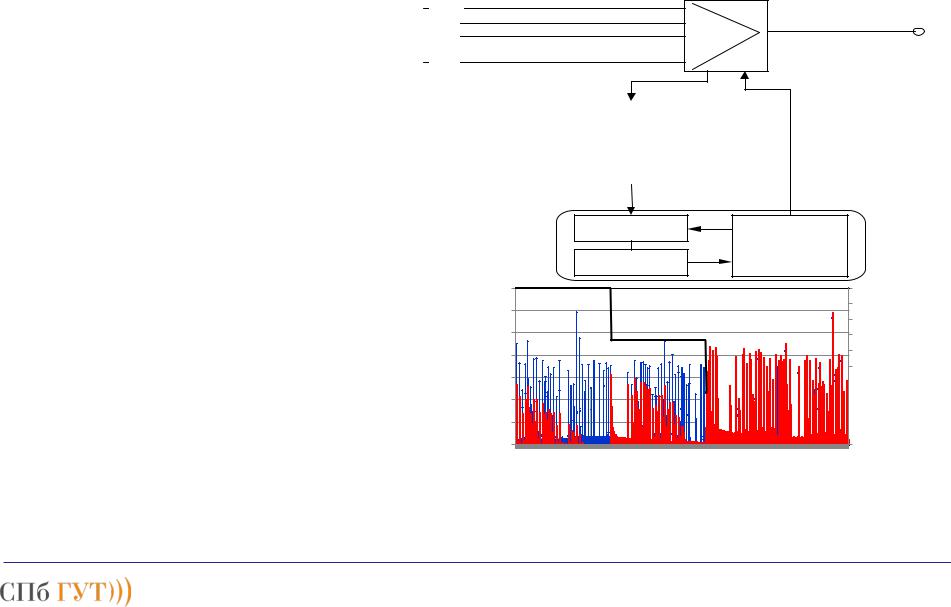
Пример оптимизации расписания управления
Для решения задачи 
оптимизации необходимо выбрать положение и число участков управления и определить соответствующие им значения величины управления, которые приводили бы к минимизации суммы целевой функции.
Для сокращения объема вычислений можно использовать методы спуска (подъема) с вычислением координат градиента, позволяющие учесть все ограничения.
НС 1
НС 2 НС 3
НС n
Объем данных байт
Исполнительное |
устройство |
Периодические |
|
|
Измерения |
|
|
потерь, |
Коэффициенты |
|
задержки, |
||
распределения |
||
джиттера, |
||
трафика |
||
полосы п. |
||
|
||
В каждом НС |
|
|
|
|
Параметры
модели
Модель системы
процедура
оптимизации
Критерий
70000
60000
50000
40000
30000
20000
10000
0 |
|
155 232 309 386 463 540 617 694 771 848 925 |
1 |
78 |
|
|
|
Номер кванта |
1
0,9
0,8
0,7
0,6
0,5 
0,4 
0,3 
0,2 
0,1
0
1002 1079 1156 1233 1310 1387 1464 1541 1618 1695 времени
Управляющее воздействие
|
|
Исходный рафик |
|
Трансформированный трафик |
|
|
Управляющее воздействие |
|
|
|
|
|
|
|
|
|
|
|
226