1
3
7 5
6
1
3
7 5
6
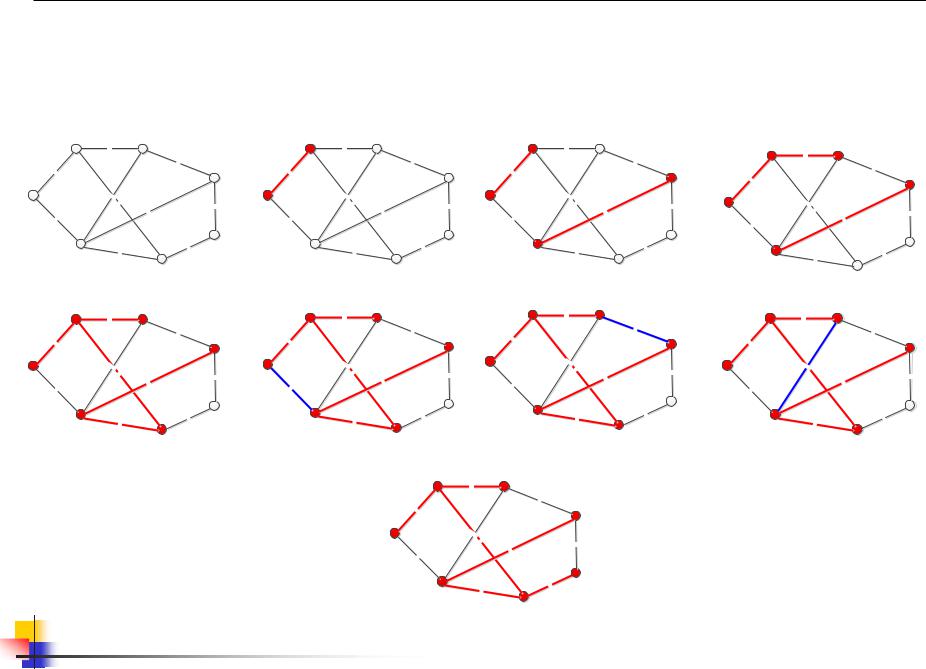
14.5 Пример алгоритма Краскала
(1,7)=3; (3,6)=3; (1,2)=4; (1,5)=4; (5,6)=4; (6;7)=5; (2,3)=6; (2,6)=6; (4,5)=6; (3,4)=7
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
3
7
4
3
7
4
1
3
7 5
6
1
3
7 5
6
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
1
3
7 5
6
3
7
4
3
7
4
1
3
7 5
6
1
3
7 5
6
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
3
7
4
3
7
4
3
7
4
1
3
7 5
6
1
3
5
6
4
6 |
4 |
|
|
|
4 |
4
6
4
2
6
3
6
5
2
6
3
6
5
3
7
4
3
7
4
109
14.5 Кратчайший остов (SST) графа (алгоритм Прима)
Шаг 1. Пусть Ts = {xs}, где хs — произвольно выбранная вершина, и Аs = (As является множеством ребер, входящих в SST).
Шаг 2. Для каждой вершины xj не принадлежащей Тs найти вершину aj принадлежащую Тs, такую, что
c(a j , xj ) = min[c(xi , xj )]= βj
x j TS
приписать вершине xj пометку [αjβj]. Если такой вершины αj нет, т. е. при Г (xj) ∩ Ts = , приписать вершине xj пометку [0, ∞].
Шаг 3. Выбрать такую вершину xj*, что βj* = min[βj ]
x j TS
Обновить данные: Ts = Ts U {xj*}, As = As U {(aj* , xj*)}.
Если | Ts | = n, то остановиться. Ребра в As образуют SST. Если | Ts | ≠ n, то перейти к шагу 4.
Шаг 4. Для всех хj Ts, таких, что хj Г (xj*), обновить пометки следующим образом. если βj > С (xj*, xj), то положить βj = С (xj*, xj), αj = xj* и вернуться к шагу 3.
если βj ≤ С (xj*, xj), то перейти к шагу 3.
110
1
3
7 5
6
1
3
7 5
6
1
3
7 5
6
1
3
7 5
6
2
|
4 |
|
|
|
|
|
6 |
|
6 |
4 |
|
|
|
|
|
|
|
|
3 |
|
|
4 |
6 |
|
|
|
|
|
|
|
5 |
|
|
|
2 |
4 |
|
|
|
|
|
|
6 |
6 |
4 |
|
|
|
|
||
|
|
|
3 |
|
|
4 |
6 |
|
|
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
5
3
7
4
3
7
4
3
7
4
3
7
4
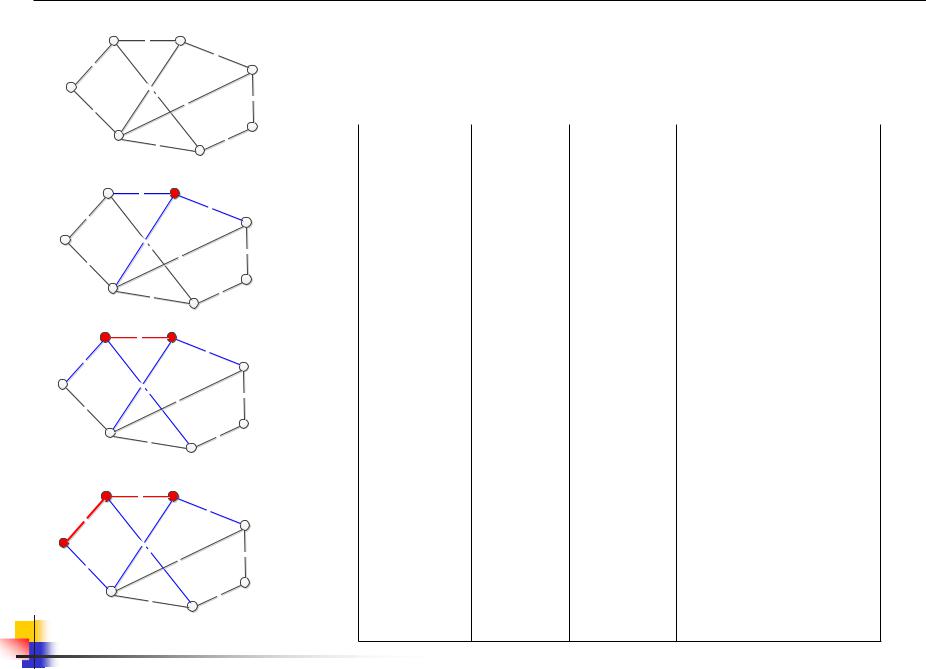
14.5 Пример алгоритма Прима |
|
|
|||
|
Ts={2} |
As= { } |
|
|
|
|
|
|
|
|
|
|
Ts |
Ts |
As |
Пометки вершин |
|
|
вершины |
ребра |
|
|
|
2 |
(1,2)=4 |
(1,2) |
1 |
[2, 4] |
|
|
|
(6,2)=6 |
|
3 |
[2, 6] |
|
|
(3,2)=6 |
|
4 |
[0, ∞] |
|
|
|
|
5 |
[0, ∞] |
|
|
|
|
6 |
[2, 6] |
|
|
|
|
7 |
[0, ∞] |
1,2 |
(7,1)=3 |
(1,2) |
3 |
[2, 6] |
|
|
|
(5,1)=4 |
(7,1) |
4 |
[0, ∞] |
|
|
(6,2)=6 |
|
5 |
[1, 4] |
|
|
(3,2)=6 |
|
6 |
[2, 6] |
|
|
|
|
7 |
[1, 3] |
|
|
|
|
|
|
1,2,7 |
(6,7)=5 |
(1,2) |
3 |
[2, 6] |
|
|
|
(5,1)=4 |
(7,1) |
4 |
[0, ∞] |
|
|
(6,2)=6 |
(5,1) |
5 |
[1, 4] |
|
|
(3,2)=6 |
|
6 |
[7, 5] |
111
1
3
7 5
6
1
3
7 5
6
1
3
7 5
6
1
3
7
6
2
4 |
|
|
|
|
|
|
6 |
6 |
4 |
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
6 |
|
|
|
|
|
|
2 |
5 |
|
|
|
|
4 |
|
|
|
|
|
|
6 |
6 |
4 |
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
6 |
|
|
|
5
2
4
|
|
6 |
6 |
4 |
|
|
|
|
|
|
3 |
|
4 |
6 |
|
|
|
|
|
5 |
|
|
2 |
|
4 |
|
|
4 |
|
|
|
3 |
|
4 |
6 |
|
|
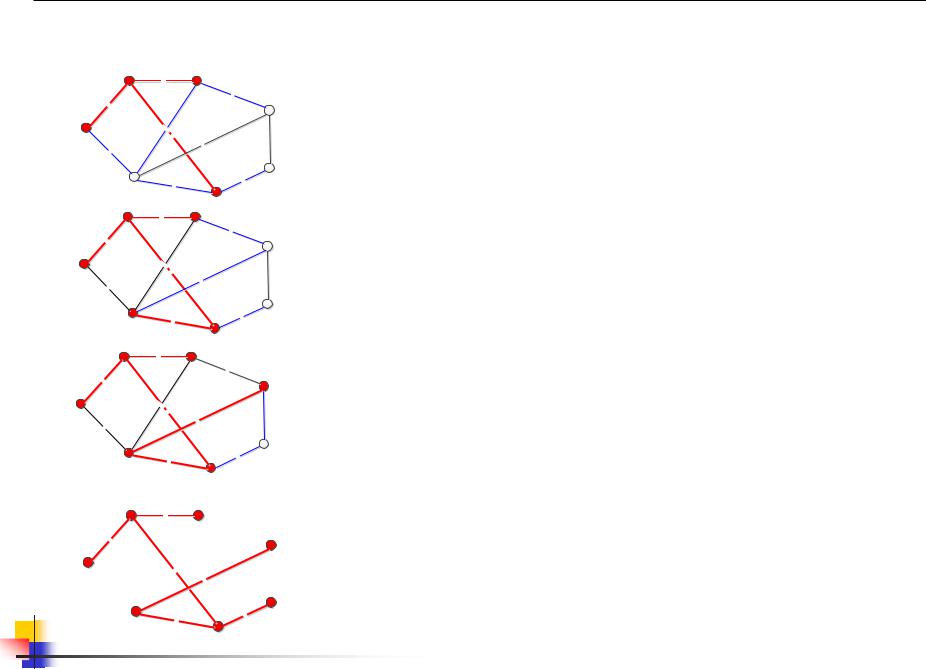
14.5 Пример алгоритма Прима (продолжение) |
|
|
|
||||||||
|
|
|
|
|
|
Ts |
Ребра |
|
As |
Пометки вершин |
|
3 |
1,2,5,7 |
(6,7)=5 |
|
(1,2) |
3 [2, 6] |
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(6,2)=6 |
|
(7,1) |
4 [0, ∞] |
|
7 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(6,5)=4 |
|
(5,1) |
6 [5, 4] |
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
(4,5)=6 |
|
(6,5) |
|
|
|||||
|
|
|
|
|
|
|
(3,2)=6 |
|
|
|
|
3 |
|
1,2,5,6,7 |
(3,6)=3 |
|
(1,2) |
3 [6, 3] |
|
||||
|
|
|
|
|
|
|
(3,2)=6 |
|
(7,1) |
4 [5, 6] |
|
|
|
|
|
|
|
|
(4,5)=6 |
|
(5,1) |
|
|
|
7 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(6,5) |
|
|
4 |
|
|
|
|
(3,6) |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2,3,5,6,7 |
(4,3)=7 |
|
(1,2) |
4 [4, 5] |
|
3 |
|
|
|
(4,5)=6 |
|
(7,1) |
|
|
|||
|
|
|
|
|
|
|
|
|
(5,1) |
|
|
|
|
|
|
|
|
|
|
|
(6,5) |
|
|
7 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(3,6) |
|
|
4 |
|
|
|
|
|
(4,5) |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2,3,4,5,6,7 |
|
|
(1,2) |
|
|
|
|
|
|
|
|
|
|
|
(7,1) |
|
|
3 |
|
|
|
(5,1) |
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
(6,5) |
|
|
|
|
|
|
|
|
|
|
|
(3,6) |
|
|
4 |
|
|
|
(4,5) |
|
112 |
|||||
|
|
|
|
|
|||||||
5