Рис. 84 Рис. 85 Точки на двух невесомых абсолютно твердых стержнях:

(x2 − x1)2 + (y2 − y1)2 = r22

x21 + y12 = r12

Кроме того, эти связи являются стационарными и голономными.

Определение. Если для некоторого возможного перемещения противоположное ему не является возможным, то связь называется неудерживающей (освобождающейся или односторонней). Удерживающие связи математически выражаются равенствами, а неудерживающие — неравенствами.

45.2Пример 2

Точка на нерастяжимой нити:

x2 + y2 + z2 ≤ r2

Рис. 86 Определение. Если в уравнение связи время не входит явно, то такая связь называется стацио-

нарной (склерономной):

f (xη, yη, zη) = 0.

здесь xη, yη, zη могут зависеть от t.

Определение. Если в уравнение связи время входит явно, то такая связь называется нестационарной (реономной):

f (xη, yη, zη, t) = 0

При стационарных связях действительное перемещение совпадает с одним из возможных перемещений. При нестационарной связи действительное перемещение может не совпадать ни с одним из возможных перемещений.

45.3Пример стационарной связи

Точка на поверхности

Рассмотрим точку (x, y, z) на поверхности:

Рис. 87

Пусть точка получила некоторое возможное перемещение:

M 0(x + δx, y + δy, z + δz).

Так как точка должна оставаться на поверхности, то приращения координат удовлетворяют равенству:

f (x + δx, y + δy, z + δz) = 0.

Разложим левую часть последнего уравнения в ряд Тейлора:

f (x, y, z) + ∂f∂x δx + ∂f∂y δy + ∂f∂z δz + ... = 0.

Здесь многоточием обозначены члены ряда, имеющие второй и более высокий порядок малости в сравнении с приращениями координат. С учетом выражения (131) получим:

∂f∂x δx + ∂f∂y δy + ∂f∂z δz = 0.

Так как возможным перемещением точки в данном случае является вектор δ~r, проекциями которого на оси координат являются δx, δy, δz, то последнее выражение можно переписать:

~ f · δ~r = 0. grad

~ f

Вектор grad направлен по нормали к рассматриваемой поверхности, а вектор возможного перемещения точки лежит в плоскости, касательной к поверхности в данной точке.

В случае стационарной связи действительное перемещение удовлетворяет уравнению:

df = ~ f · δ~r = 0. grad

Т.о., при стационарных связях действительное перемещение d~r совпадает с одним из возможных перемещений. При нестационарной связи действительное перемещение может не совпадать ни с одним из возможных перемещений.

45.4 Пример нестационарной связи

Точка на сфере переменного радиуса (нестационарная связь):

x2 + y2 + z2 = R2(t).

Определение. Связь называется геометрической, если в уравнение связи входят только координаты точек:

f (xη, yη, zη) = 0

Определение. Связь называется кинематической, если в уравнение связи входят координаты и скорости точек механической системы:

f (xη, yη, zη, vηx, vηy, vηz ) = 0

Определение. Связь называется голономной, если она выражается интегрируемым дифференциальным уравнением для координат и скоростей точек механической системы.

Замечание: Уравнение

называется интегрируемым, если существует функция F = F (xη, yη, zη, t), такая что уравнение (132) может быть записано в виде

dF

dt (xη, yη, zη, t) ≡ f (xη, yη, zη, vηx, vηy , vηz , t) = 0

Определение. Связь называется неголономной, если она выражается неинтегрируемым дифференциальным уравнением для координат и скоростей точек механической системы.

Определение. Связи, наложенные на механическую систему, называются идеальными, если сумма элементарных работ сил реакций этих связей на любом возможном перемещении равна нулю:

δ~rη = δrηxi + δrηyj + δrηz k

Согласно определению скалярного произведения двух векторов выражение (133) можно переписать

в виде:

Xn

(Rηxδxη + Rηyδyη + Rηz δzη) = 0

η=1

или

Xn ~

|Rη||δ~rη|cosαη = 0

η=1

где η — угол между векторами ~ η и η.

α R δ~r

Определение идеальных связей можно дать с использованием понятия мощности. Определение. Связи, наложенные на механическую систему, называются идеальными, если сум-

ма мощностей сил реакций этих связей равна нулю:

η=1

Согласно определению скалярного произведения двух векторов выражение (134) можно переписать в виде:

η=1

46Принцип Даламбера-Лагранжа (общее уравнение динамики)

Для системы с идеальными связями в любой момент времени сумма элементарных работ активных сил и даламберовых сил инерции равняется нулю:

Принцип Даламбера-Лагранжа можно сформулировать и с использованием понятия мощности:

Уравнения (135) и (136) называются общими уравнениями динамики

В случае равновесия механической системы ускорения всех точек системы равны нулю. Поэтому уравнения (135) и (136) принимают вид:

η=1

Уравнения (137) и (138) являются математическим выражение принципа возможных перемещений (возможных мощностей):

Для того, чтобы механическая система с идеальными (удерживающими) стационарными связями находилась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на любом возможном перемещении из предполагаемого состояния равновесия равнялась нулю.

47 Обобщенные координаты механической системы

Рассмотрим механическую систему из n точек, на которую наложены k удерживающих голономных связей. Тогда для 3n координат системы выполняются следующие условия:

f1(x1, y1, z1, x2, y2, z2, ..., xn, yn, zn, t) = 0,

f2(x1, y1, z1, x2, y2, z2, ..., xn, yn, zn, t) = 0,

...

fk(x1, y1, z1, x2, y2, z2, ..., xn, yn, zn, t) = 0.

Выберем первые k координаты и перенесем оставшиеся s = 3 · n − k в правые части уравнений. Далее разрешим полученные уравнения относительно первых k координат, а остальные s — переобозначим:

x1 = x1(q1, q2, ..., qs, t), y1 = y1(q1, q2, ..., qs, t), z1 = z1(q1, q2, ..., qs, t), x2 = x2(q1, q2, ..., qs, t),

...

...

xn = qs−2, yn = qs−1, zn = qs.

Таким образом, координаты всех точек системы будут функциями s независимых параметров системы и времени.

Определение. Независимые параметры, однозначно определяющие положение всех точек механической системы, называются обобщенными координатами этой системы. Число обобщенных координат является числом степеней свободы.

Систему можно записать в векторном виде:

Примеры:

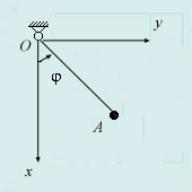
Пример 1: Плоский математический маятник:

Рис. 88

OA — невесомый абсолютно твердый стержень, O — цилиндрический шарнир. n = 1

Уравнения связей:

x2A + yA2 + zA2 = R2; zA = 0(k = 2) S = 3 · n − k = 1

Если за обобщенную координату выбрать, то имеем следующие уравнения:

xA = R cos ϕ; yA = R sin ϕ; zA = 0

Пример 1: Точка M на поверхности сферы: n = 1, k = 1.

Уравнение связи: x2 + y2 + z2 = R2

S = 3 · n − k = 2

Если за обобщенные координаты выбрать γ (широту) и ϕ (долготу), то имеем следующие уравнения:

Уравнения (140) определяют траекторию некоторой точки в s-мерном пространстве. Пространство q1, q2, ..., qs называется конфигурационным пространством механической системы. Изучение движения механической системы можно свести к нахождению траектории изображающей точки в конфигурационном пространстве.

Рассмотрим точку M 0, положение которой определяется как

M 0(q1 + δq1, q2 + δq2, ..., qs + δqs)

δq1, δq2, ..., δqs — вариации обобщенных координат Положению точки M 0 соответствует радиус-вектор

~rη0 = ~rη0 (q1 + δq1, q2 + δq2, ..., qs + δqs, t); η = 1, 2, ..., n

При перемещении изображающей точки в точку 0 (в конфигурационном пространстве) точка с массой mη механической системы совершает перемещение

Выражение (141) устанавливает связь между возможными перемещениями точек механической системы и вариациями обобщенных координат.

Вычислим элементарную работу активных сил на возможном перемещении, определяемом выражением (141) :