Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «МЭИ»
Предмет:
Теоретическая механика
Файл:
Краткий курс лекций.pdf
Скачиваний:
468
Добавлен:
27.05.2014
Размер:
1.19 Mб
Скачать
☆
►Содержание►

~e

~i

— равнодействующие всех внешних и внутренних сил, действующих на данную точку.

где Fk

, Fk

Составляя такие уравнения для всех точек системы и складывая их почленно, получим

 

 

 

 

 

n

 

n

 

 

n

 

 

 

 

 

d

X

~

X

~ ~e

 

X

~ ~i

 

 

 

 

 

 

 

 

 

 

 

 

 

[

 

MO(mkv~k)] =

 

MOFk

+

 

MOFk

,

 

 

dt

k=1

 

k=1

 

 

k=1

 

 

Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда, учитывая равенство

n

 

 

K~O = Pk=1 M~O(mkv~k) найдем окончательно

n

 

 

d

~

X

~ ~e

 

 

KO =

 

MOFk

 

dt

k=1

 

 

 

 

 

Полученное уравнение выражает следующую теорему моментов для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра.

Проектируя обе части равенства на неподвижные оси Oxyz, получим:

 

 

n

 

 

 

n

 

 

 

n

d

 

X

 

d

 

X

 

d

 

X

 

KOx =

 

MOxFkxe ,

 

KOy =

 

MOyFkye ,

 

KOz =

MOz Fkze

dt

k=1

 

dt

k=1

 

dt

k=1

 

 

 

 

 

 

 

 

Уравнения выражают теорему моментов относительно любой неподвижной оси.

37 Принцип Даламбера

Рассмотрим движущуюся материальную точку. На точку кроме приложенной активной силы могут действовать реакции связи

 

~ (a)

 

 

 

 

 

 

 

F

µ

 

 

 

 

 

 

 

~a

 

~

 

 

 

 

 

 

-

R

 

 

 

 

m

 

-

 

 

 

 

 

 

 

 

 

 

 

~ (a)

~

(108)

 

 

 

 

m~a = F

+ N

 

~ R

 

~ (a)

 

~

 

 

 

 

F

+ N + (−m~a) = 0

(109)

 

N

 

 

 

~

 

(110)

 

 

 

 

 

Φ = −m~a

Формулой (110) определяется сила инерции(Даламберова сила)

 

 

 

 

 

~ (a)

~

~

(111)

 

 

 

 

F

 

+ N + Φ = 0

Из формулы (111) следует принцип Даламбера для одной материальной точки:

•активные силы, реакции связи и силы инерции образуют уравновешенную систему или систему сил эквивалентную нулю.

Используя формулу (111) мы сможем свести задачу динамики к задаче элементарной статики.

38 Принцип Даламбера для системы материальных точек

Рассмотрим произвольную систему n материальных точек к которым приложены активные (известные) силы и на которые наложены произвольные связи.

z 6

~

O

~av

 

 

Fv

 

 

 

 

µ

 

 

mv

 

 

 

 

*

z

~

O

 

~rv

-

Nv

ª

 

 

y

 

 

 

 

 

x

 

 

 

 

Рис. 77 На основании аксиомы о связях освободим систему от связей и заменим их действие реакциями.

Уравнения движения будут иметь вид:

 

~ (a)

~

 

 

~

= 0

 

 

F1

 

+ N1

+ Φ1

 

 

~ (a)

~

 

 

~

= 0

 

 

F2

 

+ N2

+ Φ2

 

 

 

........................

 

 

 

~ (a)

~

 

 

~

 

 

 

 

Fn

 

+ Nn

+ Φn = 0

 

n

 

 

 

n

 

 

 

n

 

 

X

~

(a)

 

X

~

X

~

= 0

 

Fi

+ Ni +

 

Φi

i=1

 

 

 

i=1

 

 

i=1

 

 

Из (112) получаем:

~

 

 

~ (N )

~ (инерц)

 

 

(a)

 

 

 

R

 

+ R

 

 

+ R

 

 

 

~

R(a) — главный вектор активных сил;

~

R(N ) — главный вектор сил реакций связей;

~

R(инерц) — главный вектор даламберовых сил инерции.

Из (113) следует принцип Даламбера для системы материальных точек:

(112)

(113)

•Сумма главных векторов активных сил, реакций связи и сил инерции равна нулю, т.е. активные силы и реакции связи и силы инерции образуют уравновешенную систему сил.

39Главный вектор и главный момент даламберовых сил инерции

Так как главный вектор даламберовых сил инерции равен

 

 

 

 

n

 

 

n

~

~

 

 

 

 

~

(инерц)

X

 

 

X

mv

dVv

 

dQ

 

 

 

R

 

= −

mv~av = −

 

= −

 

 

(114)

 

 

 

dt

dt

 

 

 

 

v=1

 

 

v=1

 

 

 

 

 

 

 

~

n

 

~ (инерц)

~

 

 

 

 

 

 

 

 

 

dQ

, т.е главный вектор даламберовых сил инерции

здесь Q =

v=1 mv~vv. Таким образом, R

 

= − dt

равен

производной по времени от вектора количества движения системы материальных точек, взятый

 

P

 

 

 

 

 

 

 

 

 

 

 

с обратным знаком.

Вектор количества движения системы материальных точек как функция скорости центра масс

~

 

 

 

имеет вид: Q = m~vc. Поэтому

 

d~vc

 

~ (ин)

 

 

R

= −m

 

(115)

dt

•Главный вектор сил инерции системы материальных точек равен силе инерции центра масс системы в предположении, что в нем сосредоточена вся масса системы

Главный момент относительно точки О даламберовых сил инерции системы материальных точек имеет вид:

 

 

~

 

 

~

(a)

~ (N )

~ (инерц)

 

(116)

 

 

L0

= L0

+ L0

 

+ L0

 

 

или

 

 

 

 

n

 

 

 

n

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

X

~ (a)

+

X

 

~ (N )

+

X

~

(инерц)

= 0

(117)

 

~rvFv

 

 

~rv Nv

 

~rvΦv

 

v=1

 

 

 

 

v=1

 

 

v=1

 

 

 

 

Где момент инерции имеет вид:

 

n

 

 

 

n

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

 

P

 

L~ (инерц) =

X

~r Φ~

 

=

X

 

 

 

 

 

 

 

 

 

 

 

 

d~vv

=

d

~rv × mv~vv

 

 

 

~r

m

~a

 

=

−

~r

×

m

 

 

 

 

−

0

v=1

v

v

 

v=1

v ×

v

 

v

 

v

 

 

v dt

 

dt

В последнем выражении векторное произведение

d~rv

 

× mv~vv равно нулю, а

dt

количества системы относительно точки . Поэтому

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~ (инерц)

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dK0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L0

 

= −

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

 

+ X d~rdtv × mv~vv

P ~rvmv × ~vv — момент

(118)

•главный момент даламберовых сил инерции системы материальных точек относительно точки равен производной по времени от вектора кинетического момента этой системы относительно точки с противоположным знаком.

40 Оси Кенига

Рассмотрим систему материальных точек с массами mv и координатами xv, yv , zv в неподвижной системе координат Ox*y*z*.

z*6

z

 

6

c-

 

ª

y

 

 

 

x

 

O

*

- y*

ª

 

x

 

Рис. 78 Координаты центра масс этой системы определяются равенствами:

xc =

P mv

; yc =

P mv

; zc =

P mv

(119)

 

mvxv

 

mvyv

 

mvzv

 

 

P

 

P

 

P

 

Если в центре масс построить систему осей Cxyz, которые параллельны осям Ox*y*z* и перемещаются поступательно относительно этих (неподвижных) осей, то такая система осей будет называться осями Кенига.

41Кинетический момент абсолютно твердого тела относительно неподвижной точки

Разобьем тело на n материальных точек с массами mν

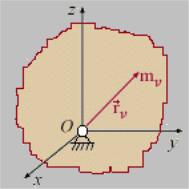
Рис. 79 По определению кинетического момента:

 

 

 

 

 

 

n

 

n

 

 

 

 

 

 

 

 

 

~

 

X

~

X

 

~

 

 

 

 

 

 

 

KO =

KOν

=

r~ν × mν Vν

 

 

(120)

 

 

 

 

 

 

ν=1

 

ν=1

 

 

 

 

 

Скорость любой точки тела выражается как:

 

 

 

 

 

 

 

 

 

 

 

~

 

~

 

 

~

 

 

 

 

 

 

 

 

Vν = VO + ω~ × r~ν , где VO = 0

 

 

 

С учетом последнего

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

n

 

 

 

 

 

 

 

~

X

 

 

 

 

X

 

 

 

 

 

 

 

KO =

 

r~ν × mν ω~ × r~ν =

mν (ω~(r~ν · r~ν ) − r~ν r~ν · ω~)

 

 

 

 

 

ν=1

 

 

 

 

ν=1

 

 

 

 

 

Запишем векторы из предыдущего выражения как функции их проекций на оси координат:

 

~

~

~

 

~

 

 

~

~

~

~

~

~

 

KO = KOxi + KOyj + KOz k; r~ν = xν i + yν j + zν k; ω~ = ωxi + ωyj + ωz k

Учтем, что r~ν · r~ν = xν2 + yν2 + zν2;

r~ν · ω~ = xν ωx + yν ωy + zν ωz

 

 

 

 

Тогда выражение примет вид:

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

~

X

~

~

~

2

 

2

2

~

~

~

+ yν ωy + zν ωz )}

KO =

 

mν {(ωxi + ωyj + ωz k)(xν

+ yν + zν ) − (xν i + yν j + zν k)(xν ωx

ν=1

Для проекций вектора кинетического момента получаем выражения:

Xn

KOx = mν {ωxx2ν + ωxyν2 + ωxzν2 − x2ν ωx − xν yν ωy − xν zν ωz }

ν=1

Xn

KOy = mν {ωy x2ν + ωyyν2 + ωyzν2 − xν yν ωx − yν2ωy − yν zν ωz }

ν=1

Xn

KOz = mν {ωz x2ν + ωz yν2 + ωz zν2 − zν xν ωx − yν zν ωy − zν2ωz }

ν=1

Поскольку не зависят от выбора точки на теле, то предыдущие выражения можно переписать в виде:

n

 

n

n

 

X

 

X

X

 

KOx = [ mν (yν2 + zν2)]ωx − [ mν xν yν ]ωy − [

mν xν zν ]ωz

ν=1

 

ν=1

ν=1

 

n

n

 

n

 

X

X

 

X

KOy = −[

mν yν xν ]ωx + [

mν (zν2 + xν2 )]ωy − [

mν yν zν ]ωz

ν=1

ν=1

 

ν=1

n

n

 

n

 

X

X

 

X

 

KOz = −[

mν zν xν ]ωx − [

mν zν yν ]ωx + [

mν (xν2 + yν2)]ωz

ν=1

ν=1

 

ν=1

 
Соседние файлы в предмете Теоретическая механика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности