Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «МЭИ»
Предмет:
Теоретическая механика
Файл:
Краткий курс лекций.pdf
Скачиваний:
468
Добавлен:
27.05.2014
Размер:
1.19 Mб
Скачать
☆
►Содержание►

43 Кинетическая энергия

43.1Кинетическая энергия материальной точки

Определение. Кинетическая энергия материальной точки — скалярная мера механического движения, равная:

miv2

Ti = i

2

т.е. половина произведения массы точки на квадрат ее скорости.

43.2 Кинетическая энергия системы материальных точек

Определение. Кинетическая энергия системы n материальных точек равна сумме кинетических энергий всех точек:

n

n

mivi2

X

X

 

T =

Ti =

 

i=1

i=1

2

 

• Теорема Кенига:

Кинетическая энергия системы материальных точек в ее абсолютном движении складывается из кинетической энергии центра масс системы, в предположении, что в нем сосредоточена масса всей системы, и кинетической энергии системы в ее движении относительно центра масс.

Доказательство.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

0

0

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i=1 mi~ri

 

 

 

 

Cx

y

z

 

— кенигова система координат, так как ~ri

 

=

 

 

 

 

 

 

 

— радиус-вектор центра масс

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P i=1 mi

 

 

 

 

системы. Поэтому

 

 

 

 

 

 

 

 

 

 

 

n

 

mi~r0

 

 

 

 

 

P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~r0 =

 

i=1

 

 

 

i

= 0

 

 

 

 

 

 

 

 

 

 

(129)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P i=1 mi

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

 

 

 

 

 

 

d~r0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~viабс = ~viотн + ~viпер =

 

 

i

+ ~vC

 

 

 

(130)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выражение для кинетической энергии системы имеет вид:

 

 

 

 

 

 

!

 

 

 

 

 

 

 

 

 

 

 

 

 

T = 2

 

mi ~vi

 

 

 

= 2

 

 

 

mi à dt + ~vC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

n

 

абс 2

 

 

 

1

n

 

 

 

 

 

d~ri0

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X

³

´

 

 

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i=1

 

 

 

 

 

 

 

 

i=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

или

 

 

 

T = 2 i=1 mi

à dt

!

2

+ i=1 mi

dt · ~vC + 2 i=1 mi

(~vC )2 = 2 i=1 mi(~vi )2 +

2~vC

i=1 mi

 

 

 

 

 

1 n

d~r0

 

 

n

 

d~r0

 

1

 

n

 

 

 

 

 

 

 

 

 

 

 

1 n

 

1

 

n

 

 

 

 

 

 

X

 

i

 

 

 

X

i

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

 

 

 

X

отн

 

2

X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Так как

 

 

 

 

 

 

n

 

 

d~r0

 

n

d~r0

 

 

 

 

 

 

 

 

d

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

 

 

 

mi

i

· ~vC = mi

i

· ~vC =

 

Ã

 

 

mi~ri0 · ~vC ! = 0

 

 

 

 

 

 

 

 

 

 

 

dt

dt

dt

 

 

 

 

 

 

 

 

 

 

 

 

i=1

 

 

 

 

 

 

i=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i=1

 

 

 

 

(см (129)). Поэтому

T = 12 mvC2 + T отн

Что и требовалось доказать.

43.3Кинетическая энергия абсолютно твердого тела при поступательном движении

По определению кинетической энергии механической системы

T = 1 Xn miv2

2 i=1 i

Но при поступательном движении все точки тела имеют равные скорости ~vi = ~v , поэтому:

1

n

v2

n

 

mv2

 

 

X

 

X

 

 

T =

 

mivi2 =

 

 

mi =

 

2 i=1

2 i=1

2

или

T = mv2

2

43.4Кинетическая энергия абсолютно твердого тела при вращении вокруг неподвижной оси

Для любой точки тела vi = ωhi , поэтому

 

 

1 n

ω2

n

 

 

ω2

n

 

 

 

 

X

 

 

X

 

 

 

 

X

 

 

T =

 

 

mivi2 =

 

 

mihi2 =

 

mi(xi2 + yi2)

 

 

2 i=1

2

i=1

2

i=1

т.е.

 

 

 

 

 

 

 

Izzω2

 

 

 

 

 

 

 

T =

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

n 2

2

) — осевой момент инерции тела.

 

где Izz = Pi=1(xi

+ yi

 

 

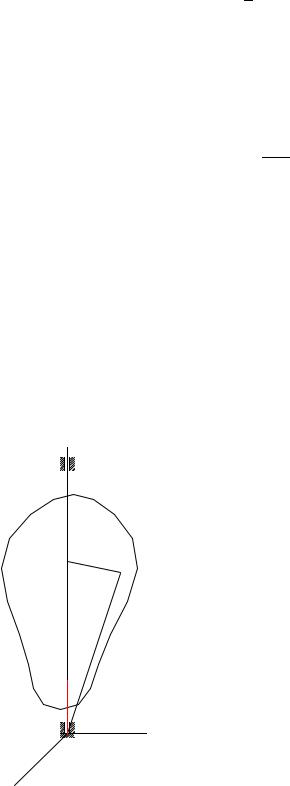
z

 

 

6

 

 

hi

mi

 

 

±

 

~ri

 

ω~

6

 

 

 

O

 

-y

xª

Рис. 83

44 Работа и мощность сил

Определение. Элементарным перемещением точки называется бесконечно малое перемещение, равное дифференциалу радиуса вектора точки.

Определение. Элементарной работой силы на перемещении называется скалярное произведение вектора силы на вектор элементарного перемещения точки приложения силы:

Определение. Мощностью силы называется скалярное произведение вектора силы на вектор скорости точки приложения силы:

~

N = F · ~v

или

~

N = |F ||~v| cos α = Fxvx + Fyvy + Fz vz

Данное определение согласуется с определением мощности, как работе в единицу времени:

 

dA

 

dx

 

dy

dz

 

N =

 

 

= Fx

 

 

+ Fy

 

+ Fz

 

= Fxvx + Fyvy + Fz vz

dt

dt

dt

dt

Мощность системы сил, приложенных к абсолютно твердому телу, равна сумме мощностей всех сил:

 

 

 

n

 

n

 

 

 

 

 

 

 

 

 

X

 

X

~

 

 

 

 

 

N =

Nη =

 

Fη · ~vη

 

 

 

 

 

 

η=1

 

η=1

 

 

 

 

 

но ~vη = ~v0 + ~ω × ~r, поэтому

 

n

 

 

 

 

 

 

 

 

 

 

 

X

~

 

 

 

 

 

 

 

 

 

N =

Fη · (~v0 + ω~ × ~r)

 

 

 

 

 

 

η=1

 

 

 

 

 

 

 

 

n

 

n

 

 

 

n

 

 

n

 

X

~

X

~

 

X

~

 

X

~

N = Fη · ~v0

+ (Fη · [~ω × ~r]) = (

 

 

Fη · ~v0) +

η=1

(ω~ · [~r × Fη])

η=1

 

η=1

 

 

η=1

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

~

X

~

 

 

~

 

~

 

 

N = R · ~v0

+ ω~ ·

~r × Fη

= R · ~v0

+ ω~ · L0.

 

 

 

η=1

 

 

 

 

 

 

 

Таким образом,

 

 

~

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N = R · ~v0

+ ~ω · L0

 

 

 

Т.е., мощность системы сил, приложенных к абсолютно твердому телу, равна сумме скалярных произведений главного вектора на скорость полюса О и главного момента сил относительно полюса О на вектор угловой скорости твердого тела.

См. также частные случаи для вычисления мощности:

44.1Поступательное движение абсолютно твердого тела

~

~

принимает вид:

При поступательном движении выражение для мощности N = R · ~v0

+ ~ω · L0

~

 

 

N = R · ~v,

 

 

так как вектор угловой скорости равен нулю и скорости всех точек тела одинаковы.

44.2Вращение абсолютно твердого тела вокруг оси, проходящей через точку

О

При вращении твердого тела вокруг оси, проходящей через точку O, скорость точки O равна нулю

 

~

~

принимает вид:

и поэтому выражение для мощности N = R · ~v0

+ ~ω · L0

~

· ω~ = L0xωx

+ L0yωy + L0z ωz = L0z ωz

N = L0

так как ωx = 0, ωy = 0

44.3Система сил приводится к равнодействующей, приложенной в точке O

~

~

принимает

В этом случае главный момент равен нулю и выражение для мощности N = R ·~v0

+ (ω~ ·L0

вид:

 

 

~

 

 

N = R · ~v0

 

 

Замечание: Равнодействующая равна главному вектору.

 

 

44.4 Система сил приводится к паре сил

~

~

принимает

Так как система сил приводится к паре, выражение для мощности N = R · ~v0

+ ω~ · L0

следующий вид:

 

 

~

 

 

N = L · ω~

 

 

~

 

 

здесь L — момент пары сил.

 

 

45 Связи и ограничения на движение твердых тел

Определение. Связями называются ограничения, накладываемые на координаты и скорости точек механической системы, которые выполняются при любых действующих на систему силах.

Конструктивно связи реализуются при помощи шарниров, стержней, нитей, поверхностей и т.п. Математически связи выражаются в виде уравнений или неравенств, содержащих координаты и скорости точек системы и время:

fi(~r1, ~r2, ..., ~rn, ~v1, ~v2, ..., ~vn, t) ¦ Fi

Здесь i =1,2,... k (количество связей, наложенных на систему), знак ¦ обозначает один из знаков: =,<,>; ~r1, ~r2, ..., ~rn — радиусы-векторы, а ~v1, ~v2, ..., ~vn - скорости точек системы.

Определение. Возможным перемещением точки называется бесконечно малое воображаемое перемещение точки, допускаемое связями в данный момент времени:

~

~

~

δ~rη = δxη i

+ δyηj

+ δzηk

Здесь δxη , δyη, δzη - проекции вектора δ~rη на оси координат.

Определение. Возможной скоростью называется отношение возможного перемещения к некото-

рому мыслимому интервалу времени:

E δ~rη ~vη = dt0

Возможная скорость — это скорость, которую бы имела точка, если бы она совершала возможное перемещение за время dt’.

Определение. Если для любого возможного перемещения противоположное ему тоже является возможным, то связь называется удерживающей (неосвобождающейся или двусторонней).

45.1 Пример 1

Точка на невесомом абсолютно твердом стержне (маятник): x2 + y2 + z2 = r2

Соседние файлы в предмете Теоретическая механика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности