Формирование м. Д. Н. Ф.

Перейдем к описанию метода построения м. д. н. ф. из простых импликантов для произвольной функции f. Обозначим через A1, А2,…,АS все простые импликанты функции f. Будем говорить, что импликанты А_i1, А_i2,…., А_it образуют покрытие функции f, если А_i1 VА_i2 V …. V А_it = f.

В частности, все простые имплнканты функции f, а так же импликанты, входящие в некоторую ее м.д.н.ф., образуют покрытия. Покрытие назовем неизбыточным, если при удалении из него произвольного импликанта оно перестает быть покрытием. Так, множество импликантов, входящих в м.д.н.ф. или в кратчайшую д. н. ф., образует неизбыточное покрытие. Ниже будет указан способ нахождения всех неизбыточных покрытий. Из них затем могут быть выбраны покрытия, которым соответствуют м. д. н. ф.

Будем говорить, что конъюнкция К покрывает набор ά, если на наборе ά она обращается в 1. Заметим, что в этом случае представляющий набор конъюнкции получается из ά заменой некоторых компонент прочерками. Так, например, конъюнкция x1x3, задаваемая набором 1 - 0 -, покрывает наборы 1OOO, 1001, 1100 и 1101. Ясно, что множество импликантов образует покрытие функции f тогда и только тогда, когда для каждого набора ά такого, что f(ά)=1, в этом множестве содержится импликант, покрывающий ά. Построим по функции f импликантную таблицу. Ее строки соответствуют единичным наборам функции f, а столбцы - простым импликантам. В пересечении строки ά и столбца Аi; проставляется *, если импликант Аi покрывает набор ά (в противном случае клетка оставляется пустой), Множество импликантов образует покрытие функции f, если столбцы, соответствующие имиликантам этого множества, содержат * в каждой строке.

Вкачестве примера рассмотрим функцию f(x1,x2,x3,x4), задаваемую таблицей 2.8. Как мы видели (см. табл. 2.9), ее простыми импликантами являются конъюнкции A1 == x1x2x4, А2=x2x3, А3=x3x4, A4=x2x4 и A5=x1x3.

Импликантная таблица функции f приведена в таблице 2.10.

С импликантом Аi, будем связывать логическую переменную аi: (принимающую значения 0 и 1). Каждому множеству импликантов приписывается набор значений

Таблица 2.10

Вектора, На которых F=1	А1 x1x2x4	А2 x2x3	А3 x3x4	А4 x2x4	А5 x1x3
0000		*	*
0001		*		*
0011				*
0100	*		*
0110	*
1000		*	*		*
1001		*		*	*
1011				*
1100			*		*
1101					*

переменных ai: если импликант Ai входит в множество, то ai = 1, если нет, то

ai=0. Рассмотрим строку таблицы покрытий, соответствующую некоторому набору ά. Пусть в этой строке символы * находятся в столбцах А_i1, А_i2,…., А_iv.

Строка ά будет покрытой тогда и только тогда, когда в множество включен хотя бы один из импликантов А_i1, А_i2,…., А_iv , т. е. когда дизъюнкция

a_i1 Va_i2 V …. V a_iv равна 1. Составим такую дизъюнкцию для каждой строки импликантной таблицы и возьмем их произведение по всем строкам. Полученную функцию обозначим через F. В частности, функция,

соответствующая таблице 2.10, имеет вид

F = (а2Va3) (а2Vа4)а4(a1Va3)a1(a2Va3Va5)& (a2Va4Va5)a4(a3Va5).

Множество импликаптов образует покрытие тогда и только тогда, когда набор значений переменных аi, соответствующий этому покрытию, обращает функцию F в единицу, ибо равенство F=1 имеет место тогда и только тогда, когда все скобки равны 1, т. с. когда все строки покрыты.

Преобразуем формулу, задающую функцию F. Вначале с использованием правила поглощения (Ф1VФ2)Ф1=Ф1 удалим более длинные скобки (т.е. такие, что из них вычеркиванием некоторых членов можно получить другие скобки). Затем на основе свойства дистрибутивности раскроем все скобки, в результате чего получим выражение вида дизъюнкции конъюнкций. И, наконец, пользуясь правилом поглощения Ф1VФ1Ф2=Ф1, удалим более длинные конъюнкции

(т. е. такие, что из них вычеркиванием некоторых переменных можно получить другие конъюнкции). В результате придём к представлению

F = V a_i1a _i2… a _ip,

(i₁, i₂,…, i_p)?I

в котором отсутствуют поглощения конъюнкций (дизъюнкция берется по некоторому множеству I наборов (i₁, i₂,…, i_p). По следствию 1 к теореме 2.2 (функция F является монотонной, а по следствию 2 представление (2.11) совпадает с м.д.н.ф. и является дизъюнкцией всех простых импликантов). Отсюда вытекает, что функция F имеет единственное представление вида (2.11).

Осуществим указанные преобразования применительно к функции F из рассматриваемого примера. Вычеркивание более длинных скобок дает выражение F =(a2Va3)а4а1а5. Раскрывая скобки, получаем представление вида (2.11)

F = а1а2а4а5 V а1а3а4а5. (2.12)

Теорема 2.3. Всякой конъюнкции a_i1a _i2… a _ip, входящей в представление (2.11) функции F, соответствует неизбыточное покрытие {A_i1A _i2… A_ip} функции f и, наоборот, всякому неизбыточному покрытию {A_i1A _i2… A_ip} соответствует конъюнкция a_i1a _i2…a _ip представления (2.11).

Доказательство.

Рассмотрим произвольную конъюнкцию a_i1a _i2… a _ip из представления (2.11).

Согласно сказанному выше она является простым импликантом функции F.

Полагая a_i1=a _i2=_…=a _ip=1, остальные переменные равными 0, получаем F = 1.

Отсюда заключаем, что множество {A_i1A_i2…A_ip}образует покрытие. Предположим, что оно избыточно и при удалении из A_ip, например, снова получается покрытие. Тогда на наборе a_i1=a_i2=_…=a_ip-1=1, a_i=0 (i?i₁,… i_p-1) функция F обращается в 1. В силу монотонности она равна 1 и на всяком другом наборе, где a_i1=a_i2=_…=a_ip-1=1 . Поэтому конъюнкция a_i1=a_i2=_…=a_ip-1 является импликантом, а это противоречит тому, что импликант a_i1=a_i2=_…=a_ip простой. Таким образом, покрытие {A_i1A_i2…A_ip} неизбыточно.

Обратно, пусть имеется неизбыточное покрытие {A_i1A_i2…A_ip}.

Полагая a_i1=a_i2=_…=a_ip=1, а остальные переменные равными 0, получаем F=1 (поскольку {A_i1A_i2…A_ip}- покрытие). В силу монотонности F обращается в 1 на всех наборах, где a_i1=a_i2=_…=a_ip=1. Поэтому a_i1…a_ip является импликантом. Если бы он не был простым, и в нем можно было вычеркнуть, например, a_ip, то на наборе a_i1=a_i2=_…=a_ip-1=1 функция F равнялась бы 1 и множество

{A_i1A_i2…A_ip-1}образовывало бы покрытие. Это противоречит неизбыточности покрытия {A_i1A_i2…A_ip}.

Теорема доказана.

Таким образом, представление (2.11) задает все неизбыточмые покрытия функции f. Из них могут быть выбраны покрытия, соответствующие м.д.н.ф.

Продолжим рассмотрение примера. Представление (2.12) показывает, что имеются 2 неизбыточных покрытия: {A1,А2,А4,А5} и {A1,А3,А4,А5}. Им соответствуют д.н.ф., содержащие по 9 вхождений символов переменных, поэтому каждая из них является минимальной.

Таким образом, f имеет две м. д. н. ф.:

f= A1VA2V A4VA5=x1x2x4Vx2x3Vx2x4Vx1x3,

f= A1VA3V A4VA5=x1x2x4Vx3x4Vx2x4Vx1x3.

Построение кратчайших д.н.ф. осуществляется тем же способом. Им соответствуют неизбыточные покрытия наименьшей мощности и, следовательно, конъюнкции представления (2.11) наименьшей длины.

Изложенный способ построения м. д. н. ф. хорошо иллюстрирует подход к отысканию оптимальных решений, основанный на сокращении перебора. Тривиальный способ нахождения м.д.н.ф. связан с просмотром всех д. п. ф. в порядке возрастания их сложности вплоть до д. н. ф., реализующей исходную функцию f. Теорема 2.1 позволила существенно сократить поиск, ограничившись д. н. ф., составленными только из простых импликантов функции f. Дальнейшее уменьшение вариантов осуществлено за счет выделения тех из них, которые соответствуют неизбыточным покрытиям. В результате их полного просмотра находится минимальное решение.

С ростом числа аргументов число неизбыточных покрытий для абсолютного большинства функций растет чрезвычайно быстро ([11], раздел 3), поэтому описанный метод минимизации применим лишь к функциям от небольшого числа аргументов.

При большом числе аргументов наиболее трудоемким является этап, связанный с отысканием наилучшего покрытия (система простых импликантов находится сравнительно просто). Для осуществления этого этапа обычно используются приближенные методы, не гарантирующие минимальности построенной д. н. ф. Одни из них состоит в следующем. Если в импликантной таблице имеются строки, содержащие по одному символу* (см. строки 0011, 0110, 1011 и 1101 табл. 2.10), то покрывающие их импликанты (в данном случае А4, А1, A5) входят в любую д. н. ф. Они включаются в покрытие и соответствующие им столбцы, и покрываемые ими строки вычеркиваются из таблицы. Дальнейший выбор импликантов осуществляется с использованием следующей пошаговой процедуры. В новой таблице берется столбец с наибольшим числом символов * (если таких столбцов несколько, то любой из них). Этот столбец и строки, в которых он содержит *, из таблицы вычеркиваются, а соответствующий импликант включается в покрытие. К полученной таблице применяется та же операция и т. д., пока все строки не окажутся

Таблица 2.14

	А1	А2	А3	А4	А5	А6	А7
0100	*	*
0110	*	*	*
1010				*
1111					*	*	*

Импликантная таблица для данного примера приведена в таблице 2.14. Образуем функцию

F == (a1Va2) (a1Va2Va3) a4(a5Va6V a7).

Вычеркивая (а1Va2Vа3) и раскрывая скобки, получаем 6 различных конъюнкций длины 3. Каждой из них соответствует неизбыточное покрытие, приводящее к д. н. ф. с б вхождениями символов переменных. Все эти д. н. ф. являются минимальными. Примером м. д. н. ф. может служить

f =A1VA4VA5=x1x4Vx2x3Vx3x4.

На практике построение д. н. ф. обычно является промежуточным этапом, после чего осуществляется упрощение формулы путем группировки и вынесения за скобки. В данном случае группировка приводит к формуле х1х4Vx3(х2Vx4), содержащей 5 символов переменных (ср. с реализациями (2.5) и (2.6), полученными в §2.2).

Как и в случае всюду определенных функций, для частичных функций от большого числа аргументов наиболее трудоемким является этап, связанный с отысканием наилучшего покрытия. Нахождение приближенного решения может быть осуществлено с использованием пошаговой процедуры, описанной выше для всюду определенных функций.

Сложность м.д.н.ф.

Рассмотрим вопрос о том, сколь сложными могут быть м. д. н. ф. функций от n аргументов (под сложностью д. н. ф. будем понимать число входящих в нее символов переменных).

Рассмотрим линейную функцию l_n (x₁, x₂, . . ., x_n) = x₁? x₂?…? x_n.

На соседних наборах (различающихся в одной компоненте) она принимает разные значения. Поэтому никакие два единичных набора этой функции не склеиваются, и ее м. д. н. ф. совпадает с с. д. н. ф. Функция l_n(x₁,x₂, ..,x_n) принимает 2^n-1 единичных значений (на всех наборах длины n с нечетным числом единиц), и каждому из них в с. д. н, ф. соответствует конъюнкция длины n.

Поэтому с. д. н. ф. (а следовательно, и м. д. н. ф.) этой функции содержит n2^n-1 символов переменных. Покажем, что м. д. н. ф. любой функции f(x₁, x₂,...,x_n) от n аргументов не сложнее, чем у l_n (x₁, x₂,...,x_n). Рассмотрим все единичные наборы функции f. Отбрасыванием последней компоненты образуем из них укороченные наборы длины n-1. Каждому укороченному набору (σ_1,….,σ_n-1) следующим образом сопоставим конъюнкцию. Если функция f имеет единственный единичный набор (σ_1,….,σ_n-1,σ_n) , совпадающий с укороченным в первых n-1 компонентах, то в качестве конъюнкции возьмем x^σ1_1…x^σn_in, а если таких единичных наборов два, то возьмем x^σ1_1…x^σn-1_in-1. Дизъюнкции всех полученных конъюнкций совпадает с f, ибо каждый единичный набор (σ_1,….,σ_n-1,σ_n), не имеющий соседнего по последней компоненте, реализуется индивидуально конъюнкцией x^σ1_1…x^σn_in, а всякая пара соседних наборов (σ_1,….,σ_n-1,σ_n,0) и (σ_1,….,σ_n-1,σ_n,1)-укороченной конъюнкцией x^σ1_1…x^σn-1_in-1. Число конъюнкций в полученной д.н.ф. совпадает с числом укороченных наборов и не превосходит 2^n-1 (общего числа наборов длины n-1). Поэтому сложность этой д.н.ф. (а следовательно, и м. д. н. ф.) не выше n2^n-1. Из процесса доказательства нетрудно заключить, что м. д. н. ф. максимальной сложности n2^n-1 имеют лишь две линейные функции от n аргументов:

l_n (x₁, x₂, . . ., x_n) = x₁? x₂?…? x_n.

Определение 1. Дизъюнктивная нормальная форма называется минимальной (сокращенно МДНФ), если она имеет наименьшую длину среди всех равносильных ей ДНФ.

Определение 2. Элементарная конъюнкция вида

, (1)

где ии для всехs, называется импликантой функции , если она входит в какую-нибудь ДНФ, представляющую функцию

Заметим, что последнее условие можно сформулировать иначе. Например, оно равносильно каждому из условий:

а)

б)

В общем случае, если

то говорят, что функция поглощается функцией , или поглощается.

Следовательно, можно сказать, что импликанта функции есть элементарная конъюнкция вида (1), которая поглощается функцией .

Определение 3.Импликанта функции называется простой, если никакая ее собственная часть не является импликантой функции .Импликанту функции ,вида

назовем совершенной.

Лемма 1.Пусть,- импликанты функции . Импликантапоглощает тогда и только тогда, когда является частью импликанты .

Пусть есть часть , т. е. = ’. Тогда по закону поглощения’, т. е.

. (2)

Обратно, пусть имеет место (2) и не есть часть. Тогдасодержит сомножитель , который не входит в. Возможны два случая:

а) не содержит переменного ;

б) содержит множитель .

Так как содержит , томожет принимать значение 1 лишь при . В то же время из условий “а” и “б” видно, что существует наборзначений переменных, в котором = и () = 1. Таким образом,= 1, а= 0, что противоречит условию (2).

Значение простых импликант объясняется следующим утверждением.

Теорема 1.Всякая импликанта функции содержащаяся в какой-либо МДНФ функции, является простой.

В самом деле, пусть

…(3)

есть любая МДНФ функции , где, …,- импликанты. Допустим, что импликантане простая. Тогда найдется ее собственная часть, которая является импликантой функции , т. е.

f. (4)

Из леммы 1 следует, что

(5)

Из равенств (3)-(5) имеем:

= (.

Так как () < (), то (3) не есть МДНФ функции . Полученное противоречие доказывает теорему 1.

Таким образом, всякая МДНФ функции составляется из ее простых импликант.

Определение 4. Дизъюнкция всех простых импликант функции называется сокращенной ДНФ функции .

Так как каждая импликанта функции поглощается некоторой ее простой импликантой, то сокращенная ДНФ функцииfпредставляет функцию .

Определение 5.ДНФ

функции fназывается тупиковой если- простые импликанты и

при любом .

Из всего сказанного виден путь нахождения МДНФ функции сначала находим сокращенную ДНФ, затем все тупиковые ДНФ. Тупиковые ДНФ наименьшей длины и будут минимальными ДНФ.

Ниже будет показано, как найти сокращенную ДНФ и все тупиковые ДНФ функции.

Заметим, что при небольших значениях n(например, приn= 2, 3, 4, 5) МДНФ функцииможно находить из следующих наглядных соображений.

Назовем множество

: 1}

n-мерным единичным кубом, а каждый набор () – вершиной этого куба. Каждой функцииf() сопоставим множество

N

В частности, множество сопоставленное элементарной конъюнкции

где при ,назовем гранью размерности или ранга . Ясно, что грань состоит из всех наборов значений переменных , в которых а значения остальных переменных произвольны: .

Для любых функций очевидны следующие соотношения:

1)

2)

3)

4)

5)

Из пункта 1-3 легко следуют утверждения 4 и 5. Из этого всего видно, что задача нахождения МДНФ функции эквивалентна нахождению такого представления множества объединением граней, в котором сумма рангов граней минимальна.

При этом роль простых импликант играют максимальные грани, т. е. грани, входящие во множество , которые не входят в грани больших размерностей, содержащиеся в. Таким образом, для нахождения искомого представления множествагранями нужно сначала найти все максимальные грани, а затем удалять из них грани, содержащиеся в объединении остальных. Из получающихся таким образом “неприводимых” представлений множествамаксимальными гранями следует выбрать искомое (самое экономное) представление.

Пример. Найти сокращенную и минимальную ДНФ функции

Изобразим геометрически трехмерный куб, подписывая около каждой его вершины ее координаты (см. рис. 1).

РИСУНОК 1.

Отметим на кубе вершины, содержащиеся в 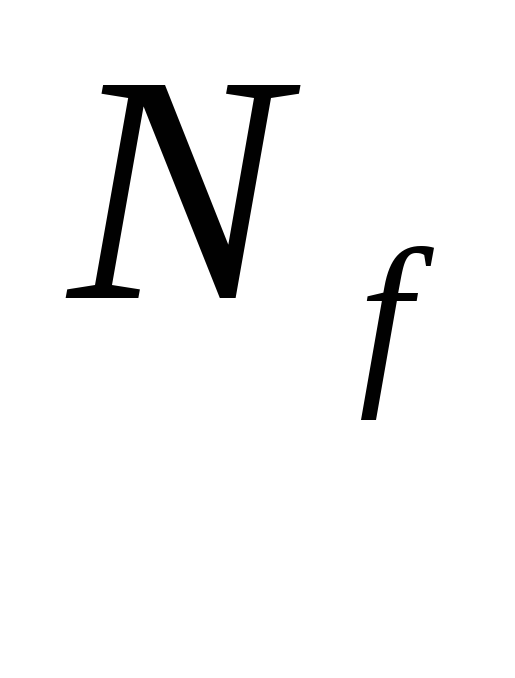, и найдем максимальные грани в. Из чертежа видно, что ввходят лишь грани размерности 0, т. е. точкии грани размерности 1, т. е. ребраЗначит, максимальными являются 6 граней размерности 1. Им соответствуют простые импликанты функцииЗначит,

есть сокращенная ДНФ функции . Из чертежа видно также, что множествосодержится в объединении лишь трех граней или Отсюда имеем две МДНФ