14. Методы построения простых импликантов.

Геометрическая интерпретация. Множество всех двоичных наборов будем рассматривать как множество вершинn-мерного единичного куба (на рис. 2.10 приведен трехмерный куб). Тогда всякая функция может быть описана множеством вершин куба, на которых она принимает значение 1. Рис. 2.10 соответствует функции , обращающейся в 1 на наборах (0,0,0), (0,0,1), (1,0,0), (1,0,1) и (1,1,1) (она задается табл. 1.1).

Функция является импликантом для , если соответствующее ей множество вер шин куба содержится в множестве вершин дляf. Всякая конъюнкция задает подкуб, представляющий собой множество вершин , для кото- рых, а значения остальныхn - k компонент могут быть выбраны произвольно. Подкуб, соответствующий конъюнкции длиныk, содержит вершин. В частности, подкуб для конъюнкции длиныn вырождается в вершину. На рис. 2.10 заштрихован подкуб, соответствующий конъюнкции (он представляет собой грань = 0).

Простой импликант определяет под куб, все вершины которого принадлежат множеству единичных вершин функции, и такой, что он не содержится ни в каком большем подкубе, обладающем этим свойством. Такие подкубы будем называть максимальными. Всякая д. н. ф. задает некоторое покрытие множества единичных вершин функции подкубами, соответствующими ее конъюнкциям.

На этом языке теорема 2.1 становится очевидной. Она означает, что в покрытии, соответствующем м. д. н. ф., используются только максимальные подкубы (максимальные подкубы покрывают большее число вершин в сравнении с содержащимися в них немаксимальными подкубами и имеют «меньшую стоимость», ибо задаются конъюнкциями меньшей длины). Из рассмотрения рис. 2.10 видно, что изображенная на нем функция имеет единственную м. д. н., ф. , соответствующую покрытию подкубами, один из которых представляет собой грань , а другой — ребро ,. В общем случае функция может иметь несколько м. д. н. ф. Кратчайшей д.н.ф. соответствует покрытие наименьшим числом подкубов. Ясно, что при построении такого покрытия можно использовать лишь максимальные подкубы.

Первым этапом в нахождении м. д. н. ф. (и кратчайшей д. н. ф.) является построение системы всех простых импликантов.

2.3.4. Построение простых импликантов. Рассмотрим некоторый импликант функции , являющийся конъюнкцией. Для удобства будем считать, что в него входят первыер переменных, т. е. что импликант имеет вид . На всех наборах () (при разных ) импликант равен 1. Поэтому функцияf на этих наборах также обращается в 1 и в ее с. д. н. ф. присутствуют всевозможные конъюнкции вида . Осуществив склеивания по переменной :

,

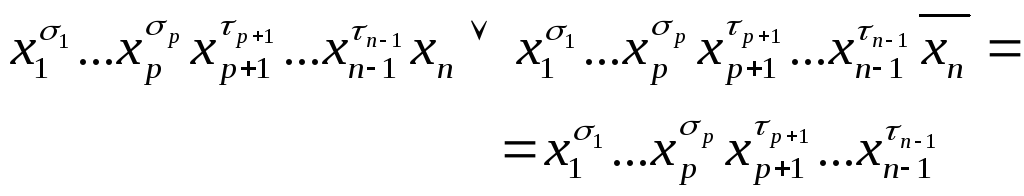из них можно получить всевозможные конъюнкции вида . Затем, произведя склеивания по переменной , придем к всевозможным конъюнкциям и т. д., пока не получим . Таким образом, всякий импликант, имеющий вид коньюнкции, можно получить из конъюнкций с. д. н. ф., последовательным применением операции склеивания. Легко видеть, что верно и обратное: всякая конъюнкция, полученная таким образой, является импликантомf. Отсюда можно сделать вывод, чтовсе импликанты, имеющие вид конъюнкций, и только они, могут быть образованы в результате последовательного склеивания конъюнкций из с. д. н. ф.

Рассмотрим пример. Пусть в с. д. н. ф. функции : входят конъюнкции , , , . Произведем последовательные склеивания по и по :

() ()=

==, в результате чего получим импликант . Конъюнкции удобно задавать наборами длиныnиз символов 0,1 и —. Если переменная входит в конъюнкцию в форме , то в этом наборе наi-м месте записывается , а если отсутствует, то наi-м месте проставляется —. Конъюнкции , например, соответствует набор 1 — 0 —. С использованием такого представления конъюнкций рассмотренный выше пример получения из с. д. н. ф. может быть описан следующим образом:

На основе сказанного приведем алгоритм построения всех импликантов, имеющих вид конъюнкции. Изложение будем сопровождать примером. Пусть функция задана таблицей 2.8.

Таблица 28

				f
0	0	0	0	1
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

Выпишем в полосе 1 таблицы 2.9 все наборы, на которых функция f обращается в 1. Для осуществления алгоритма их удобно выписывать разбитыми на группы

Таблица 2.9

0 0 0 0 +	0 0 0 - + 0 - 0 0 + - 0 0 0 +	- 0 0 - - - 0 0
		- 0 - 1 1 - 0 - I I I
0 0 0 1 + 0 1 0 0 + 1 0 0 0 +	0 0 - 1 + 0 1 - 0 - 0 0 1 + 1 0 0 - + - 1 0 0 + 1 - 0 0 +
0 0 1 1 + 0 1 1 0 + 1 0 0 1 + 1 1 0 0 +	- 0 1 1 + 1 0 - 1 + 1 - 0 1 + 1 1 0 - + I I
1 0 1 1 + 1 1 0 1 + I

В соответствии с числом единичных компонент в наборах. Поскольку склеиваются лишь наборы, отличающиеся в одной компоненте, то для того чтобы произвести все склеивания по одной переменной, достаточно просмотреть всевозможные нары наборов, входящих в соседние группы, результаты склеиваний наборов из полосы I поместим в полосе II. Наборы из полосы I, которые участвовали в склеиваниях, пометим значком + . В полосе II наборы уже автоматически разбиваются на группы по числу единиц (при склеивании наборов полосы I из групп с t-1 единицами и с i единицами получается набор полосы II с (-1 единицами). К образованным наборам снова применяем операцию склеивания (склеиваются пары наборов, которые содержат прочерк на одинаковых местах и различаются одной компонентой). При этом нужно опять просмотреть все пары наборов из соседних групп. Наборы, к которым применена операция, помечаем значком +. Результаты склеивания (соответствующие конъюнкциям длины 2) заносим в полосу III таблицы. В полосе III снова пытаемся осуществить склеивания, однако этого сделать не удается. На этом процедура завершается.

Вполученной таблице содержатся все импликанты функции f, имеющие вид конъюнкции. Простыми будут те из них, которые не помечены значком + (из них нельзя вычеркнуть ни одной переменной, иначе применима операция склеивания). В рассмотренном примере простыми импликантами являются конъюнкции x1x2x4, x2x3, x3x4, x2x4, x1x3 которые соответствуют наборам 01 - 0, -00-, --00, -0-1, 1-0 -.