Множества с операциями. 1

1. Определения: n-операция; бинарное отношение; алгебраическая система. 1

2. Булева алгебра, примеры (все подмножества множества, все делители числа m=p1p2…pn, pj – различные простые числа. 2

3. Изоморфизм алгебраических систем, пример изоморфизма группы R(.) - действительных чисел c операцией умножения с группой R(+) – действительных чисел с операцией сложения. 3

Алгебры высказываний и предикатов. 3

4. Операции над высказываниями, n-местный предикат, его связь с n-арным отношением. 3

5. Модель М() сигнатуры . Способы получения предикатов из предикатов. Квантор всеобщности. Квантор существования. 5

6. Термы. Формула на алгебраической системе М() (на предикатах). Свободные и связные переменные в формулах предикатов. 7

7. Формула над классом (множеством) логических функций. Примеры эквивалентных преобразований формул, в частности, правила поглощения, склеивания, вычеркивания. 8

8. Доказательство теоремы о разложении логической функции по К переменным. 12

9.Формула разложения по переменной. 13

10. Доказательство теоремы о представлении двоичной функции в виде СДНФ. 13

11. Представление в виде СКНФ. 15

12. Понятие ДНФ булевой функции. Импликанта логической функции. Простой импликант. 15

Строение м.д.н.ф. 15

16

13. Доказательство утверждения о том, что минимальная ДНФ (отличная от 0 и 1) является дизъюнкцией некоторых простых импликантов. 16

14. Методы построения простых импликантов. 17

15. Методы формирования МДНФ. 21

Формирование м. д. н. ф. 22

Для отыскания сокращенных и минимальных ДНФ функций от 4 переменных можно использовать проекцию 4-мерного куба, изображенную на рис. 2. 30

16. Доказательство теоремы о представлении двоичной функции в виде полинома Жегалкина. 39

Множества с операциями.

1. Определения: n-операция; бинарное отношение; алгебраическая система.

Определение 1.Операцией арности n,или n-арной операцией,на множествеМ прип> 0 называется произвольное отображение

f:MⁿM.

При этом образ элемента (а₁, ...,а_п) изМ при отображенииf называется результатом применения операции к элементама₁ ..., а_п изМ и обозначается в виде

f(a₁,...,a_n)

Результатом нуль-арной операции по определению считается некоторый фиксированный элемент множества М. В связи с этим нуль-арную операцию и обозначают, как правило, тем же символом, что и элемент множества М, являющийся значением этой операции.

Практически наиболее интересными являются бинарные операции. Если f-бинарная операция на множестве М, то вместо f(a₁,а₂) чаще пишут а₁fа₂. Во многих конкретных примерах вместо f используются символы +, •, -, о, U, и др.

Приведем примеры бинарных операций.

1. Бинарными операциями являются операции сложения и умножения на множествах N₀, Z, Q, R, С, а также операция вычитания на множествах Z , Q, R , С .

N-натуральные числа.Z-целые числа.Q-рациональные числа.R-действительные(вещественные ) числа.

2. Рассмотрим множество P(М) всех подмножеств фиксированного множества М. Так как пересечение и объединение любых двух подмножеств из M являются вполне определенными подмножествами из М, то операции пересечения и объединения пар подмножеств из М являются бинарными операциями на множестве P(М).

Заметим, что на P(М) обычно рассматривается еще унарная операция ' взятия дополнения: А' = М\А,

3. Пусть П(М) есть множество всех преобразований непустого мно-жества М. Следовательно, композиция преобразований есть бинарная операция на множестве П(M). То же самое можно сказать и о произведении преобразований множества М.

4. Обозначим через B(М) множество всех бинарных отношений на M. Определим для каждой пары отношений R₁ R₂ на М третье отношение R, положив для любых элементов a, b М aRb в том и только том случае, когда существует элемент сМ, такой, что aR₁с и cR₂b :

aRbсуществуетcM: aR₁c ,cR₂b

Отношение R называется произведением отношений R₁ R₂ и обозначается в виде R₁R₂. Произведение бинарных отношений есть бинарная операция на множестве B(М).

Определение 2. Бинарная операция * на множестве М называется коммутативной или ассоциативной, если для любых элементов а, b, с М выполняется соответственно равенство

ab=ba

(ab)c=a(bc).

Так, операции сложения и умножения чисел на N, Z, Q, R , С и бинарные операции, приведенные в примерах 2-3, коммутативны и ассоциативны. Так как на одном и том же множестве может быть задано несколь­ко бинарных операций, то могут существовать свойства, связывающие различные операции.

Определение 3. Пусть  и - две бинарные операции па множестве М. Операция * называется лево- или праводистрибутивной относительно операции , если для любых элементов а, b, с из М выполняется соответственно равенство

a(bс) = (ab) (ас),

(ab)c=(ac)(bc).

Если выполняются оба эти равенства, то говорят просто о дистрибутивности операции * относительно операции .

Определение 4. Множество М с заданными на нем операциями и отношениями называется алгебраической системой. При этом М называют основным множеством системы, а множество символов, используемых для обозначения определенных на M операций и отношений, - ее сигнатурой.

Алгебраическую систему с основным множеством М и с сигнатурой ={f₁, ..., f_k; R₁, ..., R_l}, состоящей из символов операций f_i арностей п_i и отношений R_j арностей т_i , обозначают в виде M(), или подробнее, М (f1,...,f_k R₁,..,R_l). При этом набор натуральных чисел <n₁,...,n_k;m₁,...m_k> называют типом системы M() Если на алгебраической системе определены только операции или только предикаты, то она называется соответственно алгеброй или моделью.

Примером алгебраической системы может служить множество на­туральных чисел N с бинарными операциями сложения и умножения и бинарными отношениями =, <. Примером модели является любое час­тично упорядоченное множество.

2. Булева алгебра, примеры (все подмножества множества, все делители числа m=p₁p₂…p_n, p_j – различные простые числа.

Определение 1. Булевой алгеброй называется множество В с двумя бинарными операциями -, V, одной унарной операцией и двумя нуль-арными операциями (т. е. выделенными элементами) 0 1, удовлетворяющими условиям {при любых а, b, c В):

1. (ab)c=a(bc),

2. (aVb)Vc=aV(bVc),

3.ab=bа,

4. aVb=bVa,

5. аа=a,

6. аVа = а,

7. а(а Vb)=a,

8. aV(ab) = а,

9. а(bVс) = (ab)V(аb),

10.aV(bc)=(aVb)(aVc),

11.aa=0,

12 aVa=1.

Элементы 0 и 1 булевой алгебры В называют соответственно ее ну-лем и единицей. Иногда их обозначают в виде 0_B и 1_B.

Примером булевой алгебры является множество всех подмножеств

произвольного множества М с бинарными операциями пересечения  и объединения , унарной операцией дополнения и нуль-арными операциями , М, играющими соответственно роль 0 и 1.

;Л Булеву алгебру образует также множество всех (положительных) делителей числа m, равного произведению различных простых чисел, с операциями

ab = н.о.д.(a, b),aVb = н..о.к. (а, b}, а' = m/a

и с числами 1 и т в роли нуль-арных операций соответственно 0 и 1.

3. Изоморфизм алгебраических систем, пример изоморфизма группы R(.) - действительных чисел c операцией умножения с группой R(+) – действительных чисел с операцией сложения.

Определение 1. Алгебраические системы А, В одной и той же сигнатуры ={f₁,..., f_k;R₁,...,R_l} типа <п₁,...,n_k; m₁,...,т_l> называются изоморфными, если существует биективное отображение :AB, такое, что:

1) для любой операции f_i и любых элементов а₁,...,а_niА вы- полняется равенство ¹

(f_i(a₁,...,a_ni))=f_i((a₁),...,(a_ni));

2) для любого отношения R_j и любых элементов a₁,..., а_mj

R_j(a₁,...,a_mi)Rj((a₁),...,(a_mi)).

При этом само отображение  называется изоморфизмом системы А на систему В.

Примеры алгебраических структур.

Опр:Бинарная операция на множестве Х – отображение декартового квадрата множества Х в себя:

Свойства операций:

1. Коммутативность .

2. Ассоциативность (*):

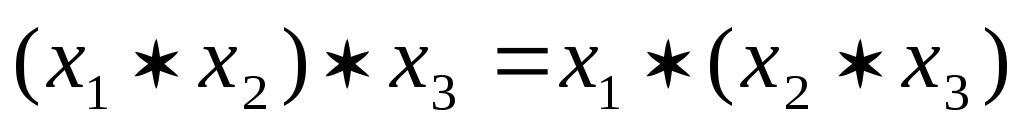
3. Дистрибутивность(*,0):

Группоид (G ,*) множество с одной операцией.

Полугруппа- группоид (G,*) с ассоциативной операцией *.

Группа – группоид (G ,*) , *- ассоциативна, нейтральный элемент е,ае=еа=а

для любого aG существует симметричный aG: aa=aa=e,

Кольцо (R,+,)

(R,+) – абелева группа

(R,) – полугруппа, операция  дистрибутивна относительно +.

Поле – коммутативное кольцо (ab=ba) c нейтральным элементом e относительно  , любой ненулевой элемент a обратим.