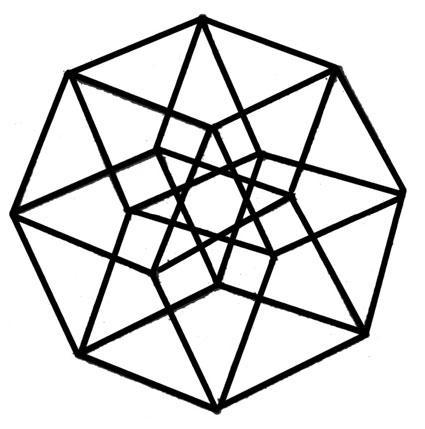
Для отыскания сокращенных и минимальных днф функций от 4 переменных можно использовать проекцию 4-мерного куба, изображенную на рис. 2.

РИСУНОК 2.

Теперь рассмотрим аналитические методы нахождения сокращенных, тупиковых и минимальных ДНФ.

А) Нахождение сокращенной ДНФ булевой функции по ее совершенной ДНФ.

Предварительно введем термины и обозначения. Условимся через обозначать элементарную конъюнкцию длины.

Элементарные конъюнкции

отличающиеся показателем лишь у одного переменного, называются соседними. Если в некоторой системе элементарных конъюнкций конъюнкция не имеет соседних, то она называется изолированной.

Очевидно, что

Будем говорить, что получена склеиванием конъюнкцийи, а,получены расклеиванием конъюнкции.

Теперь можно описать алгоритм нахождения сокращенной ДНФ функции

1)Для каждой элементарной конъюнкции совершенной ДНФ функции находим все соседние с ней конъюнкции, входящие в совершенную ДНФ.

2) К каждой паре соседних конъюнкций применяем операцию склеивания и из полученных таким образом элементарных конъюнкций длины n-1 выбираем множество всех попарно различных конъюнкций. В итоге получим:

где - изолированные элементарные конъюнкции, а- дизъюнкция всех полученных в пункте 2 элементарных конъюнкций длиныn-1.

Аналогично, применяя операции 1 и 2 к функции , получим:

Будем продолжать этот алгоритм до тех пор, пока не получим функцию в которой все элементарные конъюнкции изолированы.

Ниже будет доказана

Теорема 2.

(6)

есть сокращенная ДНФ функции .

Тот факт, что ДНФ (6) равна , очевиден. Остается показать, что она сокращенна, т. е., что множество входящих в нее элементарных конъюнкций совпадает с множеством всех простых импликант функции. Сначала дадим

Определение.Дизъюнктивную нормальную форму

назовем насыщенной, если

для любой элементарной конъюнкции , отличной от.

Примером насыщенной ДНФ может служить любая совершенная ДНФ. Она насыщена в силу своей единственности для каждой булевой функции.

Справедливость сформулированной выше теоремы легко следует из следующего утверждения.

Лемма. Пусть

(7)

насыщенная ДНФ; суть все ее изолированные конъюнкции и

(8)

дизъюнкция всех элементарных конъюнкций длины , полученных применением операций 1-2 к ДНФ (7). Тогда:

. ДНФ (8) – насыщенна;

. есть множество всех простых импликант длиныфункции;

. Множество простых импликант длины функциисовпадает с множеством простых импликант длиныфункции.

Доказательство. . Пусть- любая элементарная конъюнкция длиныи

.

Применяя к операцию расклеивания, мы получим пару соседних элементарных конъюнкцийи, которые содержатся в ДНФ (7) в силу ее насыщенности. Но тогда к ним должна была применяться операция склеивания и полученная при этом конъюнкциясодержится в (8). Это и означает, что ДНФ (8) насыщенная.

Так как ДНФ (7) насыщенная и ее элементарные конъюнкции, имеющие соседние конъюнкции, не могут быть простыми импликантами, то все простые импликанты длины функциисодержатся среди

Допустим, что некоторая из них, например , не является собственная часть конъюнкциипоглощается функцией. Тогда, очевидно, в качестве такой собственной части можно взять элементарную конъюнкциюдлины:простой импликантой функции. Это означает, что некоторая

и

А так как

и ДНФ (7) насыщенная, то содержится в (7). Следовательно в (7) элементарная конъюнкция имеет соседнюю, т. е. не является изолированной. Полученное противоречие и доказывает утверждение .

. В одну сторону очевидно. А именно, всякая простая импликанта длины функции является простой импликантой функции Докажем обратное.

Пусть - простая импликанта и не является таковой для . Это означает, что существует собственная часть , которая поглощается функцией . В качестве такой части можно выбрать элементарную конъюнкцию :

.

Так как для некоторого , не входящего в ,

и ДНФ (7) насыщенная, то все элементарные конъюнкции содержатся в (7), а поскольку они не являются в (7) изолированными, то Следовательно, не есть простая импликанта для , что противоречит выбору .

Пример. Найти сокращенную ДНФ для функции

Замечаем, что изолированных элементарных конъюнкций здесь нет. В результате склеивания всех пар соседних конъюнкций и приведения подобных, получим:

Здесь изолированными являются лишь конъюнкции

Применив операцию склеивания к соседним конъюнкциям, будем иметь:

В полученной функции все конъюнкции изолированные. По доказанной выше теореме

есть сокращенная ДНФ функции.

Б) Нахождение сокращенной ДНФ булевой функции по ее произвольной ДНФ.

В искомом алгоритме нахождение сокращенной ДНФ будет использоваться равносильность

для любых формул не содержащих . Эта равносильность непосредственно проверяется при и .

Пусть имеется представление булевой функции в виде дизъюнкции ее импликант:

(9)

1) Найдем в (9) импликанты вида

и такие, что в (9) нет импликанты равносильной конъюнкции . Тогда, заменив в (9) на получим новое представление функции в виде дизъюнкции импликант.

Теперь преобразование такого же типа применим к полученному представлению и т. д. до тех пор, пока не получим ДНФ, к которой не применимо преобразование типа 1.

2) К полученной ДНФ применим закон поглощения, заменяя дизъюнкции вида на до тех пор, пока это возможно.

В итоге получится сокращенная ДНФ булевой функции . Этот факт следует непосредственно из доказываемого ниже утверждения.

Теорема 3. Если к какой-либо ДНФ А булевой функции

применить всевозможные преобразования типа 1, то получится ДНФ В функции содержащая все простые импликанты .

Доказательство проведем индукцией по числу . При утверждение очевидно. Пусть и - простая импликанта ДНФ функции . Если ее длина , то присутствует в любой ДНФ функции , а потом и в В. Пусть , т. е. такое, что не содержит . Представим функцию в виде

,

где - функции не зависящие от . Так как - импликанта , то

.

Отсюда при и получим соответственно, что поглощается функциями , , а потом и функцией

Легко видеть, что - простая импликанта функции и В содержит ДНФ функции . Отсюда и из предложения индукции следует, что содержится в В. Теорема доказана.

Таким образом, с помощью преобразований типа 1 мы получим ДНФ, сожержащую все простые импликанты функции , а преобразованиями типа 2 избавимся от всех непростых импликант. В итоге получится сокращенная ДНФ функции .

В) Нахождение сокращенной ДНФ булевой функции по ее КНФ.

Пусть

(10)

представление функции в виде конъюнктивной нормальной формы.

1. Раскроем в (10) все скобки по правилу дистрибутивности конъюнкции относительно дизъюнкции, удалим из полученной формулы тождественно ложные конъюнкции, а остальные заменим на равносильные им импликанты функции . В итоге получим ДНФ функции :

(11)

2. Удалим из ДНФ (11) каждую элементарную конъюнкцию,

которая поглощается какой-либо другой конъюнкцией из (11).

В итоге получим сокращенную ДНФ функции , поскольку ДНФ (11) содержит все простые импликанты функции . Последний факт доказывается по той же схеме, что и теорема 3.

Г) Нахождение тупиковых и минимальных ДНФ булевой функции по сокращенной ДНФ.

По определению тупиковой ДНФ все ее импликанты простые и потому содержатся в сокращенной ДНФ. Отсюда следует, что для нахождения тупиковых ДНФ нужно уметь выяснять, поглощается ли в ДНФ произвольная элементарная конъюнкция дизъюнкцией остальных. Для решения последнего вопроса докажем критерий поглощения.

Лемма. Пусть ДНФ поглощает конъюнкцию и . Тогда поглощается ДНФ

Допустим, что это не так, т. е. Тогда для некоторого набора значений переменных А так как , то , а потому и Следовательно, , т.е. не поглощается ДНФ , что противоречит условию.

Функции и называются ортогональными, если . Доказанная лемма позволяет при исследовании на поглощение некоторой конъюнкции не принимать во внимание ортогональные к ней конъюнкции.

Теорема (критерий поглощения). Пусть некоторая ДНФ; - конъюнкция не ортогональная конъюнкция всех сомножителей, входящих в и , а - конъюнкция остальных сомножителе из ; при . ДНФ поглощает тогда и только тогда, когда

(12)

Доказательство. Пусть выполнено условие (12) и Тогда существует набор значений переменных , такой, что а потому и С другой стороны, по условию (12) а потому для некоторого . Пусть, например, Тогда и, следовательно, Получим противоречие.

Обратно, пусть и условие (12) не выполнено. Тогда для некоторого набора , . Так как то в не может входить отрицание какого-либо сомножителя из . Следовательно, в , а потому и в ДНФ входят лишь переменные, не входящие в . Пусть, например, в входят переменные а в Тогда

при любых значениях Так как не ортогональна , то а потому для некоторых имеем Таким образом, при :

что противоречит условию. При условие (12) тривиально.

Пример. Используя критерий поглощения, найти МДНФ для функции предыдущего примера.

Сокращенная ДНФ нашей функции имеет вид:

(13)

Выясним, какие из конъюнкций этой ДНФ не поглощаются дизъюнкцией остальных. Рассмотрим конъюнкцию Она не ортогональна лишь конъюнкциям которые не

поглощают ее, поскольку не выполняется условие (12):

Аналогично не поглощается остальными и Далее убеждаемся, что в (13) каждая из конъюнкций поглощается остальными и в ДНФ

каждая из конъюнкций поглощается остальными. Удаляя конъюнкции, поглощаемые остальными, получаем 4

ДНФ:

в этих ДНФ ни одна из конъюнкций не поглощается остальными, а потому это суть все тупиковые ДНФ функции . А так как они имеют одну и ту же длину, то все являются минимальными.

В заключение этого параграфа мы укажем еще один метод нахождения МДНФ из сокращенной ДНФ – метод Квайна. Рассмотрим его на предыдущем примере. Составим таблицу 1, у которой во входную строку входят все конъюнкции совершенной ДНФ функции , а во второй столбец – все конъюнкции из сокращенной ДНФ.

ТАБЛИЦА 1.

	1111	1110	1101	1100	1001	1000	0110	0011	0010	0000	0111
									+	+
	+	+	+	+
	+	+					+				+
			+	+	+	+
							+	+	+		+
						+				+

На пересечении строки с конъюнкцией , со столбцом с конъюнкцией ставим знак “+” в том и только том случае, когда поглощает , т. е. является частью . Далее, глядя на таблицу, мы должны выбрать из сокращенной ДНФ минимальное число конъюнкций, которые бы поглощали все конъюнкции совершенной ДНФ. В нашем случае мы замечаем, что конъюнкция поглощается только конъюнкцией . Значит, должна входить в любую тупиковую ДНФ функции . По тем же соображениям в любую тупиковую ДНФ входят . С другой стороны, из таблицы видно, что для поглощения

всех элементарных конъюнкций совершенной ДНФ функции нужно взять из сокращенной ДНФ конъюнкции , или или или , В итоге мы приходим к указанным выше четырем минимальным ДНФ функции .