-
Формулы Чебышева и Сомова-Малышева.
Степень подвижности плоского механизма (все звенья движутся в параллельных плоскостях) определяется по формуле П.Л. Чебышева
W = 3n - 2P5 – P4,
где n – число подвижных звеньев; P5 – число КП 5-го класса; P4 – число КП 4-го класса.
Степенью подвижности механизма называется число степеней свободы механизма относительно неподвижного звена (стойки).
Формула Сомова-Малышева для кинематической цепи общего вида:
W=6n–p1–2p2–3p3–4p4–5p5,
где n – число подвижных звеньев кинематической цепи. Данное уравнение носит название структурной формулы кинематической цепи общего вида.
-
Коэффициент полезного действия механизма.
КПД при последовательном соединении механизмов
В этом случае движение (и мощность) передается последовательно от одного механизма к другому. Полезной работой для предыдущего механизма является приведение в движение следующего. То есть полезная работа на выходе предыдущего механизма является одновременно движущей для последующего. Полезной работой всей системы является работа на выходе из последнего механизма системы:
Таким образом, общий коэффициент полезного действия системы последовательно соединенных механизмов равен произведению коэффициентов полезного действия этих механизмов:
Так как КПД любого механизма меньше единицы, то КПД системы последовательно соединенных механизмов оказывается всегда ниже худшего из механизмов этой системы. Поэтому, если применяется система последовательных механизмов (или отдельных элементов), то не следует включать в эту систему механизмы с низкими КПД.
Если последовательно соединяется «n» одинаковых механизмов:
|
То |
|
|
|
КПД при параллельном соединении механизмов
Несколько механизмов приводятся в движение одним двигателем. Полезная работа системы складывается из полезных работ на выходе из каждого механизма. На приведение в движение каждого из механизмов двигатель затрачивает часть своей энергии. Тогда коэффициент полезного действия такой системы можно представить следующим образом:
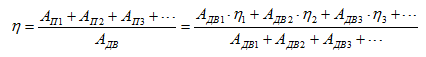
В данном случае величина общего КПД зависит от доли энергии, отдаваемой двигателем механизмам с более высокими или более низкими КПД. Но во всех случаях общий КПД занимает некоторое промежуточное значение по отношению к частным КПД механизмов, соединенных в систему (КПД системы будет тем выше, чем большая часть энергии двигателя будет отдаваться механизмам с высокими КПД).
Если параллельно соединяется «n» одинаковых механизмов:
Т.е. при параллельном соединении одинаковых механизмов КПД системы не изменяется и равен КПД одного механизма.
-
Уравнение движения механизма.
Для установления истинного закона движения уравнение энергетического баланса записывается в дифференциальной форме, которое в данном случае носит название уравнения движения машины.
Дальнейшее решение задачи осуществляется интегрированием уравнения движения машины:
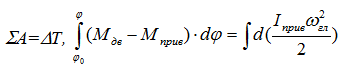
Из-за несоответствия характеристики двигателя и приведенного момента происходит отклонение истинного закона движения главного звена от первоначально заданного, происходят колебания угловой скорости.
Эти колебания оцениваются коэффициентом неравномерности хода. Коэффициент неравномерности хода определяется для цикла установившегося движения, обычно обозначается δ и определяется следующей формулой:
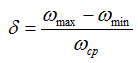
Опыт эксплуатации машин показывает, что на качество работы машины в большей степени влияет величина колебаний скорости главного звена, а не закон, по которому эти колебания происходят.
Поэтому решение задачи обычно сводится к определению коэффициента неравномерности хода δ, после чего он сравнивается с допустимой величиной [δ] для данного типа машин. Решение уравнения движения машины (интегрирование) и определение коэффициента неравномерности хода обычно производят графическими методами.
Если коэффициент неравномерности хода окажется больше допустимого для данного типа машин, то необходимо отрегулировать ход машины, т.к. колебания скорости вызывают дополнительные динамические нагрузки на детали машин, а также ухудшают рабочий процесс машины. Простейшим способом регулирования хода машины является постановка маховика.