
- •Вопросы по дисциплине "Теория механизмов и машин"
- •Кинематическое исследование кривошипно-коромыслового механизма методом планов.
- •Законы движения толкателя кулачкового механизма.
- •Назначение и задачи, решаемые кинетостатикой механизма.
- •Классификация действующих сил в механизмах.
- •Построение теоретического и рабочего профиля кулачка.
- •Приведение сил и масс.
- •Формулы Чебышева и Сомова-Малышева.
- •Коэффициент полезного действия механизма.
- •Уравнение движения механизма.
- •Строение механизма. Группы Ассура.
- •Углы давления и передачи в кулачковых механизмах.
- •Кинематический анализ кривошипно-шатунного механизма методом планов.
- •Трение в кинематических парах.
- •Назначение и классификация кулачковых механизмов.
- •Цилиндрическая эвольвентная зубчатая передача.
- •Кинетическая энергия и работа сил, действующих в машинах.
- •Аналоги скоростей и ускорения.
- •Синтез планетарных передач.
- •Свойства эвольвентного зацепления.
- •Проектирование кулачка по кинематическим параметрам.
- •Методы изготовления зубчатых колёс.
- •Графическое интегрирование и дифференцирование.
- •Неравномерность движения машины при установившемся режиме.
- •Назначение и проектирование маховика.
- •Определение передаточных отношений зубчатых механизмов.
- •Кинематика кулисного механизма.
- •Основная теорема зацепления.
- •Качественные показатели зубчатых передач.
- •Аналитический метод кинематического исследования механизмов.
- •Минимальное число зубчатого колеса.
- •Динамическая модель машины.
- •Диаграмма Виттенбауэра.
- •Метод обращённого движения.
- •Масштабные коэффициенты в методе диаграмм.
- •Динамический синтез кулачковых механизмов.
- •Подбор чисел зубьев планетарного механизма.
- •Скольжение в зубчатом зацеплении.
- •Явление подрезания зубьев.
- •Связь тмм с другими науками.
-
Определение передаточных отношений зубчатых механизмов.
Передаточное число зубчатой передачи определяется по формуле:
![]()
где ![]() и
и ![]() -
числа зубьев колес 1 и 2, соответственно.
-
числа зубьев колес 1 и 2, соответственно.
Знак «+» берется для внешнего зацепления (рис.1 и рис.2), знак «–» для внутреннего зацепления. Виды зацеплений приведены на рис.2. Знаки учитываются только для зубчатых передач с параллельными осями вращения колес.
Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней.
![]()
Передаточное число планетарного механизма определяется по формуле:
![]()
где ![]() -
передаточные числа ступеней (с учетом
знаков) при остановленном водиле.
-
передаточные числа ступеней (с учетом
знаков) при остановленном водиле.
-
Кинематика кулисного механизма.
Выбираем
масштаб:
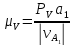
Скорость
точки
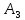 :
:
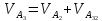
Относительная
скорость звеньев 3 и 2:
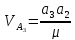
Модули
абсолютной скорости точки
 цилиндра:
цилиндра:
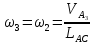
-
Основная теорема зацепления.
Общая нормаль к профилям зубчатых колес, находящимся в зацеплении, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям, т.е.,
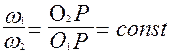
где О1, О2 – центры вращения соответственно шестерни и зубчатого колеса; Р – полюс зацепления.
Для
доказательства основной теоремы
рассмотрим зацепление двух зубьев в
некоторый момент времени в точке М со
скоростями этих точек
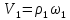 и
и
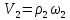 .
Проведем через точку касания М общие
касательную ТТ и нормаль nn.
Очевидно,
что условием непрерывности зацепления
при вращении колес будет равенство
проекций скоростей на общую нормаль
.
Проведем через точку касания М общие
касательную ТТ и нормаль nn.
Очевидно,
что условием непрерывности зацепления
при вращении колес будет равенство
проекций скоростей на общую нормаль
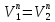 .
Обозначая углы векторов с нормалью
через
.
Обозначая углы векторов с нормалью
через
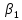 и
и
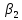 имеем
имеем
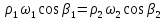 ,
,
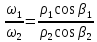
-
Качественные показатели зубчатых передач.
Коэффициент
перекрытия учитывает
непрерывность и плавность зацепления
в передаче. Такие качества передачи
обеспечиваются перекрытием работы
одной пары зубьев работой другой
пары. Для этого каждая последующая пара
зубьев должна войти в зацепление еще
до того, как предшествующая пара выйдет
из зацепления. О величине перекрытия
судят по коэффициенту перекрытия,
который выражают отношением угла
торцового перекрытия к угловому шагу.
Угол торцового перекрытия
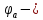 это угол поворота колеса от положения
зубьев при входе в зацепление, когда
они касаются в точке
В’,
до положения зубьев при выходе из
зацепления, когда они касаются в точке
B''.
Следовательно, коэффициент перекрытия
прямозубой передачи
это угол поворота колеса от положения
зубьев при входе в зацепление, когда
они касаются в точке
В’,
до положения зубьев при выходе из
зацепления, когда они касаются в точке
B''.
Следовательно, коэффициент перекрытия
прямозубой передачи
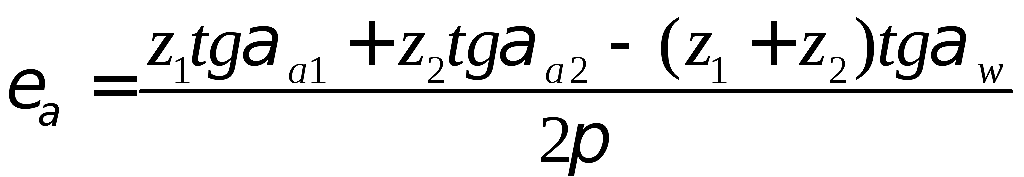
Коэффициент скольжения учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе зацепления. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей. Коэффициенты скольжения выражаются формулами:
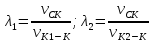
где 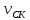 -
скорость скольжения;
-
скорость скольжения;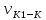 и
и
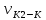 - скорости перемещения точек контакта
по профилям зубьев первого и второго
колеса.
- скорости перемещения точек контакта
по профилям зубьев первого и второго
колеса.
Коэффициент удельного давления учитывает влияние геометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев. При чрезмерном нагружении контактные напряжения могут быть столь значительны, что вызовут выкрашивание материала на рабочей поверхности зубьев.
Контактные напряжения определяются по формуле Герца:
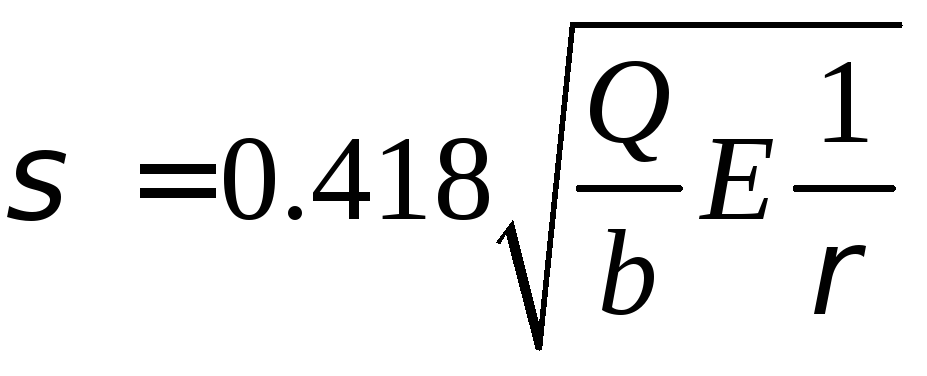
где Q- сила взаимодействия зубьев; b- ширина зубчатых колес;
E = 2E1E2/( E1 + E2)- приведенный модуль упругости их материалов; ρ- приведенный радиус кривизны эвольвентных профилей в точке контакта, посредством которою определяется влияние геометрии зуба на контактные напряжения.
Для
текущего момента зацепления зубьев:
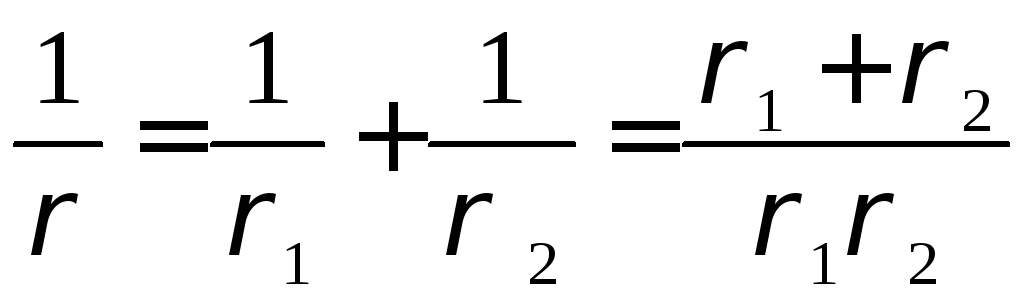
или,
согласно свойствам эвольвентных
профилей:
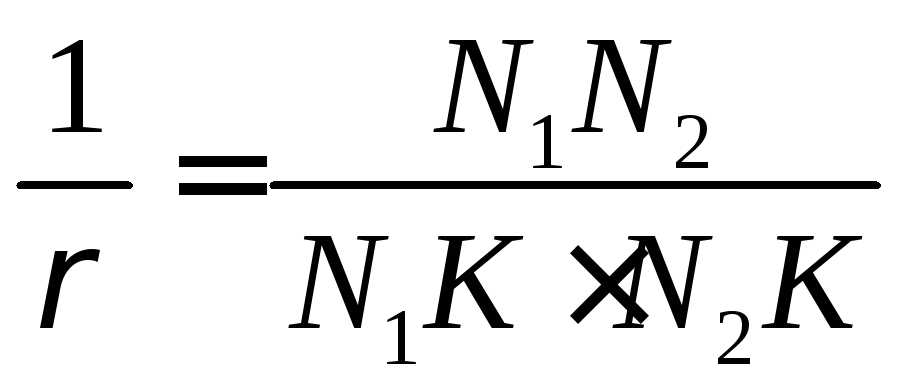
Коэффициентом удельного давления u называется отношение:
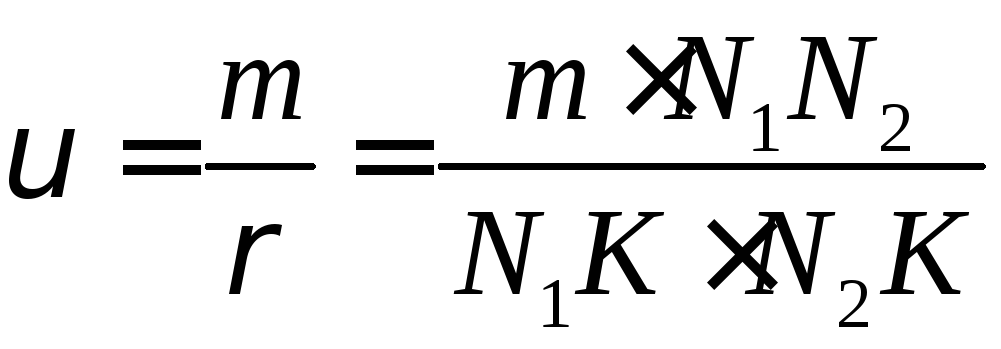
Коэффициент u - величина безразмерная, не зависящая от модуля m, так какпропорционален модулю.
