Лекции / Курс лекций 4

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

Глава 4. Теория интеграла

Далее всюду в этой главе, если не оговорено противное, рассматриваются однозначные функции.

§1. Понятие интеграла. Теорема Коши.

1.Интеграл и его свойства. Для кривой  и функции f(z), определенной на ней, рассматриваются интегральные суммы , см. рис.

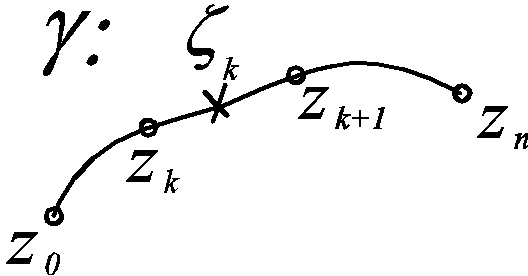
Интеграл определяется, как предел этих сумм в стандартном смысле и обозначается . Если кривая имеет параметризацию z(t), t[,], интегральные суммы в определении будут выглядеть следующим образом

.

Для непрерывной функции f(z) и непрерывно дифференцируемой кривой z(t), t[,] эти суммы будут сходиться к интегралу . Расписывая действительную и мнимую части этот интеграл можно выразить через криволинейные интегралы

.

Это равенство можно принять за определение интеграла в частном случае, когда и последние два интеграла существуют.

Свойства

1) Линейность

2) Аддитивность по множеству

3)

4) , из определения.

5) Если  - кусочно гладкая и f_k() сходится равномерно на  к f(), то следует из 4.

6) Определение интеграла по D=₀₁…_m.

2.Теорема Коши.

Если D- ограниченная область, D, граница которой  - кусочно гладкая Жорданова кривая из D, гомотопная нулю (область, ограниченная этой кривой, односвязна ) и f аналитическая в D, то .

Доказательство. Для представления интеграла воспользуемся формулой Грина

Формула Грина справедлива и для многосвязных областей. Поэтому справедлива

Обобщенная теорема Коши. Пусть D- ограниченная область с границей D=₀₁…_m, f аналитическая в D и непрерывная в , тогда .

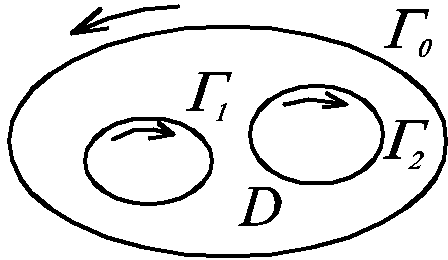
Следствие. В области D интеграл не зависит от пути интегрирования, а только от начальной и конечной точек кривой.

Таким образом, интеграл от аналитической функции в многосвязной области D не изменяется, если путь интегрирования непрерывно деформировать, оставляя неподвижными концы.

§2 Интеграл Коши

1.Интегральная формула Коши.

Пусть D- m- связная область с границей D=₀₁…_m-1 и f – аналитическая в D, непрерывная в функция. Имеет место формула

Доказательство. Если zDD, то равенство нулю интеграла следует из аналитичности подинтегральной функции для D. Пусть C – окружность с центром в z: (t)=z+re^it достаточно малого радиуса. В этом случае, согласно обобщенной теореме Коши, откуда следует, что . Так как d=r i e^it dt, то. Далее стягиваем С к нулю и используем теорему о среднем. Отметим, что , то есть последний интеграл является константой.

Следствие. Теорема о среднем. Если f непрерывна в |z|r и аналитическая в |z|<r, то

2.Интеграл типа Коши. Интегралом типа Коши называется интеграл

, где  - кусочно-гладкая замкнутая кривая Жордана, ограничивающая односвязную область D, а -непрерывная на  функция.

Теорема. Интеграл типа Коши является аналитической функцией в области D и

Доказательство.(только аналитичность, существование старших производных и формула для их вычисления будет доказана позже в разделе формулы Тейлора).

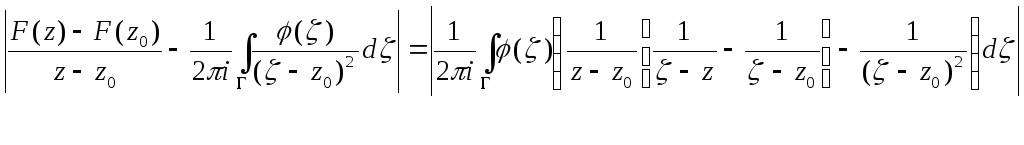
Выберем  окрестность точки z₀ , целиком лежащую в области D

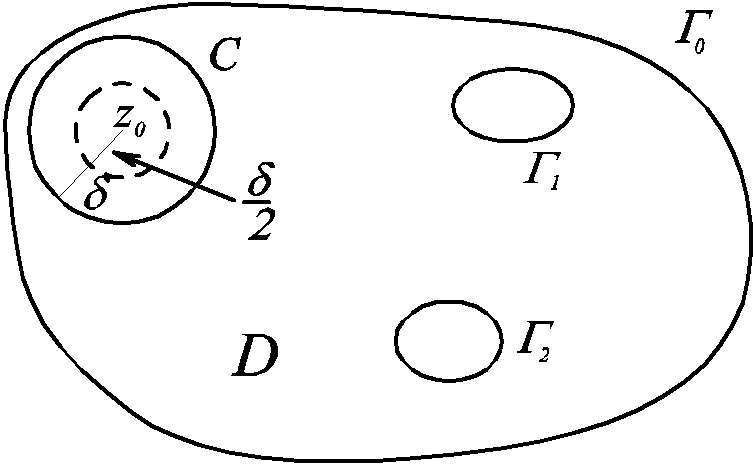
Если |z-z₀|</2, то расстояние от  до таких точек z будет больше чем /2, тогда , откуда следует неравенство

Переходя к пределу, получим требуемое равенство.

Следствие. Аналитическая в D функция имеет там производные любого порядка (доказательство в разделе формулы Тейлора).

§3 Первообразная.

1.Теорема Морера.

Теорема. Пусть D односвязная область, f() непрерывна в D и интеграл , z,z₀D не зависит от пути интегрирования, или, что тоже для любой замкнутой кривой Жордана, лежащей в D. Тогда F(z) аналитическая в D и F(z)=f(z).

Доказательство. Рассмотрим две точки z и z+z, путь из z₀ в z обозначим , путь из z₀ в z+z пусть будет ₁, где ₁:z(t)=z+z t, t[0,1].

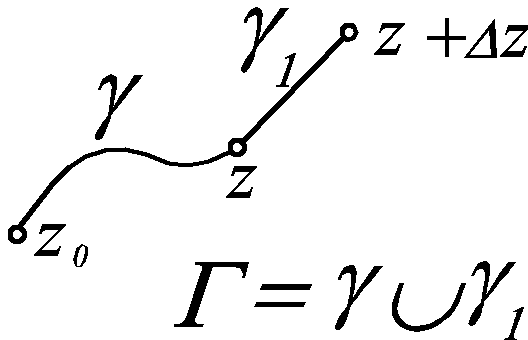
Тогда

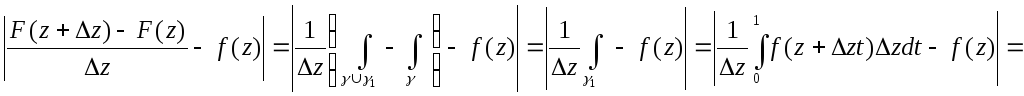
, при z0.

Определение. Функция F(z) такая, что F(z)=f(z) называется первообразной для f(z) на рассматриваемой области.

Теорема. Любые две первообразные одной и той же функции отличаются на константу.

Доказательство. Пусть F₁(z), F₂(z) первообразные для f(z). Положим =F₂ - F₁. Так как  голоморфна, то , кроме того, из условия , поэтому ,откуда и следует требуемое утверждение.

Напоминание. (z)= (x,y)= ,_x=u_x+iv_x, _y=u_y+iv_y

2.Формула Ньютона-Лейбница

Теорема. Если F(z) первообразная аналитической функции f(z), то

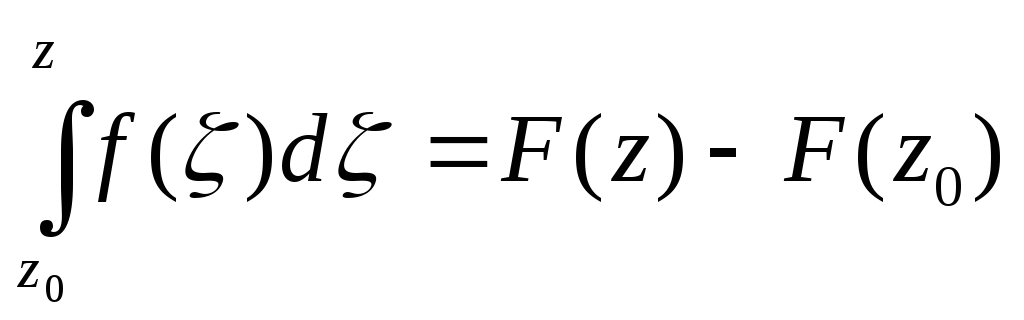
в частности .

Доказательство. Если F(z) – первообразная, то

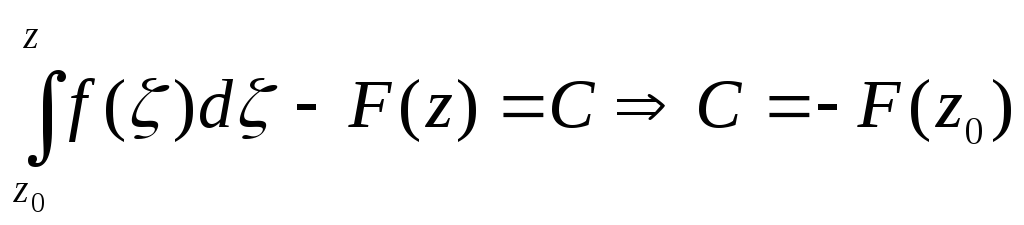
ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru