Лекции / Курс лекций 7

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

Глава 7. Преобразование Лапласа.

Введение. Интегралы, зависящие от параметра.

Пусть С – кусочно гладкая, не ограниченная в одну сторону, кривая

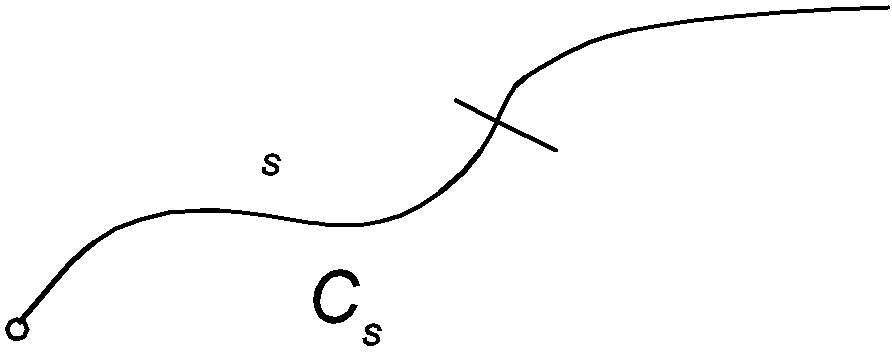
Пусть f(z,) определена при zD ( некоторая область ) и С. Интеграл от параметра определяется по формуле

Этот интеграл называется сходящимся равномерно в D, если

Признак Вейерштрасса. Если

1. для С,zD : |f(z,)| g() , g() действительно-значная функция,

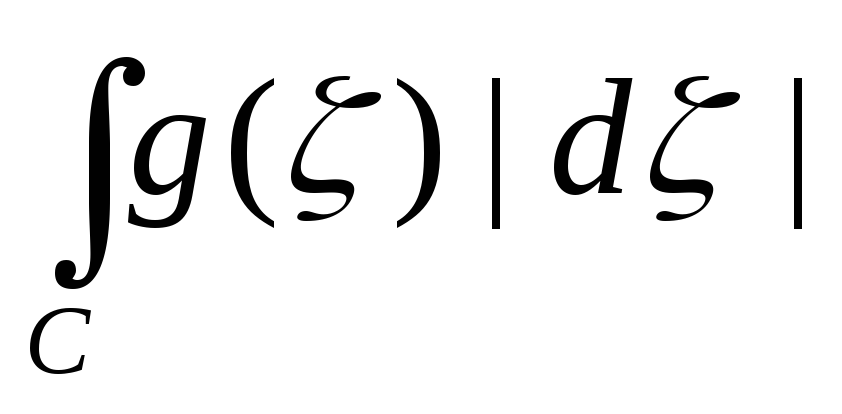2. сходится,

то сходится равномерно на D.

§1 Преобразование Лапласа.

Определение. Комплекснозначная функция f(t), t(-,) называется оригиналом, если

1. f(t)=0 при t<0

2. в (a,b) есть лишь конечное число разрывов первого рода. Иногда, дополнительно будет требоваться выполнение условия Липшица

|f(t+h) - f(t)|  A|h|^, для всех h,|h| h₀, 1 на интервалах непрерывности функции

3. M s t: |f(t)| Me^st (*)

Число , S – множество тех s, для которых выполнено условие (*), называется показателем роста оригинала.

Пример. Функция Хевисайда

Изображением функции оригинала f(t) ( по Лапласу ) называют функцию комплексного переменного p=s+i, определяемую равенством

Пишут F=L[f], F  f, f  F.

Замечание. Отметим, что если f(t) оригинал, то и t^kf(t) – также оригинал. Кроме того, интеграл будет сходиться равномерно по параметру в любом множестве Re p  q > s₀ .

Это следует из признака Вейерштрасса с учетом неравенств

|t^k f(t)e^-pt| Me^te^ste^{-(Re p)t} Me^te^ste^{-q t} M =Me^{- t},>0, где  выбрано так, что |t^k | Сe^t. Кроме того, | f(t)| B e^st , s+ < q.

Теорема 1. Для любого оригинала f(t) с показателем s₀ , изображение F(p) определено в полуплоскости s=Re p > s₀ , является в этой области аналитической функцией, стремящейся к 0 при s ( равномерно относительно arg p ). При этом

Доказательство.

Сходимость интегралов и следует из сделанного замечания. Обозначим , . Интегралы, полученные формальным дифференцированием

,

,

сходятся равномерно на любых отрезках изменения параметров (по параметру x отрезок, где имеет место равномерная сходимость должен лежать в области x > s₀), поэтому исходные интегралы можно дифференцировать по параметру и выполнены условия Коши Римана. Далее при s = Re p > s₁ > s₀

Следствие.

Теорема 2. Если Ff (f – кусочно гладкая ), то в точках непрерывности f(t) имеет место равенство

, где интеграл берётся вдоль любой прямой Re p = const > s₀, и интеграл берётся в смысле главного значения

без доказательства.

Теорема 3 ( Достаточные условия существования оригинала ). Если F(p) аналитична в { Re p > s₀ } и при p, тогда интеграл

не зависит от a, является оригиналом и F(p)=L[f].

( только формулировка )

§2 Свойства преобразования Лапласа

В этом параграфе везде под f(t) понимается f(t)H(t) (H - функция Хевисайда ).

Отметим, что

1. Линейность.

f(t)+g(t)F(p)+G(p)

2) Свойство подобия. При 0

3) Свойство запаздывания.

Для  f(t-)e^-pF(p). Действительно

4. Как уже отмечалось, F⁽ⁿ⁾(p)(-1)ⁿtⁿf(t), откуда следует

5. Дифференцирование оригинала

f(t)pF(p)-f(0),

действительно

Следствие. f⁽ⁿ⁾(t)pⁿF(p)-p^n-1f(0)-p^n-2f(0)-…-f^(n-1)(0)

Доказательство. F[f]=pF[f]-f(0),F[f]=pF[f]-f(0)=p(pF[f]-f(0))-f(0)

6. Интегрирование изображения

Если f(t)F(p), Re p > s₀ и - оригинал, то

Доказательство.

7. Интегрирование оригинала.

Если f(t)F(p), Re p > s₀, то

Доказательство. f(t)=g’(t)pG(p)-g(0)=pG(p) откуда F(p)=pG(p)

8. Свертка оригиналов и умножение изображений.

Определение.

Отметим, что f*g=g*f, Сделать замену u = t - , d = -dt.

f*gF(p)G(p)

Отметим, что если f, g – оригиналы, то и f*g – оригинал.

9. Умножение оригиналов, свёртка изображений

без доказательства.

10. Свойство смещения

F(p-)e^tf(t)

Доказательство из определения.

11. Первая теорема разложения (Теорема 1 Хевисайда).

Если F(p) аналитична в {R<|p|<} и

то оригиналом является

Доказательство.  - устранимая о.т.  |F(p)|<M,|p|R.Положим , аналитична в круге |q|<1/R, поэтому неравенство Коши даёт для коэффициентов |c_-k|<MR^k. Таким образом,

.

Таким образом, исходный ряд мажорируется сходящимся степенным рядом в любом круге. В этом случае ряд можно почленно интегрировать

по свойству 4) при r

, поэтому

12. Вторая теорема Хевисайда. Если

    1. F(p) мероморфна в некоторой полуплоскости Re p > s₀ и F()=0

    2. 

    3. F(p)0 при p равномерно относительно arg p

Тогда оригиналом для F служит ( умноженная на H(t) ) функция

по полюсам в порядке убывания их модулей функции F.

Доказательство. При сделанных предположениях для оригинала f(t)F(p) справедлива формула

(*)

Обозначим через C’_n часть окружности C_n, расположенную слева от прямой Re p = a, через aib_n точки пересечения C_n с этой прямой и через _n контур, составленный из [a-ib,a_ib] и C’_n, проходимый против часовой стрелки.

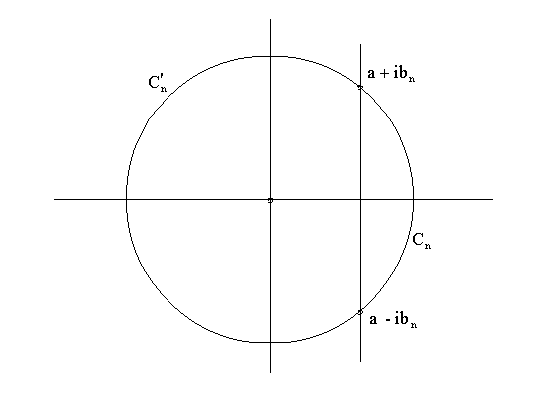
Так как по лемме Жордана при t < 0

то при t>0 вместо (*) можно писать

ч.т.д.

Следствие. Если функция дробно-рациональная и дробь правильная, то оригиналом ее служит функция

где p_k

полюсы F(p), n_k – из кратности, сумма берется по всем полюсам.

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru