Лекции / Курс лекций 5

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

Глава 5. Ряды Тейлора и Лорана

§1 Ряд Тейлора аналитической функции

Напоминание. Равномерно сходящийся на g ряд из непрерывных функций можно почленно интегрировать.

1.Теорема Тейлора.

Теорема. Если f аналитическая функция в области D, то для каждой точки z₀ÎD имеет место разложение

разложение единственно.

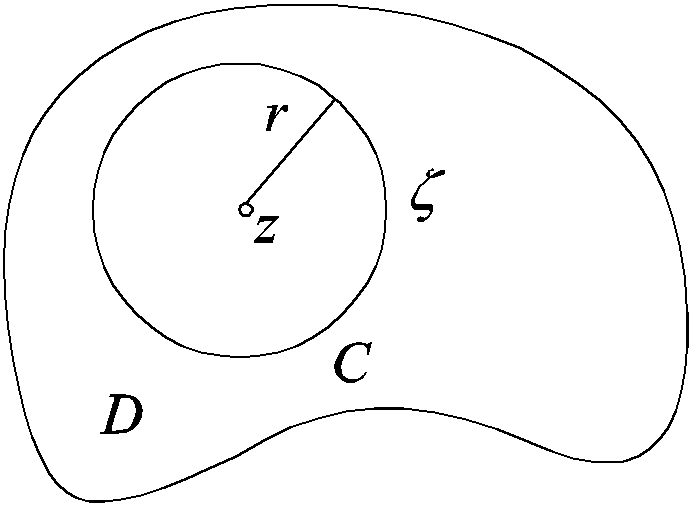
Доказательство. Пусть d меньше, чем расстояние от z₀ до границы ¶D.

Из аналитичности f(z) следует, что для окружности C с центром z₀ и радиуса d получим ( |z-z₀|< d )

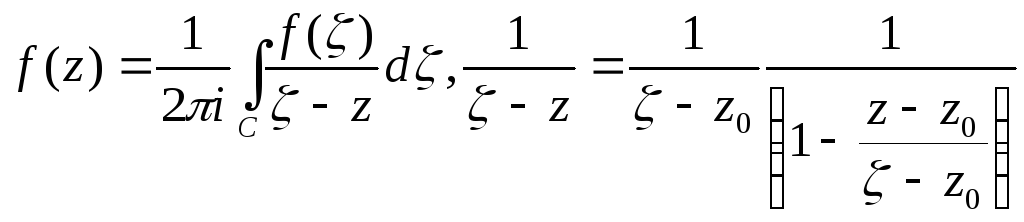
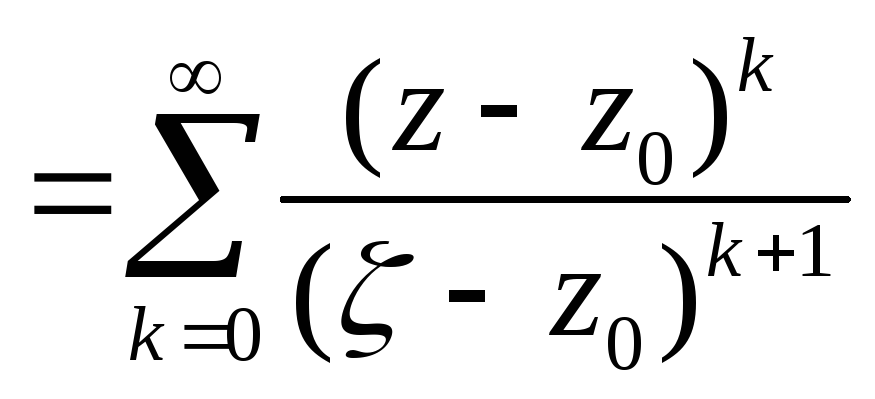. Таким образом

=

из Сл.2 теоремы пункта 1 главы 2 следует, что

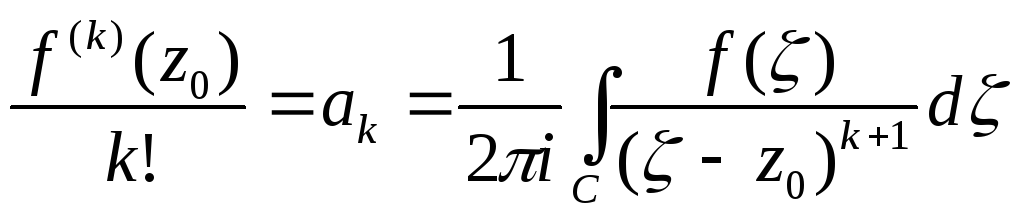. Единственность следует из той же теоремы.

Равномерная сходимость ( для интегрирования ) следует из неравенства.

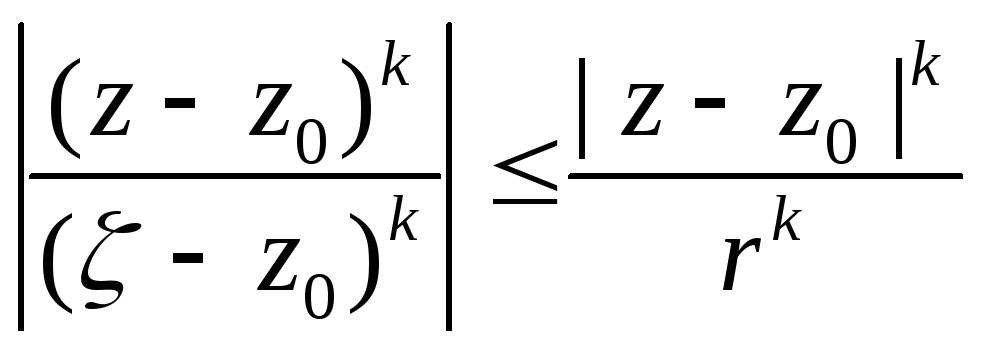
2.Неравенство Коши для коэффициентов ряда Тейлора. Теорема Лиувиля.

Утверждение. Если аналитическая в |z-z₀|<R функция f(z) ограничена на окружности |z-z₀|=R, |f(z)|M, то для коэффициентов a_k в разложении

справедливы неравенства

Доказательство. ч.т.д.

Теорема Лиувиля. Если f аналитическая во всей плоскости С и ограничена, то она константа.

Доказательство. Берём R.

§2 Единственность аналитической функции. Принцип максимума модуля.

1.Внутренняя теорема единственности аналитических функций. Нули аналитических функций.

Теорема. Если a нуль аналитической функции ( не тождественно равной нулю ), то существует n такое, что f(z)=(z-a)ⁿg(z), где g(z)-аналитическая функция в точке a, не равная нулю в некоторой окрестности точки a.

Доказательство следует из формулы Тейлора разложения функции в окрестности точки a.

, в качестве n возьмем индекс первого, отличного от нуля коэффициента a_k

.

Отсюда следует, в частности,

Теорема. Если f(z) аналитическая в точке a, f(a)=0 и не является тождественным нулём, то этот нуль изолирован.

Ещё одно следствие.

Теорема. Если f(z) и g(z) аналитические в области D и совпадают на некоторой последовательности точек a_k aD , то f(z)g(z) в D.

Для доказательства рассматривается функция h(z) = f(z) – g(z), имеющая a не изолированным нулем. Из предыдущей теоремы следует h(z) 0.

2.Принцип максимума модуля аналитической функции.

Теорема. Если не тождественно постоянная функция f(z) аналитична в односвязной области D и непрерывна в DD, то её модуль не может достигать максимального значения в области D.

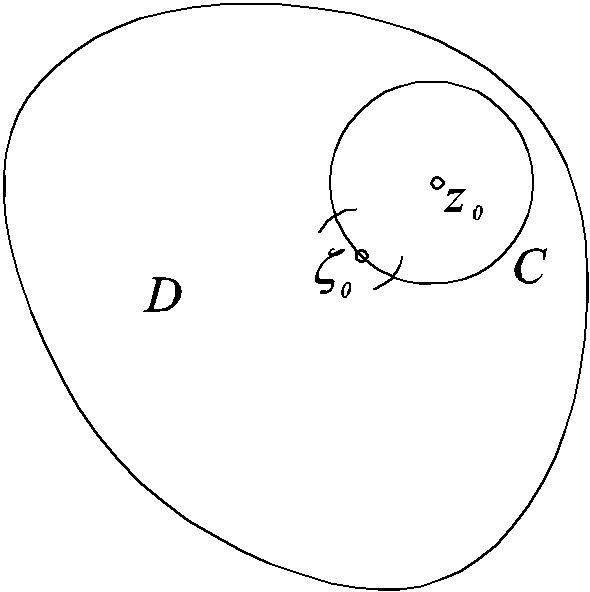
Доказательство. Противное, пусть и существует окружность С с центром в z₀, на которой не все значения |f(z)|=M . Иначе функция является постоянной в круге с центром в z₀ максимально возможного радиуса. Тоже самое можно сказать про любую точку границы этого круга, внутренней по отношению к области D. Таким образом, можно доказать постоянство функции во всей области D. Пусть ₀С и |f(₀)|<M, существует некоторая окрестность этой точки на окружности, где

|f()|<M-, U(₀)C

По теореме о среднем 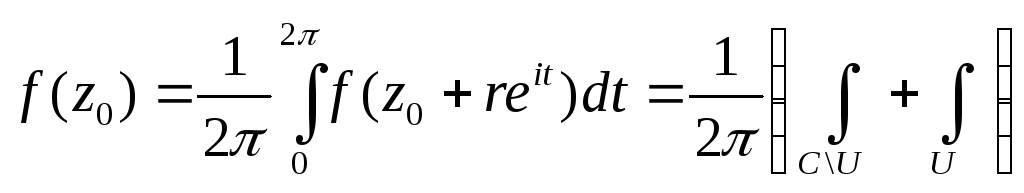. Отсюда

.

3.Терема Вейерштрасса

Теорема 1. Если ряд аналитических в области D функций f_k(z), f(z)=f_k(z) равномерно сходится на любом компакте KD, то

1. f(z) аналитическая в D

2. f^(p)(z)= f_k^(p)(z),p=1,2,…(*)

3. ряд (*) равномерно сходится на любом компакте K D.

Доказательство. Рассмотрим окружность окрестность U точки z₀ , лежащую в D со своим замыканием. Границу U ориентированную положительно обозначим С .

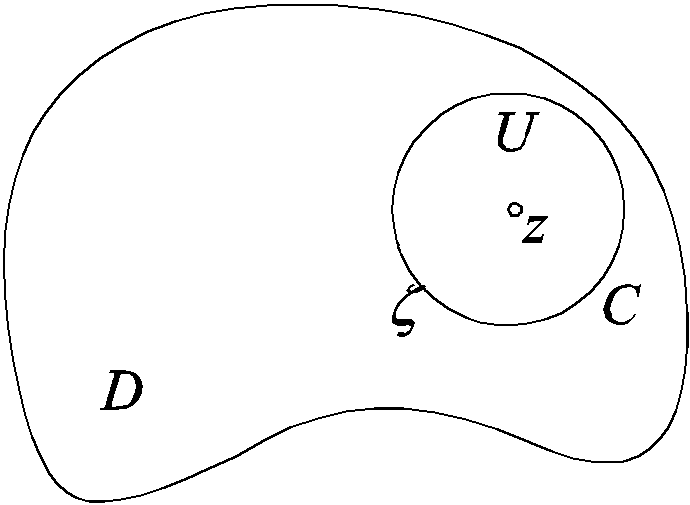
f()= f_k() непрерывна на C . Рассмотрим интеграл типа Коши

, эта функция аналитична в U и там

, ряд

сходится равномерно на C, следовательно, его можно почленно интегрировать.

, в частности, F(z)= f_k(z)=f(z). В силу произвольности z доказанное утверждение распространяется на все точки из D.

Равномерную сходимость ряда из производных будем доказывать только в частном случае, именно, когда K является замкнутым кругом радиуса r₀, лежащем в D . Несколько увеличим радиус этого круга так, чтобы вновь полученный круг K^* радиуса r также лежал в D . Границу этого круга, ориентированную положительно обозначим C.

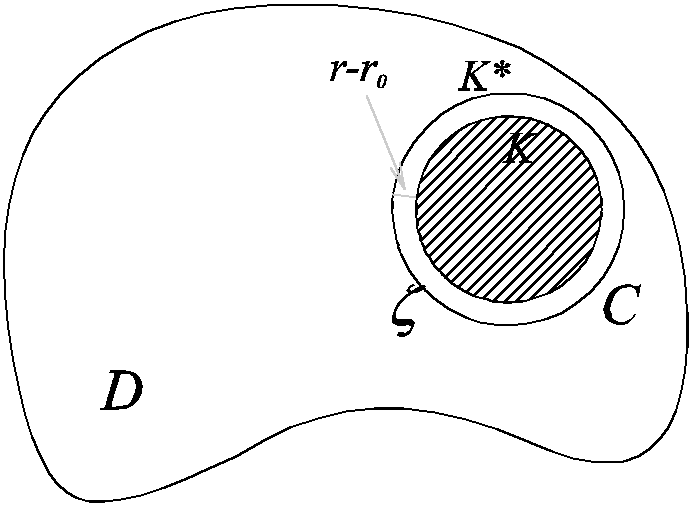
Тогда для всех zK будет выполнено

.

Теорема 2. Если ряд f(z)= f_k(z) аналитических в области D со спрямляемой границей D и непрерывных в замыкании DD функций f_k(z) равномерно сходится на границе D, то этот ряд равномерно сходится в D.(доказано только для любого компакта лежащего в D)

Доказательство. умножим на

, таким образом

zD:F(z)=f(z). Пусть компакт K D и  - расстояние от K до границы D, l – длина этой границы. Тогда для zK

§3 Ряды Лорана

Определение. Ряд вида называется рядом Лорана. называется правильной частью, называется главной частью ряда Лорана. Областью сходимости такого ряда ( в случае реального присутствия членов с отрицательными показателями ) будет кольцо r<|z-z₀|<R, в частности, может быть r=0, R=.

Из свойств степенных рядов следует, что ряд Лорана сходится равномерно на любом компакте, лежащем в кольце r<|z-z₀|<R , в частности, ряд Лорана можно почленно интегрировать по кривым, лежащим в кольце сходимости. Из соответствующего свойства степенных рядов следует возможность почленного дифференцирования ряда Лорана.

Теорема Лорана. Если функция f(z) – аналитическая в кольце К: 0 r₀ <|z-z₀|<R₀ , то

,где

С_ - окружность {| - z₀|=, r₀ < <R₀ }

Доказательство. Выберем кольцо r<|z-z₀|<R так, что r₀ < r, R < R₀ . Окружности с центром z₀ радиусами r, R , положительно ориентированные, обозначим C_r , C_R .

По формуле Коши для области с границей выполнено равенство

Для 

(2)

.

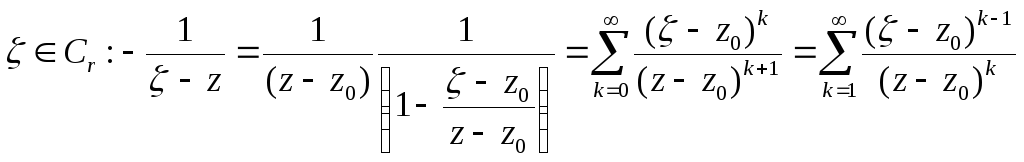
Интегралы и равны, соответственно, , k0,,k<0.

Теорема. Разложение в ряд Лорана единственно.

Доказательство. Отметим, что справедлива

Лемма Имеет место равенство

Доказательство леммы. =

2r^m+1. Откуда и следует требуемое равенство.

умножая на получим . Интегрируя последнее равенство по C_ , получим 2ic_n=2ib_n. Для этого интегрирования равномерная сходимость внутри кольца на окружностях есть.

Теорема. Имеет место неравенство

.

Доказательство.

§4 Изолированные особые точки однозначных аналитических функций.

Определение. называется изолированной особой точкой ( и.о.т.) функции f, если существует проколотая окрестность этой точки, где функция аналитична.

Пример. z+1/(z-1) изолированные особые точки 1, .

Определение. И.о.т. a называется устранимой, если существует конечный предел , полюсом, если , существенно особой точкой, если предел не существует.

Теорема. Для того, чтобы и.о.т. a была устранимой необходимо и достаточно, чтобы разложение в ряд Лорана в этой точке не содержало отрицательных степеней z-a

отсутствовала главная часть.

Достаточность очевидна. Необходимость.

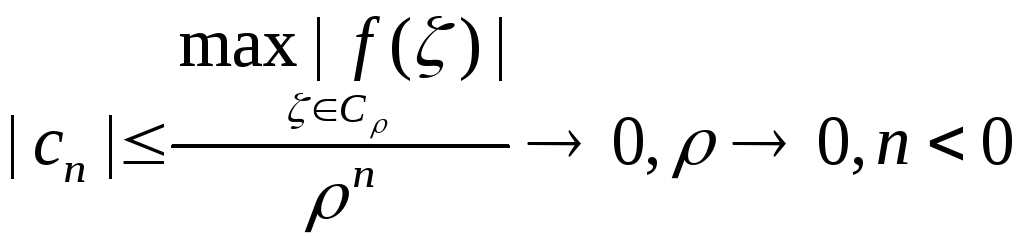
Следствие. После доопределения по непрерывности функция становится аналитичной в данной точке.

Теорема. Для того, чтобы и.о.т. была полюсом необходимо и достаточно, чтобы в разложении в ряд Лорана присутствовала главная часть следующего вида

.

Достаточность очевидна. Необходимость. Дано , тогда a есть изолированный нуль функции g(z)=1/f(z)=(z-a)ⁿ h(z), h(z)0 в окрестности a.

Определение. Порядком полюса a функции f называется порядок нуля a функции 1/f(z).

Следствие. Для полюса a порядка n, имеет место разложение

Определение. Порядком полюса z= функции f(z) называется натуральное число n, равное наибольшей из положительных степеней z с отличными от нуля коэффициентами в разложении.

, n – порядок полюса z=.

Теорема Соходского. Если - существенно особая точка функции f(z), то для .

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru