
Лекции / Курс лекций 2
.docТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru
Глава 2. Аналитические функции. Конформные отображения.
§1 Аналитические функции
-
Дифференцируемость. Условия Коши-Римана, моногенность.
f(z) – однозначная функция в области DC, w = f(z) = u(x,y) + i v(x,y), z = x + i y, z = x + iy, w = f = u + iv.
Определение. Моногенность
или существование производной в точке.
Существует конечный предел![]() .
.
Замечание: Для существования f(z0) необходимо и достаточно, чтобы в некоторой окрестности (проколотой) точки z0 имело место представление
w = A z + z, ( A = f(z0) ), - бесконечно малая.
Теорема. Для того, чтобы однозначная функция f(z) = u(x,y) + i v(x,y) была моногенной в точке z0 необходимо, а в случае дифференцируемости u, v и достаточно, выполнения условий Коши-Римана
![]()
Необходимость:
Возьмём z
= x,
тогда f(z0)
= ux +ivx.
Возьмём z
= iy, тогда
f(z0)
=
![]() uy
+i
uy
+i![]() vy
= vy -i uy. Сравнивая,
получим требуемые соотношения.
vy
= vy -i uy. Сравнивая,
получим требуемые соотношения.
Достаточность:
В силу дифференцируемости w
= u
+ i v
= uxx
+ uyy
+|z|+i(vxx
+ vyy)
+i|z|=
uxx
+ uyy
+i(-uy
x
+ ux
y)+|z|=
(ux -iuy)
x
+ (ux -iuy
)iy+|z|=(ux
-iuy)
z+|z||=(ux
-iuy) z+
![]() z=Az+z.
z=Az+z.
Замечание 1. Как это следует из доказательства в случае дифференцируемости u и v имеет место равенство
w = uxx + uyy +i(-uy x + ux y)+z
Замечание 2. Можно показать,
что uxx
+ uyy
+i(vxx
+ vyy)
=
![]() .
Действительно: x
=
.
Действительно: x
=![]() ,y
=
,y
=
![]() ,
x=
,
x=![]() , y
=
, y
=
![]() ,
f=uxx+uyy+
i(vxx+vyy)+|z|,
f=u(
,
f=uxx+uyy+
i(vxx+vyy)+|z|,
f=u(![]() ,
,![]() )+iv(
)+iv(![]() ,
,![]() ),
поэтому
),
поэтому
![]() ,
,
![]() ,
,
![]()
![]()
Замечание 3. Выполнение
равенства
![]() и условий Коши-Римана эквивалентно
равенству
и условий Коши-Римана эквивалентно
равенству
![]() .
.
Замечание 4. Как видно из предыдущего, если функция f дифференцируема в смысле действительного анализа, то
![]()
Фиксируем z=|z| ei. Производная в этом направлении
![]() существует и зависит от ,
если
существует и зависит от ,
если
![]() .
Таким образом у моногенной функции
производная не зависит от направления.
.
Таким образом у моногенной функции
производная не зависит от направления.
-
Голоморфные функции. Аналитичность.
Однозначная функция w=f(z) комплексного переменного, дифференцируемая в некоторой окрестности точки z0 называется аналитической в точке z0.
Функция называется голоморфной в области D, если она аналитична в каждой точке области D. Иногда говорят об аналитичности в области.
Так же, как для пределов действительных функций и производных действительных функций доказываются обычные свойства пределов и правил дифференцирования. Например, имеют место следующие свойства:
-
сумма двух аналитичных в точке функций будет аналитичной функцией в этой точке и (f(z) + g(z))=f(z)+g(z)
-
аналогичные свойства для произведения и частного (выписать формулы дифференцирования ), таблица производных.
В частности, многочлены и рациональные функции ( дать вначале определение рациональной или , что то же, дробно рациональной функции ).
-
Сложная функция. Пусть w=g(),=f(z), g аналитична и однозначна в , а f аналитична в D и осуществляет однозначное отображение D в , тогда суперпозиция w=g(f(z)) аналитична в D. Справедливо обычное правило дифференцирования сложной функции.
-
Теорема. Сумма степенного ряда есть аналитическая функция внутри круга сходимости и в этом круге ряд можно почленно дифференцировать.
Доказательство: Отметим вначале, что
![]() ,
,![]()
![]() для доказательства того, что
радиус остаётся тем же
для доказательства того, что
радиус остаётся тем же
![]()
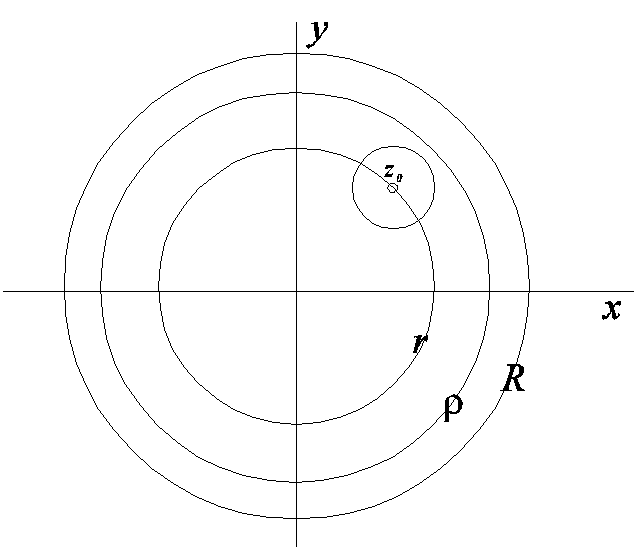
Пусть r=|z0|, выберем , удовлетворяющее условию r<<R, где R -радиус сходимости, |z|=|z-z0|<-r
Степенной ряд сходится абсолютно при z=, поэтому для заданного >0
:![]() .
.
Для этого N
выбираем
<-r
так, чтобы при |z-z0|<
выполнялось неравенство
![]() ,
,
тогда при |z-z0|<
будет выполнено неравенство
![]() .
Действительно, имеем
.
Действительно, имеем
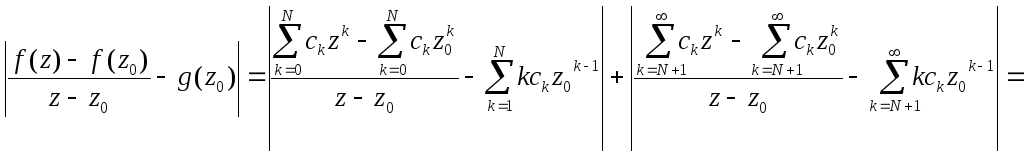
![]()
![]() <
<![]()
![]() <
<![]() +
+![]() <
<![]()
![]() < .
< .
Следствие 1. Степенной ряд можно почленно дифференцировать в круге сходимости любое число раз.
Следствие 2. Если степенной
ряд
![]() сходится в круге |z-z0|<R,R>0
к функции f(z),
то
сходится в круге |z-z0|<R,R>0
к функции f(z),
то
![]() Доказательство: дифференцировать нужное
число раз и подставить z=z0.
Доказательство: дифференцировать нужное
число раз и подставить z=z0.
Определение. Если f(z)
имеет производные любого порядка, то
ряд
![]() называется рядом Тейлора функции f(z).
Как это видно из Следствия 2, ряд
называется рядом Тейлора функции f(z).
Как это видно из Следствия 2, ряд
![]() является рядом Тейлора своей суммы. Из
Следствия 2 также следует теорема
единственности разложения в степенной
ряд:
является рядом Тейлора своей суммы. Из
Следствия 2 также следует теорема
единственности разложения в степенной
ряд:
Теорема. Если два ряда
![]() и
и
![]() совпадают в круге |z-z0|<R,R>0,
то ak=bk.
совпадают в круге |z-z0|<R,R>0,
то ak=bk.
Определение. Функция f(z) называется регулярной в точке z0 если она определена в окрестности точки z0 и в некоторой окрестности этой точки
![]()
Функция называется регулярной в области, если она регулярна в каждой точке этой области.
§2 Конформные отображения
-
Существование обратной функции для аналитической функции в окрестности точки
Пусть f(z) = u(x,y) +iv(x,y) аналитична в точке z0 и f(z0)0
w=f(z):![]()
![]() в окрестности т. z0.
в окрестности т. z0.
Существует обратная функция
в некоторой окрестности точки w0=f(z0),
z=f-1(w),
причём
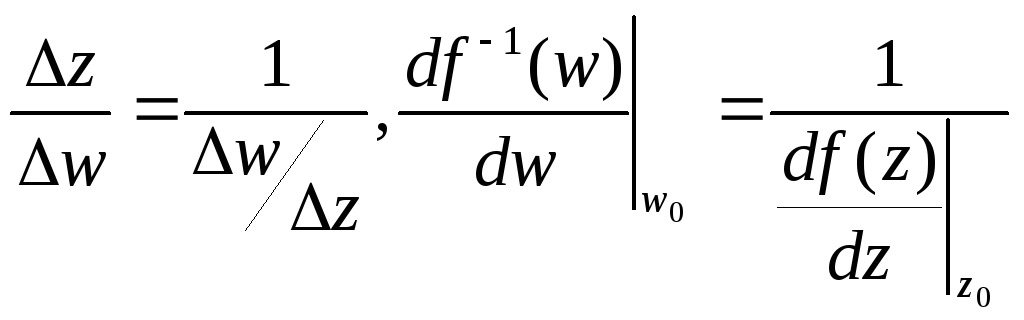 .
.
-
Геометрический смысл аргумента производной.
Пусть -гладкая кривая Жордана, заданная уравнением z(t)=x(t)+iy(t),t[,],z’(t)0,t0(,).Обозначим образ кривой при отображении f. Предположим, что f(z) аналитическая в точке z0 функция и f(z0)0.
Имеем : w(t)=f[z(t)],w(t0)=f(z0)z(t0) и Arg f(z0) = arg w(t0) – arg z(t0)
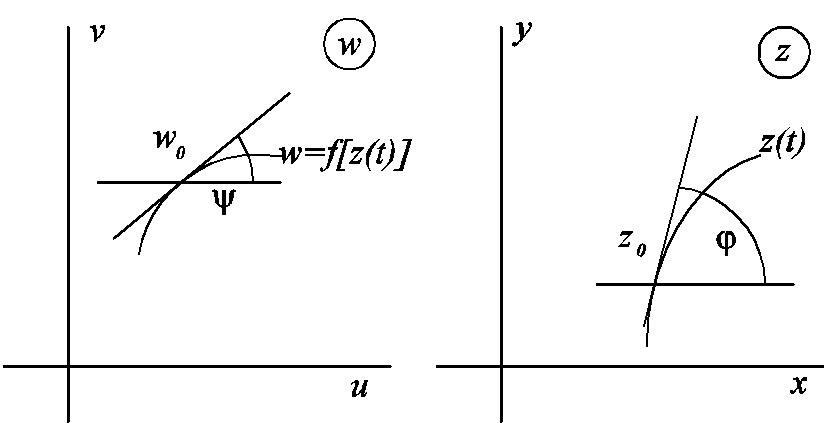
arg z(t0) = , arg w(t0) = - главные значения аргументов, Arg f(z0) - угол поворота кривой в точке z0 при отображении w = f(z), определяемой с точностью до 2k. Как видим, этот угол не зависит от выбора кривой, проходящей через данную точку. В частности, если в плоскости z пересекаются две кривые z1(t), z2(t), имеющие в точке пересечения главные значения аргументов 1, 2, а их образы при отображении w=f(z), соответственно углы 1, 2, то мы получим
2 - 2 =arg f(z0)+2k2, 1 - 1 =arg f(z0)+2k1, откуда, вычитая одно равенство из другого, получим 2 - 1 =2(k2- k1)+ 2 - 1. Полученное равенство позволяет сформулировать следующее
Следствие: При сделанных предположениях ( аналитичность в точке и неравенство нулю производной ) углы при отображении сохраняются. Кроме того сохраняется «порядок обхода». Например, если поворот от касательной к первой кривой в точке пересечения к касательной второй кривой в плоскости z происходит против часовой стрелки, то тоже самое будет наблюдаться и в плоскости w между образами этих кривых.
-
Геометрический смысл модуля производной.
z=x+iy,w=u+iv
![]() ,
dw=f(z0)dz,
,
dw=f(z0)dz,
![]()
Коэффициент растяжения кривой в точке, не зависит от этой кривой и равен |f(z0)|. Это свойство называется свойством сохранения масштаба в точке z0.
-
Конформные отображения.
Определение (Конформность в C). Непрерывное, взаимно однозначное отображение w=f(z) области D на область D* называется конформным, если в каждой точке D имеет место
-
свойство сохранения углов
-
сохранение масштабов
в перечисленном выше смысле.
Как мы видели, если f(z) аналитична в точке z0 и f(z0), то отображение w=f(z) конформно в некоторой окрестности точки z0.
Определение. Углом между
кривыми z1(t),
z2(t),
в бесконечности ( предполагается, что
![]() ) называется угол в 0
между образами этих кривых при отображении
w=1/z,
то есть между кривыми
) называется угол в 0
между образами этих кривых при отображении
w=1/z,
то есть между кривыми
![]() в
т. 0. Изменение масштаба в
находится аналогичным образом,
предварительно переведя
в точку 0
отображением w=1/z.
в
т. 0. Изменение масштаба в
находится аналогичным образом,
предварительно переведя
в точку 0
отображением w=1/z.
|
Решение задач с преобразованиеv углов и масштабов при отображении w=f(z) |
|
|
Задача |
Решение |
|
1. z0,f(z0) |
См. f(z0) |
|
2. z0,f(z0) |
См. w1=f(1/w) в точке w0 0 |
|
3. z0,f(z0) |
См.
|
|
4. z0,f(z0) |
См.
|
Пример 1. Исследовать на
конформность функцию
![]() в
расширенной комплексной области.
в
расширенной комплексной области.
Решение. В точках отличных от i и конформность следует из существования производной и не равенства её нулю.
В точке z=i
значение функции w=,
поэтому для исследования в этой точке
нужно рассмотреть функцию
![]() в точке z=i,
(см. таблицу п. 3 ). Конформность следует
из существования производной и не
равенства её нулю при z=i.
в точке z=i,
(см. таблицу п. 3 ). Конформность следует
из существования производной и не
равенства её нулю при z=i.
В точке z=
значение функции w=1,
поэтому для исследования на конформность
в этой точке следует «бесконечность в
аргументе» перевести предварительно
в 0 (или,
что то же заменить
на 0 с
помощью замены переменного
![]() ).
Таким образом, для исследования берётся
функция
).
Таким образом, для исследования берётся
функция
![]()
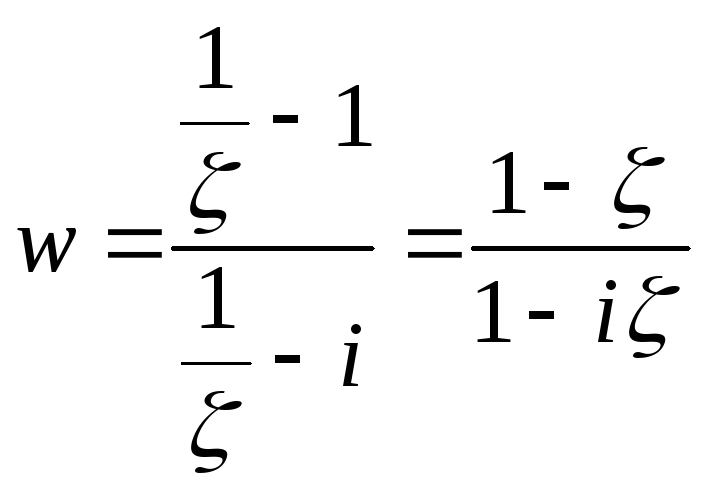 в точке 0,
которая в этой точке имеет производную,
отличную от нуля.
в точке 0,
которая в этой точке имеет производную,
отличную от нуля.
Пример 2. Исследовать на конформность в точке z= функцию w=iz-2.
Решение. Во всех точках z
производная существует и не равна нулю.
При z=
, w=,
поэтому, согласно определению, необходимо
сделать две замены:
![]() ,
и
,
и
![]() .
В итоге, для исследования на конформность
имеем функцию
.
В итоге, для исследования на конформность
имеем функцию
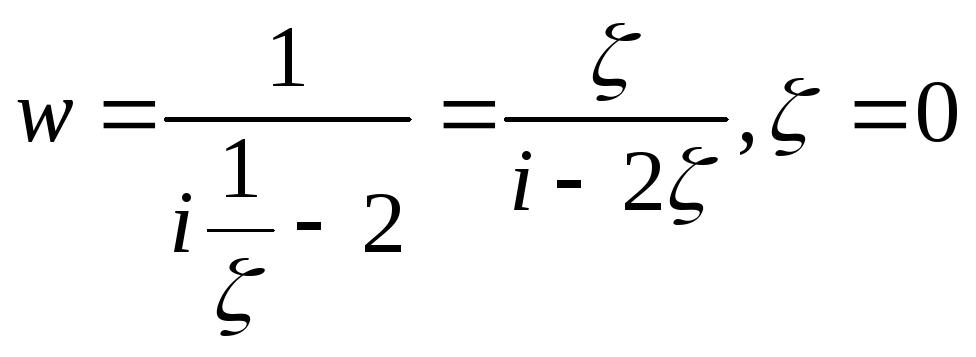 .
Эта функция в точке =0
имеет производную не равную нулю.
.
Эта функция в точке =0
имеет производную не равную нулю.
Пример 3: Докажем непосредственно
свойство сохранения углов в т. 2i
при отображении
![]() .
.
Пусть z1(t)
и z2(t)
выходят из точки 2i.
Для первой кривой t1,1,
для второй t2,2.
Точка 2i
переходит в бесконечность, поэтому
будем искать углы между кривыми
![]() и
и
![]() в
точках 1,
2,
соответственно. Для этих кривых имеем
в
точках 1,
2,
соответственно. Для этих кривых имеем
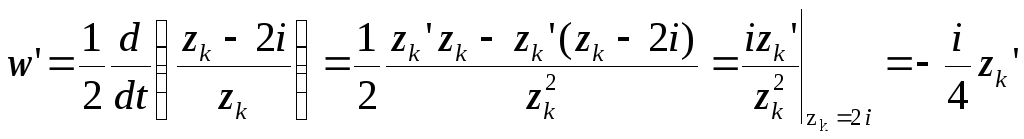 ,
поэтому угол между образами wk
в бесконечности будет равен:
,
поэтому угол между образами wk
в бесконечности будет равен:
![]()
Некоторые свойства конформных отображений ( без доказательства )
Свойство сохранения области. Если f(z) аналитична и однолистна (взаимно однозначна) в области D, то f(z)0 в D и f(z) конформно отображает D на D* и f -1(w) аналитична в D* ( где D* образ D при отображении f(z)).
Свойство сохранения границ.
Пусть D и D*
две области, ограниченные замкнутыми
кривыми Жордана
D и
D*.
Если f(z)
отображает D на D*
конформно, то она отображает
![]() на
на
![]() взаимно однозначно и взаимно непрерывно
с сохранением ориентации обхода границы.
взаимно однозначно и взаимно непрерывно
с сохранением ориентации обхода границы.
Свойство взаимно однозначного соответствия. Пусть D и D* две односвязные области, ограниченные замкнутыми кусочно-гладкими кривыми Жордана D и D* . Если аналитическая в D функция взаимно-однозначно и непрерывно отображает D на D* с сохранением обхода, то эта функция конформно отображает D на D*.
Теорема ( Риман ). Если граница односвязной области DC состоит более, чем из одной точки, то существует аналитическая функция, конформно отображающая D на внутренность круга |z|<1, причём эта функция единственна, если задать условия нормировки ( например, перевести заданную точку z0 с заданным направление в заданную точку w0 с заданным направлением.
ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

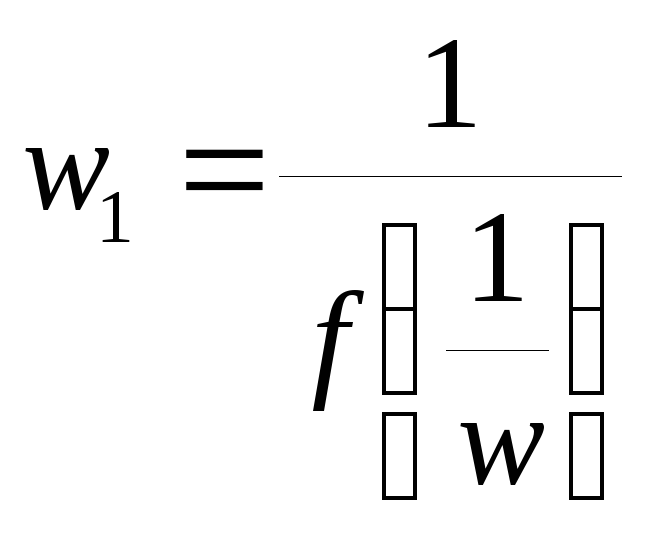 в точке w0
0
в точке w0
0