Лекции / Курс лекций 3

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

Глава 3. Примеры конформных отображений

§1 Дробно линейное отображение

1. Линейная функция.

w = az + b, a0

Можно представить, как суперпозицию отображений: w₁=|a| z, w₂=e^{i arg a} w₁, w = w₂+b. Взаимно однозначно и конформно отображает на

См. пример в разделе Конформные отображения.

Определение. Окружностью в будем называть окружности, либо прямые.

Уравнение окружности на комплексной плоскости

A(x²+y²)+Bx+Cy+E=0, .

Подставляя получим эквивалентную форму представления окружности или, , .

Круговое свойство. Линейная функция сохраняет окружности. (очевидно, см. суперпозиции ). Про растяжение доказать со ссылкой на общее уравнение окружности. Подставить в уравнение окружности.

2. Преобразование инверсии.

Определение. Точки z, z* называются симметричными относительно окружности  на C, если они лежат на луче, выходящем из центра окружности и произведение расстояний от этих точек до центра равно квадрату радиуса. Из условий |z*-z₀||z-z₀|=R², arg(z-z₀)=arg(z*-z₀) следует равенство, связывающее симметричные точки относительно окружности с центром в z₀ и радиуса R.

Способ построения симметричных точек виден из рисунка. Из подобия треугольников .

Теорема. Для того, чтобы точки z, z* были симметричны относительно , необходимо и достаточно, чтобы любая окружность  на , проходящая через них, была ортогональна .

Доказательство. Отметим известное свойство касательных и секущих к окружности: квадрат касательной равен произведению секущей на ее внешнюю часть. Необходимость. Пусть  - некоторая окружность, проходящая через симметричные точки. Проведем одну из касательных к окружности  из точки z₀ . Обозначим точку касания . Если точки симметричны, то по сформулированному свойству секущей касательная будет равна R², то есть точка  точно попадёт на окружность . Следовательно отрезок соединяющий z₀ и  , с одной стороны будет радиусом к  , а с другой стороны касательной к .

Достаточность. Если любая  , проходящая через точки z, z* ортогональна , то беря в качестве  прямую получим, что точки лежат на луче, выходящем из центра. Проведем какую-нибудь окружность  через точки z, z* . Обозначим любую из точек пересечения окружностей ,  через . Так как окружности ортогональны, то отрезок z₀ ,  будет и радиусом для  и касательной для  . По упомянутому свойству касательной, получим равенство |z*-z₀||z-z₀|=R².

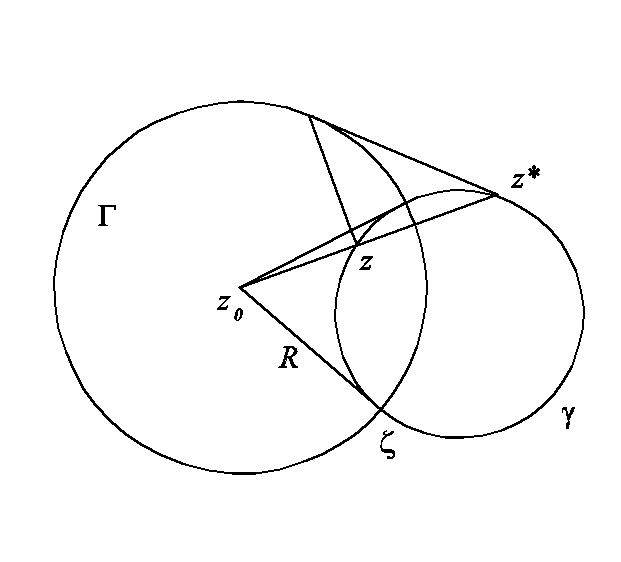
Доказанная теорема позволяет переформулировать определение симметричных точек так, что его можно использовать в расширенной комплексной плоскости.

Опр. Точки z, z* называются симметричными относительно окружности  на , если любая окружность, проходящая через эти точки, ортогональна к .

В таком виде определение совпадает и с обычной симметрией относительно прямых.

Определение. Отображение zz*, переводящее z в симметричную z* (естественно считаем, что центр переходит в  и наоборот ) относительно , называется симметрией относительно окружности или инверсией.

3. Отображение .

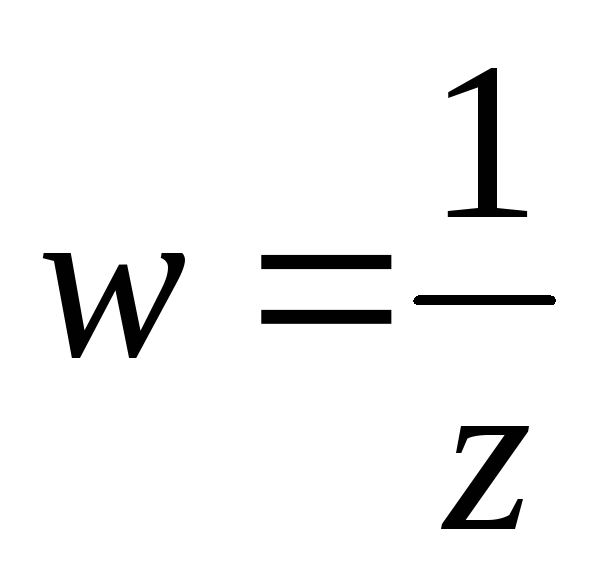Это отображение переводит окружности в в окружности. Действительно пусть дана окружность в :, подставим в это уравнение , получим или .

Отображение является конформным на расширенной комплексной плоскости ( легко проверить в 0 и в бесконечности ).

Следствие. Симметрия может быть реализована как суперпозиция четырёх отображений: сдвиг, операция сопряжения, обратная, сдвиг и поэтому сохраняет окружности и антиконформна.

4. Дробно линейная функция.

Представление в виде суперпозиции простейших отображений.

,

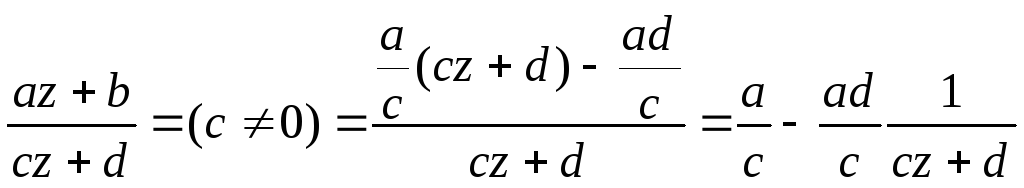Из предыдущих свойств следует, что дробно линейное отображение является конформным на расширенной комплексной плоскости и переводит окружности в окружности.

Теорема. Свойство сохранения симметричных точек. Дробно линейное отображение L переводит любые точки z, z*, симметричные относительно окружности  на , в точки w, w*, симметричные относительно образа L() этой окружности.

Доказательство. Если z, z* симметричны относительно , то это означает, что все , проходящие через них, ортогональны . Так как L сохраняет углы и окружности, то любая окружность, проходящая через w, w*, будучи образом некоторой , будет ортогональна L(), что означает симметрию.

Свойства дробно линейных отображений

1) Взаимно однозначное и конформное отображение всей расширенной комплексной плоскости z на всю расширенную комплексную плоскость w. Обратное так же дробно линейное (легко проверить)

2) Суперпозиция двух дробно линейных отображений есть дробно линейное отображение

Отметить, что «якобианы» при суперпозиции перемножаются.

тогда

(легко проверить)

3) Круговое свойство и сохранение симметрии. Произвольное дробно линейное отображение L переводит любые точки z, z*, симметричные относительно какой-нибудь окружности  на , в точки w, w*, симметричные относительно образа =L() этой окружности.

4) Каковы бы ни были три различные точки z₁,z₂,z₃C и три различные точки w₁,w₂,w₃C, существует единственное дробно линейное отображение L такое, что L(z_k)=w_k, k=1,2,3.

Доказательство.

, z₁0, z₂, z₃1,

, w₁0, w₂, w₃1,

Единственность.

Лемма. Если дробно линейное отображение переводит точки 00,, то оно тождественное.

Доказательство. Из 00 b=0, ( при этом можно считать, что a=1 ) таким образом, отображение должно иметь вид .  c=0, ,11 d=1.

Предположим, что ещё одна функция w=f(z) обладает этим свойством. Тогда оставляет на месте 0,,1. Такое отображение, как это легко увидеть, является тождественным , откуда следует, что .

5) Непосредственной проверкой можно убедится, что

§2 Степенная функция w=zⁿ, n-натуральное.

1.Отображение степенной функцией.

w=zⁿ=rⁿe^in. Область однолистности: ,|z₁|=|z₂|,n arg z₁ = n arg z₂ + 2k, arg z₁ = arg z₂ = 2k/n. Каждую из областей D_k:2k/n < arg z < 2(k+1)/n функция w=zⁿ отображает на плоскость с вырезом по положительной части действительной оси.

2.Обратная функция.

Определение. Функция f(z) называется ветвью на множестве D многозначной функции F(z), определённой на D, если f(z) однозначная, непрерывная функция, совпадающая с одним из значений F(z) в каждой точке zD.

Обратная функция многозначна ( n различных корней, если w0 )

. Рассмотрим n экземпляров плоскости C_w с разрезом по положительной части вещественной оси, будем их обозначать D*_k , k =0,1,…,n-1. Определим ветвь следующим образом: фиксируем некоторую точку w_kD*_k и для её образа выбираем значение

,

Определим ветвь g_k(w) на D*_k: именно, если w D*_k, то положим

, где arg w получен из arg w_k непрерывным изменением вдоль какой-либо кривой, соединяющей w и w_k. Можно показать, что конечное значение arg w не будет зависеть от конфигурации пути, поэтому определение корректно. Таким образом можно выделить n однозначных ветвей для функции . Обозначают эти ветви . Ветвь соответствующая k есть конформное отображение D*_k на область 2k/n<arg z<2(k+1)/n.

Замечание. При полном обходе вокруг начала координат arg w получает добавку 2 и мы приходим к другому значению z. Такие точки называются точками ветвления. Для данной функции кроме 0 точкой ветвления является .

3. Понятие римановой поверхности для функции

Два листа D*₀ , D*₁ склеены, как показано. Двигаясь по ₀, а потом по ₁ при обходе по ₀ обходим по ₀ полный обход по верхнему листу и переход на нижний лист. В результате вся плоскость C_z взаимно однозначно отображается на D*₀  D*₁ (поверхность Римана ).

Определение. Если в любой окрестности точки aС существует замкнутая Жорданова кривая , содержащая внутри ограниченной кривой области точку a такая, что при обходе , начиная с точки z₀  ( и непрерывном изменении модуля и аргумента ) значение ветви f_k(z₀) многозначной функции F(z) переходит в значение другой ветви f_l(z₀), то точка a называется точкой ветвления.

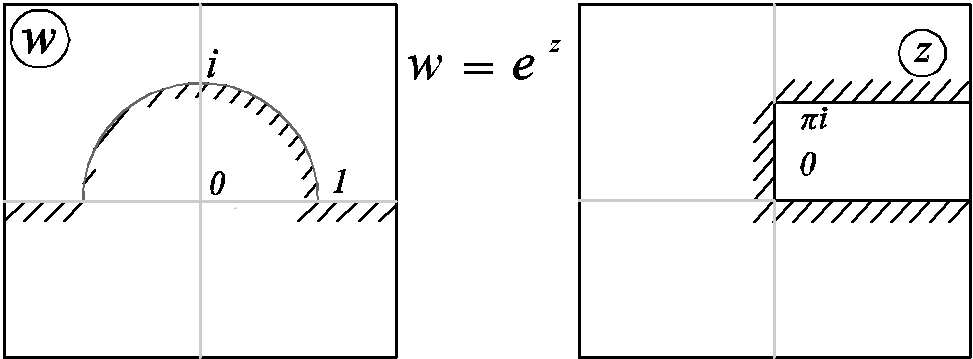
§3 Функция w=e^z

1.Отображение

w=u+iv=e^xe^iy, |w|=e^x, arg w = y

Однолистность exp(z₁)=exp(z₂), x₁=x₂, y₁=y₂+2k

Область D_k={z:2ki < Im z < 2(k+1)i }

2.Обратная функция.

Если w=e^z, то |w|=e^x, x=ln |w|, arg w = y откуда для обратной функции z = Ln w = ln|w|+i Arg w = ln|w|+i (arg w + 2k ), при k=0 получаем ln w.

Ветви, поверхность Римана.

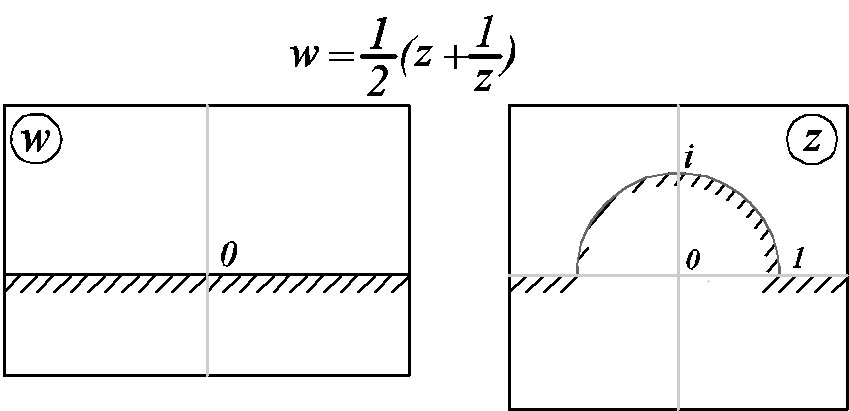
§4 Функция Жуковского

Определена, однозначна и аналитична всюду в C кроме z=0.

,w0 при z1, таким образом, эта функция конформна в любой точке кроме z=1, ( конформность в 0 и в  проверить самостоятельно )

Область однолистности откуда либо z₁=z₂, либо z₁z₂=1. Областью однолистности является, например, каждое из следующих множеств |z|<1, |z|>1, Im z > 0.

Пусть z=r ( cos  + i sin  ) = r e^i, тогда

(1)

Следовательно, окружность r=r₀ переходит в эллипс с полуосями . Фокусы c =  1.

Из (1) следует, что лучи arg z =  переходят в гиперболы с фокусами 1. Асимптоты гипербол v = u tg . Функция Жуковского переводит внешность единичного круга на плоскость с разрезом по отрезку [-1,1].

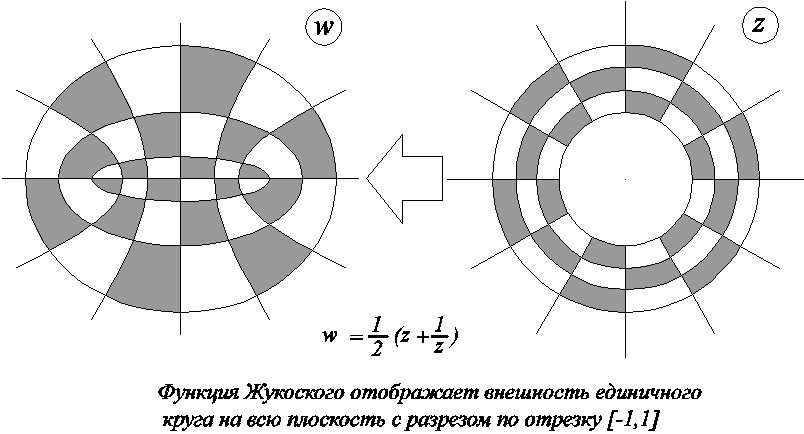
2.Обратная функция

. Рассмотрим область , плоскость с разрезом. Первая однозначная ветвь f₁(w) переводит D* в |z|<1, вторая ветвь f₂(w) переводит D* в |z|>1. Точки w=1.

§7 Таблица некоторых конформных отображений.

1)симметричная относительно единичной окружности , поэтому образом единичной окружности будет единичная окружность.

2) Верхняя полуплоскость на единичный круг..

3) Угол {z: arg z (0, ),0<<2} на верхнюю полуплоскость . Напоминание .

4) В частности w=z² отображает первый квадрант на верхнюю полуплоскость.

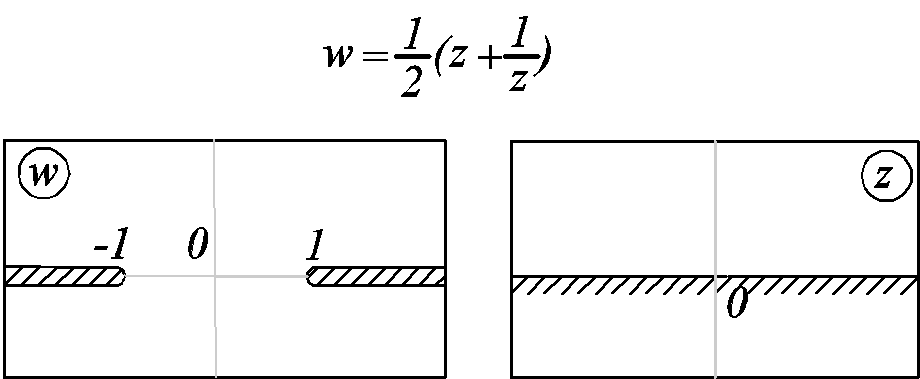
5) Плоскость с разрезом по положительной части вещественной оси на верхнюю полуплоскость

6)

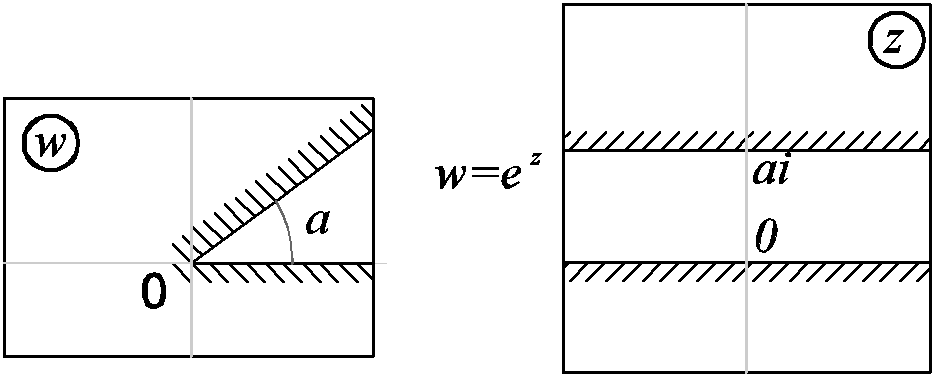
7) Частный случай

8) Частный случай

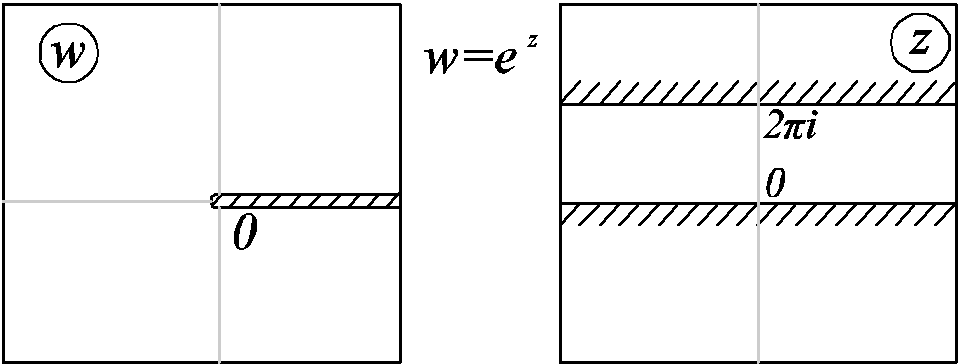
9)

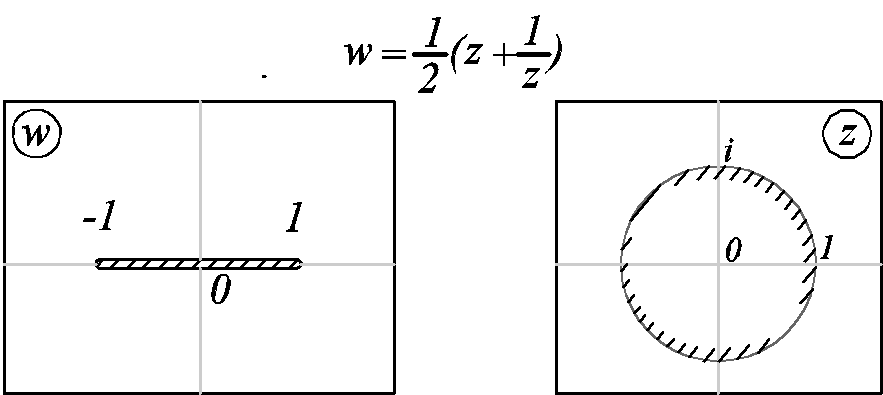
10)

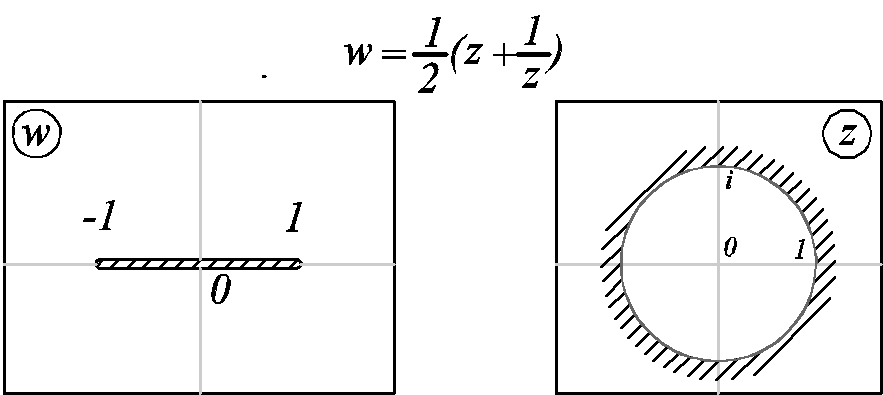
11)

12)

13)

14)

Пример. Отобразить область

Решение

Пример.

(нужная ветвь) на верхнюю полуплоскость, затем w₂=w₁².

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru