8. Момент силы относительно оси.
Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси.
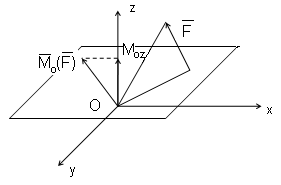
Если момент силы относительно некоторого центра О вызывает вращательное движение тела вокруг этого центра, то момент силы относительно оси вызывает вращение тела вокруг данной оси.
При решении задач моменты сил относительно осей удобно вычислять наглядным способом по правилу:
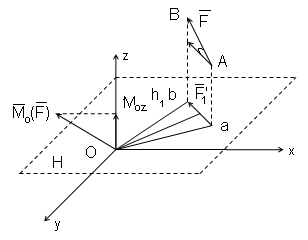
Проводим плоскость и произвольно и перпендикулярно к оси OZ и находим точку О, пересечения этой плоскости осью.
Проектируем силу на отмеченную плоскость.
Вычисляем момент проекции
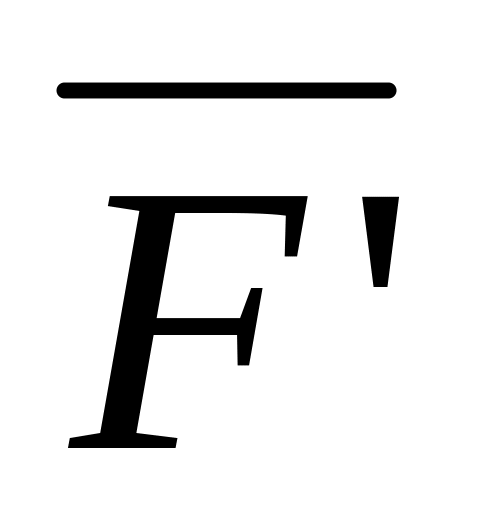силы
на эту плоскость относительно точки
О:
При этом моменты силы относительно оси
считается положительным, если наблюдатель
видит со стороны положительного
направления оси OZ, что
сила
пытается вращать тело вокруг оси OZ
против стрелки часов.
Численно момент будет равен:
Параллельные силы.
1.Сложение параллельных сил, которые направлены в одну сторону
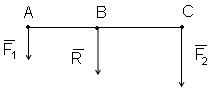
Равнодействующая этих сил (её модуль) будет равна:
Линия действия равнодействующей в этом случае пересекает отрезок АВ в точке С, которая делит этот отрезок на части, обратно пропорциональные модулям сил:
Т.е равнодействующая двух параллельных сил, направленных в одну сторону, по одну сторону, по модулю равна сумме модулей этих сил, направлена в ту же сторону, что и силы, и делит расстояние между точками приложения сил на отрезки, обратно пропорциональные силам.
2.Сложение параллельных сил, направленных в противоположные стороны.
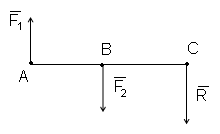
Равнодействующая двух параллельных сил, направленных в разные стороны, по модулю равна разнице модулей этих сил, направлена в сторону большей силы и делит расстояние между точками приложения обратно пропорционально модулям сил.
В том случае, если силы
,
то модуль равнодействующей равен нулю.
Однако действие пары сил на тело не равно нулю и вызывает вращательное движение.
Мерой вращательного движения пары сил служит момент пары, величина которого определяется по формуле:
[Hм]
В этом случае плечо h- это кротчайшее расстояние между линиями действия параллельных сил.
Направление вращения, созданного парой сил, определяет знак момента пары: если пара сил вращает тело против часовой стрелки- момент положительный, если наоборот- отрицательный.
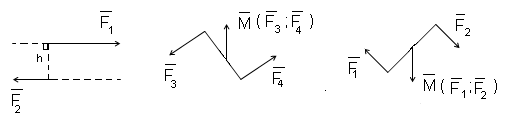
Момент пары сил имеет величину, направление и плоскость действия, т.е векторной величиной.
Вектор момента пары сил перпендикулярен к плоскости, в которой лежит, и направлен в ту сторону, откуда вращается тело, под действием пары в сторону против хода часовой стрелки.
Выводы:
Пару сил, не изменяя её действия на тело, можно перенести куда угодно в плоскости, в которой лежит пара.
Пару сил, не изменяя её действия на тело, можно перенести в параллельную плоскость.
В паре сил, не изменяя её момента, можно изменять соответственно модули сил и длину плеча.
Две пары сил с равными моментами эквивалентны.
Несколько пар сил, которые лежат в одной плоскости, можно заменить одной эквивалентной парой с моментом, который равняется векторной сумме моментов этих пар.
На основании пятого вывода можно записать:
На основании теоремы о проекциях суммы векторов можно записать:
;
;
;
Модуль момента пары:
Таким образом для равновесия пар необходимо и достаточно, чтобы вектор-момент равнодействующей пары был равен нулю:
т.е
;
;
Произвольная система сил.
Произвольной системой сил называется совокупность прилагаемых к твердому телу сил, лини действия которых произвольно ориентированы в пространстве.
Произвольную систему сил можно свести к одной равнодействующей силе, которая равна главному вектору, прилагаемому в центре сведения и к одной паре сил, которая равна главному моменту относительно того же центра:
;
Модули векторов
и
определяют
по формулам:
В результате для произвольной системы
сил твердое тело, находящееся под
действием этой системы, будет находиться
в равновесии, если главный вектор
и
главный момент
системы будут равны нулю:
;
Проектируя эти уравнения декартовы оси координат, запишем аналитические условия равновесия произвольной пространственной системы сил, читаются следующим образом:
для равновесия произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на три взаимно взаимно перпендикулярные оси и сумма моментов всех сил относительно этих осей равнялась нулю:
