Моделирование технологического потока

Основные принципы системного моделирования.

Модель должна иметь сходство с оригиналом, но это сходство не может быть полным, поскольку теряется специфика модели, и ее назначение. Вместе с тем модель не должна быть произвольной, не соответствующей оригиналу. В этом случае она не дает представления об оригинале и не может выполнять функцию модели. Диапазон сходства, подобия модели и ее объекта расположен - от абсолютного до нулевого. При абсолютном подобии моделирование отсутствует, поскольку имеются две идентичные системы. При нулевом подобии (отсутствии подобия) модели также нет, а имеются две абсолютно различные системы, которые ни в чем не повторяют друг друга.

Представить объект в виде системы - значит уложить его в некоторую схему, т. е. в определенном смысле упростить. Модель представляет собой упрощение, определенным образом схематизированное отражение моделируемой системы. Это упрощение может выражаться в значительном сокращении в модели числа компонентов оригинала с сохранением лишь некоторых его общих морфологических черт, в сокращении числа взаимосвязей компонентов оригинала и упрощении их внутреннего содержания, в схематизации пространственного порядка и следования во времени присущих оригиналу компонентов и процессов и т.д.

Моделирование строения технологического потока

Остановимся на особенностях моделирования строения объекта, применяя системный подход. На рис. схематично показана системная точка зрения исследователя на моделируемый технологический поток. Этот исследователь (метанаблюдатель) имеет возможность моделировать весь технологический поток как большую систему. Его помощники (наблюдатели) моделируют лишь часть потока.

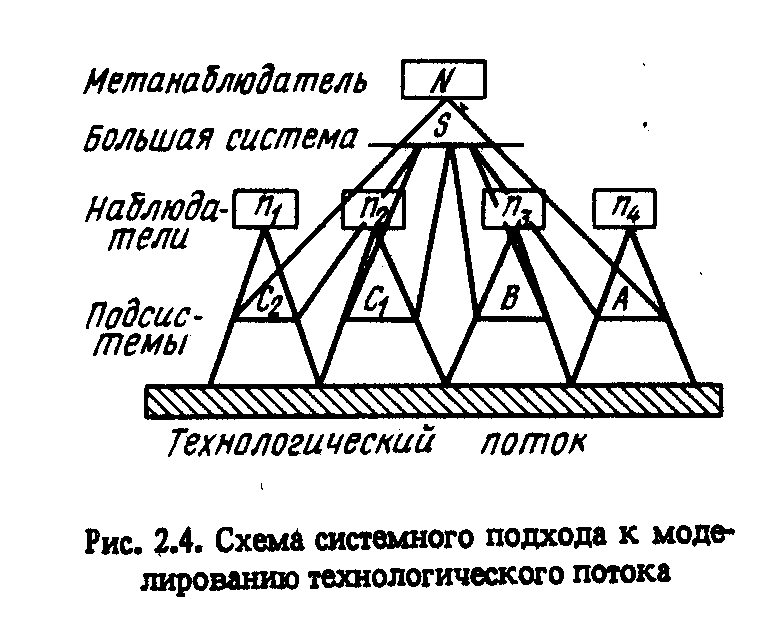
Рис. Схема системного подхода к моделированию технологического потока

Моделирование потока целесообразно тогда, когда исследователь должен решить сложную проблему, т. е. разрешить противоречие между необходимостью развития поточной линии и невозможностью это сделать с помощью современной техники и технологии.

Моделирование строения технологического потока как системы имеет своей конечной целью выявление его механизма функционирования и развития.

При моделировании строения сложный объект качественно расчленяется на ряд простых, а в процессе моделирования его функционирования взаимодействия этих простых объектов выражаются количественно. Разрешение сложного технического противоречия распадается на ряд задач, которые имеют хорошо отработанные методы решения.

Результатом моделирования строения технологического потока в линии являются рассмотренные операторные модели технологических систем ряда перерабатывающих производств.

Моделирование функций технологического потока

В математическом моделировании технологических процессов пищевого производства сформировалось два направления: теоретическое и статистическое. При исследований режимов работы линий рационально использовать оба направления, причем статистическое - на этапе исследования в рамках системы или ее подсистемы (макроисследование), а теоретическое - на этапе исследования в рамках элемента (микроисследование), т.е. при глубоком изучении процессов, протекающих в машине или аппарате.

В зависимости от характера и цели исследования применяются различные математические методы. При оптимизации процессов все они сводятся к тому, чтобы найти минимум или максимум поверхности, описываемой уравнением целевой функции.

Оптимизация процессов методами аналитическими, градиентными и математического программирования требует детерминированного описания. Подавляющее большинство процессов пищевых производств являются стохастическими и не имеют достаточно хорошо разработанной теории.

Для исследования режимов технологического потока весьма перспективны методы статистического описания, дающие возможность, абстрагируясь от неизученной сущности процесса, оптимизировать его.

Статистическое исследование стохастических процессов имеет два подхода. Первый из них - регрессивный анализ - базируется на обработке результатов так называемых "пассивных" экспериментов. Второй - на обработке результатов «активных» экспериментов.

В зависимости от того, входит параметр времени в качестве независимой переменной в уравнения математического описания или нет, все модели разделяют на стационарные и нестационарные. В связи с этим различают статическую оптимизацию, с помощью которой решаются вопросы создания к реализации оптимальной модели, и динамическую оптимизацию, цель которой - создание и реализация системы оптимального управления процессом.