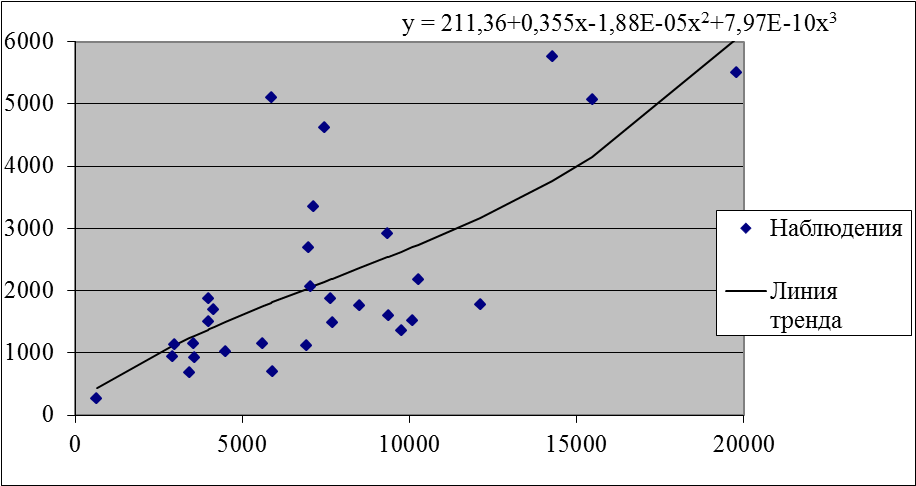
Полиномиальная модель 3-го порядка.
Уравнение регрессионной модели кубической
параболы выглядит следующим образом:
ŷ
= 211,36 + 0,354 * х - 1,879Е-5 * х2 + 7,97E-10 * x3.
Эта модель также отличается от линейной,
в матрице Х на 2 столбца больше: Х =
(n×4),
так как матрица B содержит
на 2 строки
больше B =
(4×1).
x |
y |
ŷ |
|||
1 |
637 |
405769 |
258474853 |
262 |
4,30E+02 |
1 |
2905 |
8439025 |
2,452E+10 |
941 |
1,10E+03 |
1 |
2966 |
8797156 |
2,609E+10 |
1128 |
1,12E+03 |
1 |
3407 |
11607649 |
3,955E+10 |
677 |
1,23E+03 |
1 |
3539 |
12524521 |
4,432E+10 |
1152 |
1,27E+03 |
1 |
3557 |
12652249 |
4,5E+10 |
917 |
1,27E+03 |
1 |
3973 |
15784729 |
6,271E+10 |
1496 |
1,37E+03 |
1 |
3986 |
15888196 |
6,333E+10 |
1875 |
1,38E+03 |
1 |
4145 |
17181025 |
7,122E+10 |
1689 |
1,42E+03 |
1 |
4482 |
20088324 |
9,004E+10 |
1020 |
1,50E+03 |
1 |
5611 |
31483321 |
1,767E+11 |
1144 |
1,75E+03 |
1 |
5862 |
34363044 |
2,014E+11 |
5107 |
1,81E+03 |
1 |
5889 |
34680321 |
2,042E+11 |
704 |
1,81E+03 |
1 |
6920 |
47886400 |
3,314E+11 |
1125 |
2,03E+03 |
1 |
6986 |
48804196 |
3,409E+11 |
2687 |
2,04E+03 |
1 |
7028 |
49392784 |
3,471E+11 |
2058 |
2,05E+03 |
1 |
7117 |
50651689 |
3,605E+11 |
3358 |
2,07E+03 |
1 |
7445 |
55428025 |
4,127E+11 |
4613 |
2,14E+03 |
1 |
7643 |
58415449 |
4,465E+11 |
1880 |
2,18E+03 |
1 |
7687 |
59089969 |
4,542E+11 |
1490 |
2,19E+03 |
1 |
8500 |
72250000 |
6,141E+11 |
1763 |
2,36E+03 |
1 |
9332 |
87086224 |
8,127E+11 |
2922 |
2,53E+03 |
1 |
9364 |
87684496 |
8,211E+11 |
1606 |
2,54E+03 |
1 |
9747 |
95004009 |
9,26E+11 |
1364 |
2,62E+03 |
1 |
10075 |
1,02E+08 |
1,023E+12 |
1527 |
2,69E+03 |
1 |
10262 |
1,05E+08 |
1,081E+12 |
2174 |
2,74E+03 |
1 |
12107 |
1,47E+08 |
1,775E+12 |
1770 |
3,17E+03 |
1 |
14272 |
2,04E+08 |
2,907E+12 |
5768 |
3,76E+03 |
1 |
15460 |
2,39E+08 |
3,695E+12 |
5067 |
4,15E+03 |
1 |
19771 |
3,91E+08 |
7,728E+12 |
5497 |
6,04E+03 |
По формуле находим В =
.
Получаем уравнение:
ŷ = 211,367 + 0,355 * х –
1,879Е–05 * х2 + 7,969E-10 * x3. Построим
график – геометрическую интерпретацию
модели:
