Расчет методом баланса работ без учета работ среза на границах опд.
Калибрующий участок Рис. 5а.
Пусть, часть
заготовки находящаяся в калибрующем
участке, переместилась по направлению
скорости деформирования
на
.
Тогда
АВ=
, гдеUz
– перемещение пуансона;
АПл.Д.=0; т.к. эта часть заготовки пластически не деформируется.
Подставляя АВ и АПл.Д. в (1), получим:
=0
и
.
Приняв:
окончательно получим:
,
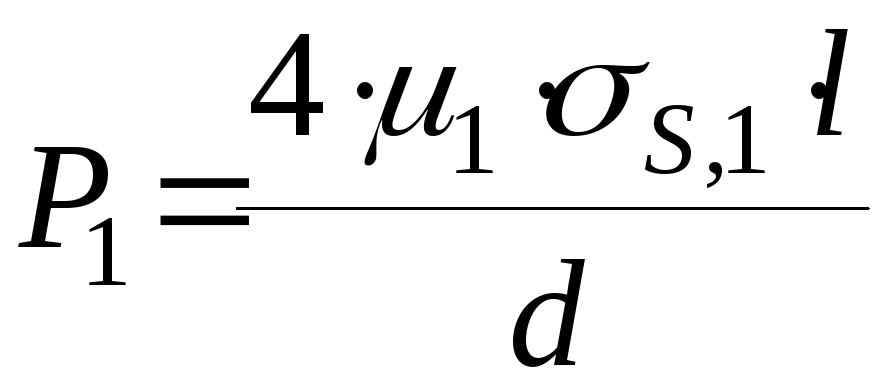(2)
где l-
длина калибрующего участка,
-
напряжение течения металла в калибрующем
участке.
Конический участок.
Тот же метод, но с использованием сферической системы координат и следующих допущений:
за верхнюю границу ОПД принимается поверхность части сферы радиуса b (см. рис.5, б) с углом при вершине конуса 2γ;
за нижнюю границу ОПД принимается поверхность части сферы радиуса a (см. рис. 5, б) с углом при вершине конуса 2γ;
перемещения частиц в ОПД происходят по радиусам ρ, функция Uρ зависит только от ρ и не зависит от φ и θ.
Функцию Uρ получим из равенства мгновенных расходов через соответствующие поперечные сечения матрицы. Пусть частицы вблизи верхней границы ОПД переместились на Uz, как и пуансон, тогда расходы через поверхности, определяемые радиусами b и ρ, запишутся как:
,
(3)
но
. (4)
Подставляя (4) в (3) для Uρ, получим:
.
(5)
Для расчета работы пластической деформации потребуются компоненты:
ξρ, ξθ, и ξφ причем ξθ,=ξφ.
.
(6)
Условие несжимаемости ξρ+ξθ,+ξφ=0 выполняется.
Находим ξi=
,
пренебрегая γρz
.
АПл.Д.=
,
где σs,2
– среднее по ОПД значение напряжения
течения металла, выбранное по средним
значениям:
,
,
и θ.
dV=2
Окончательно:
.
Можно показать,
что 
.
, где
,
f–
площадь поверхности трения;
.
.
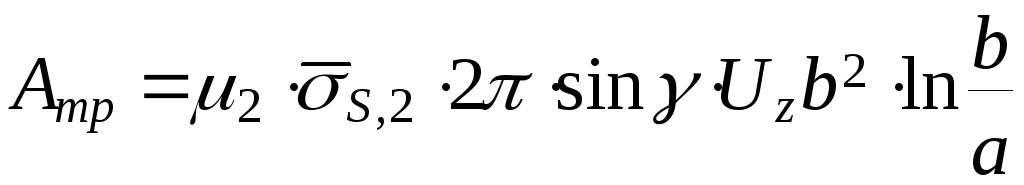Подставляя в (1), получим
и для р2:
,
-
среднее значение напряжения течения
металла в ОПД.
Контейнер:
.
АПл.Д.=0;
Получаем: 
,
гдер3
– удельная сила деформирования, L-
длина контейнера,
-
напряжение течения металла в калибрующем
участке.
Сила деформирования:
.
(7)
Для построения графика технологических нагрузок используют типовой (если нет других методов, позволяющих моделировать выдавливание на неустановившейся стадии) график. См. рис.7, рис.8.
Банкетов и др. КШО 1970г. Стр 343.
Горячее выдавливание:
,
где
-рабочий
ход.
Холодное выдавливание:
Величину рабочего хода можно приближенно оценить по выражению:
=lст+S1,
где l
– длина стержневой части заготовки
после выдавливания, S1
– ход пуансона, соответствующий
заполнению воронки матрицы (Рис. 9).
1 – исходная цилиндрическая заготовка;
2 – заготовка (отмечено пунктиром), соответствующая заполнению воронки матрицы металлом;
3 – заготовка после выдавливания.
Силу деформирования для установившейся стадии процесса рассчитывают по формуле (7).
Продольное выдавливание с перемещением материала заготовки от центра к периферии и ограничением ОПД инструментом (обратное выдавливание).
Книга: Сопротивление материалов пластическому деформированию в приложениях к процессам обработки металлов давлением. Под. Ред. А.В. Лясникова. Санкт-Петербург 1995 г. 527с. с ил.
по
(ξi) 
h – глубина полостти.
r
– радиус пуансона.
.
f – коэффициент трения по Куллону.
Продольное выдавливание с перемещением материала заготовки от периферии к центру и ограничением ОПД инструментом.
Холодное выдавливание
;
=
(ξi);
hм – высота калибрующего участка.
.
(8)
2φм – угол матрицы.
Поперечное выдавливание с перемещением материала сплошной заготовки от центра к периферии.
=
(ξi).
.
.
е=2,71 – основание натурального логарифма.
b=1,08.
f – коэффициент трения по закону Куллона.
σТ – начальное напряжение течения при ξi=0.002.
hк – по формуле (8).
Поперечное выдавливание с перемещением материала полой заготовки от периферии к центру, стр.337 – 338.