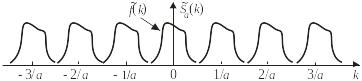
Дельта-функция в трехмерном пространстве
Декартовы
координаты:
,
.
.
(2.44)
Интегральное представление
.
(2.45)
Сферические
координаты:
,
,
,
,
,
,
,
,
(2.46)
,
,
,
.
В
случае центральной
симметрии
,
тогда
.
Нормировка
,
с учетом
,
,
дает
,
.
(2.50)
Гребенчатая функция
(2.53)
Моделирует неограниченную кристаллическую решетку, антенну и другие периодические структуры.
При Фурье-преобразовании гребенчатая функция переходит в гребенчатую функцию.
Из (2.53)
,
с учетом
(2.8)
получаем
.
(2.54)
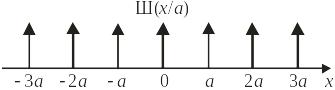
Свойства
Функция четная
,
периодическая
,
период
.
Фильтрующее свойство дельта-функций
дает
.
(2.55)
Фурье-образ
Для
периодической функции
с периодом L
Фурье-образ
выражается через коэффициенты Фурье
,
(1.47)
,
(1.49)
Для гребенчатой функции с периодом получаем
,
где учтено фильтрующее свойство дельта-функции. Из (1.47) находим Фурье-образ
.
(2.56)
Фурье-образом гребенчатой функции является гребенчатая функция.
Из (2.56) по теореме Фурье о масштабном преобразовании аргумента получаем
.
(2.59)
Увеличение
периода гребенчатой функции
(
)
уменьшает период и увеличивает амплитуду
ее спектра.
Ряд Фурье
Используем
,
(1.48)
.
Для
,
получаем
.
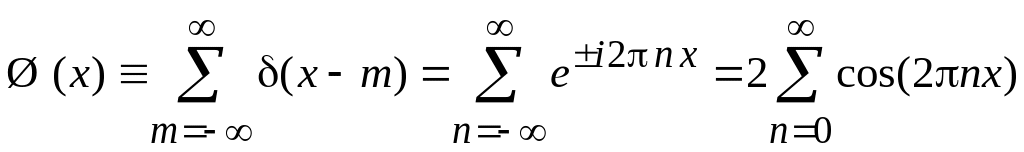(2.57)
Формула суммирования Пуассона
.
(2.60)
Сумма значений функции в целочисленных точках равна сумме значений ее спектра в целочисленных точках, если ряды существуют.
Доказательство:
Выражение
(2.57)
подставляем
в интеграл
и с учетом фильтрующего свойства
дельта-функции получаем
.
Обобщенная формула суммирования Пуассона
,
(2.61)
Доказательство:
Выражение
,
(2.57)
подставляем
в интеграл
.
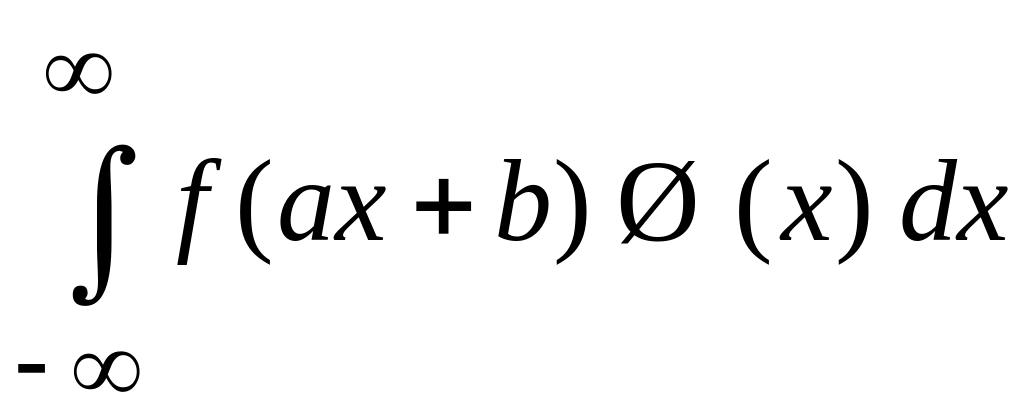Для левой и правой частей (2.57) получаем
левую и правую части (2.61)
,
.
Аналогично доказывается обратная формула суммирования
.
(2.61а)
Произведение гребенчатой и гладкой функций
Подставляем гребенчатую функцию с периодом a
, (2.54)
используем фильтрующее свойство дельта-функции
,
(2.3)
получаем
.
(2.67)
Произведение гребенчатой и гладкой функций дает модулированную гребенчатую функцию.
Фурье-образ
Используем (2.67) и фильтрующее свойство дельта-функции
.
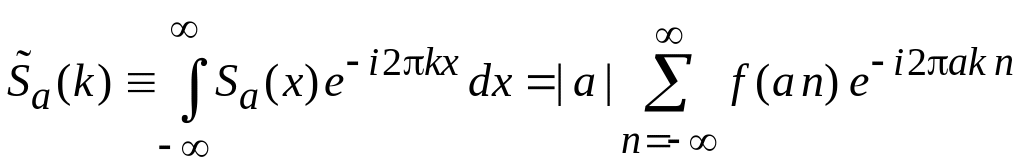(2.68)
В формуле суммирования Пуассона (2.61а)
заменяем
,
и находим
.
(2.61б)
Сравнение (2.68) и (2.61б) дает
.
(2.68)
Спектр
произведения гребенчатой функции с
периодом a
и гладкой функции является суммой
спектров гладкой функции, сдвигаемых
на целое число шагов
.
Для
ограниченно
определенной функции
спектр
имеет ширину, гораздо меньшую
.
Тогда для
спектр
является периодическим повторением
спектра
с периодом
.
