
Hauslekture. Методическое пособие - Ситникова О.А., Галкина О.В
..pdfBeispiel dafür sind Programme zur Steuerung von Produktionsanlagen, die fast immer nur für eine konkrete Anlage erstellt werden müsssen und entsprechend teuer sind.
Hier nun die verschiedenen Programme im Oberblick:
8. Standardanwendungen
Textverarbeitung: Textvearbeitung ist eine der häufigsten Anwendungen eines Rechners. Für spezielle Fälle gibt es spezielle Text Verarbeitungen, die sich untereinander im Detail und Funktionsumfang unterscheiden. Für einfache Anwendungen verwendet man einen Editor, der nur geringe Text Verarbeitungsfunktionen besitzt. Ein Editor dient im wesentlichen zur Eingabe von Programmen, die zeilenweise aufgebaut sind. Ein solcher Editor bietet Funktionen zum Einrücken von Textteilen, zum Suchen und Ersetzen von Texten sowie zum Speichern und Laden von Textblöcken.
Wenn das Aussehen eines Textes wichtig ist, reicht ein Editor nicht mehr aus. Man braucht zusätzliche Funktionen, die für Randausgleich sorgen oder für verschiedene Schriftarten. Auch automatische Inhaltsverzeichnisse und die Einbindung von Grafiken wird gewünscht. Diese Textverarbeitungsprogramme (z.B. Word, WordStar oder WordPerfect) sind häufig in der Bürowelt anzutreffen. Ihnen gemeinsam ist, daß man auf dem Bildschirm genau das sieht, was auch später auf dem Papier steht.
Einen anderen Weg gehen die sogenannten Textprozessoren. Hier wird der Text mit einem normalen Editor erstellt und durch eingestreute Kommandos für den Druck aufbereitet. Das Ergebnis sieht man dann erst später auf dem Papier. Der Vorteil dieses Verfahrens ist, das der Autor des Textes nicht durch das Layout und die Gestaltungsmöglichkeiten eines Textverarbeitungssystems abgelenkt wird. Der bekannteste Vertreter dieser Gruppe ist TßX, das es für fast alle Rechnertypen gibt und auch in vielen Druckereien und Verlagen verwendet wird. Übrigens wurde auch dieses Skript damit erstellt.
Datenbanksysteme: Ein Datenbanksystem ist wie ein Karteikasten auf elektronische Art. Die Karteikarte nennt man Datensatz und die einzelnen Zeilen heißen Felder. Das Datenbanksystem übernimmt die Organisation der Datensätze, indem es das schnelle Suchen und Sortieren übernimmt.
Über Abfragesprachen kann man Informationen aus den Datensätzen extrahieren und zu neuen Datensätzen zusammenfügen. Alle Funktionen sind bequem über Funktionstasten und Menüs zu erreichen. Die bekanntesten Vertreter dieser Gruppe sind dBase, Oracle und Ingres.
Graflkprogramme: Grafiken dienen zur besseren Darstellung abstrakter Zusammenhänge. Am bekanntesten sind die Grafiken aus der Wahlberichtserstattung der Fernsehanstalten. Solche Geschäftsgrafiken in Form von Balkenoder Tortendiagrammen sollen große Datenmengen anschaulich machen. Solche Datenmengen fallen vor allem bei Datenbanksystem an, so daß die meisten Grafikprogramme in der Lage sind, auf die Daten der gängigsten Datenbanksysteme
41
zurückzugreifen. Typischer Vertreter dieser Gruppe sind Harvard Graphics und MS-Chart.
Malprogramme: Ein Malprogramm ist für den künstlerisch ambitionierten Computeranwender gedacht. Es vertauscht den Zeichenblock mit dem Bildschirm und den Bleistift mit der Maus. Neuere Malprogramme sind in der Lage echte Bilder, die über einen Scanner in den Rechner eingelesen wurden, weiter zu verarbeiten und zu manipulieren.
Dazu stehen Funkionen zum freihändigen Zeichen, zum schnellen Erzeugen verschiedener geometrischer Figuren und zum Einfärben zur Verfügung. Bekannte Beispiele sind MS-Paint und PC-Paintbrush.
CAD-System: Das CAD-System' dient dem Konstrukteur oder Technischen Zeichner als Ersatz für das Zeichenbrett. Ein CAD-System ähnelt einen Malprogramm, das für professionelle Ansprüche aufgebohrt wurde. Alle Funktionen eines Malprogrammes finden sich auch hier. Darüber hinaus finden sich auch Funktionen zum Bemaßen der konstruierten Teile, Stücklistengeneratoren und Normteil-Bibliotheken. Der auf den ersten Blick nicht sichtbare Unterschied liegt in dem grundsätzlich anderen Aufbau der Zeichnung im CAD-System und im Malprogramm. Während im Malprogramm jedes Objekt durch eine endliche Anzahl von Punkten (Pixel) dargestellt wird, verwendet das CAD-System eine mathematische Beschreibung (Vektor) zur Beschreibung der Objekte. Dadurch ist eine dünne Linie auch bei beliebiger Vergrößerung noch immer eine dünne Linie. Nachteil ist der immense Rechenaufwand, den dieses Verfahren verlangt. Ein CAD-System bleibt daher dem professionellem Einsatz vorbehalten. Das bekannteste Produkt für den PCBereich ist AutoCAD.
Tabellenkalkulationsprogramme: Für immerwiederkehrende Berechnungen vieler voneinander abhängiger Werte dienen Tabellenkalkulationsprogramme. Sie stellen eine Kombination aus Textverarbeitung und Datenbank dar. Wie in einer Tabelle auf Papier kann man in Zeilen und Spalten seine Rechenaufgaben erledigen. Der Computer erledigt dabei die Neuberechnung des gesamten Blattes in Sekundenbruchteilen. Die Abhängigkeiten zwischen den einzelnen Feldern werden durch (mathematische) Formeln beschrieben. Durch Änderung einiger Feldwerte kann man sehr schnell Prognosen und Simulationen erhalten. Hauptanwendungsgebiete der Tabellenkalkulationsprogramme sind daher das betriebliche Rechnungswesen und die Auswertung von statistischem Material. Das zur Zeit bekannteste Produkt ist MSExcel.
Integrierte Anwendungen: Die integrierten Anwendungen erledigen mehrere der bisher genannten Aufgabe unter einem Dach, sprich einem Programmpaket. Sie enthalten Textverarbeitung, Datenbank, Tabellenkalkulation und Grafikteil. Durch die gemeinsame Umgebung ist es leicht möglich, die Ergebnisse aus verschiedenen Teilen zu einem Gesamtwerk (z.B. einem Text mit Grafik und Tabellen) zusammenzustellen. Manche Produkte enthalten daruberhinaus noch weitere Teilfunktionen, z.B. eine Möglichkeit zur Kommunikation mit einem anderen Rechner. Die bekanntesten Produkte sind FrameWork, MS-Works und OpenAccess.
42
9. Dienstprogramme
Dienstprogramme (oder Utilities) sind für den Betrieb eines Rechners unerläßlich. Bei Großrechnern gehören sie zum Lieferumfang der Anlage. Dort dienen sie zum Steuern des Rechners selbst, der Benutzerund Programmverwaltung. So gibt es Dienstprogramme für das Neueintragen eines Anwenders, für das Anlegen von Sicherungsdateien oder für die Verwaltung der zentralen Drucker.
Im PC-Bereich sieht die Situation anders aus. Hier ist der Anwender gleichzeitig auch Maschinenbediener. Der Rechner steht dem Anwender vollständig zur Verfügung. Das Betriebssystem ist nicht direkt Bestandteil des PC's sondern wird von einem anderen Hersteller bezogen. Im Gegensatz zu einem Großrechner gibt es für den PC verschiedene Betriebssysteme für unterschiedliche Anforderungen. Der Funktionsumfang des PC-Betriebssystems ist entsprechend eingeschränkt. Diese Lücke wird durch die Hersteller von Utility-Programmen geschlossen. Beispiele für Betriebssysteme sind MS-DOS und DR-DOS, die bekanntesten Utilities sind die Norton-Utilities und PC-Tools. Dem Trend zu immer einfacherer Programmierung folgend, gehen immer mehr Hersteller dazu über, ihre Programme in ein bedienerfreundliches Kleid zu packen. Dieses Kleid nennt man Oberfläche oder im besonderen dann grafische Oberfläche. Dann kann man die komplette Bedienung eines Programms mit der Maus und über Menüs erledigen. Bestes Beispiel dafür ist das Programm Windows, das heute beim Kauf eines Rechners schon mitgeliefert wird.
Compiler/Übersetzer dienen zur Erstellung eigener Programme. Ein Programm wird in einer Hochsprache geschrieben und dann vom Compiler in maschinenverständliche Befehle übersetzt.
Die Wahl der Hochsprache ist zum einen Geschmackssache, zum anderen eine inhaltliche Entscheidung. Eine universelle Programmiersprache für alle Zwecke gibt es nicht. So gibt es Sprachen für finanzwirtschaftliche Problemstellungen (Cobol), Sprachen für systemnahe Programme (C) oder Sprachen, die besonders gut für Lehrzwecke geeignet sind (Pascal, Modula-2)
10. Der Algorithmus, das unbekannte Wesen
Um den Algorithmus dreht sich in einer Programmieraufgabe immer alles. Er ist der Schlüssel zur Lösung des Problems. Hat man den Algorithmus, ist jedes Problem so gut wie gelöst! Das Umgekehrte gilt natürlich auch. Aber damit wissen wir immer noch nicht, was ein Algorithmus ist.
Unter Algorithmus versteht man ein Verfahren, das in einer endlichen Zahl von Schritten zu einem definierten Ergebnis kommt. Dieser Vorgang muß bei unveränderten Anfangsbedingungen immer wieder zu den selben Endzuständen führen. Diese Eigenschaften nennt man deterministisch und reproduzierbar. Klingt alles sehr kompliziert, ist aber genauso einfach wie Kuchen backen. Und dieser Vergleich hinkt kein bißchen! Wer ein Rezeptbuch aufschlägt, findet dort nämlich lauter Algorithmen aufgeschrieben. Mit anderen Worten, ein Algorithmus ist ein Kochrezept!
43
Nun gibt es für ein und dasselbe Menü verschiedene Rezepte, und mit Algorithmen ist es ebenso. Nehmen wir zum Beispiel das folgendes Problem:
Ein Kunde bezahlt an der Kasse mit einem 100 DM Schein. Seine Rechnung beträgt aber nur 47,11 DM. Wie soll der Differenzbetrag zurückgegeben werden?
Im ersten Moment sagt jeder, das Rückgeld von 52,89 DM setzt sich zusammen aus einem 50 DM Schein, einem 2 DM Stück, einem 50 Pf Stück, drei 10 Pf Stücken, einem 5 Pf Stück und zwei 2 Pf Stücken.
Das ist sicher eine Möglichkeit, das Geld zurückzugeben. Aber wie kommt man auf genau diese Stückelung? Genausogut hätte man auch 5289 Pfennige zurückgeben können (wenn man mal von den Transportproblemen absieht).
Beginnen wir mit dem Algorithmus für das Verfahren 5289 Pfennige. Er lautet:
1.Ermittle den Rückgabebetrag durch Subtraktion des Rechnungsbetrages vom erhaltenen Betrag.
2.Rechne den erhaltenen Rückgabebetrag in Pfennige um.
3.Gib diese Menge Pfennige zurück.
Und wie sieht das Rezept für das als normal gewohnte Verfahren aus?
1.Ermittle den Rückgabebetrag durch Subtraktion des Rechnungsbetrages vom erhaltenem Betrag.
2.Suche den höchsten, der als Schein/Münze im Rückgabebetrag enthalten ist (kleiner gleich).
3.Reduziere den Rückgabebetrag um diesen Betrag und gib den Betrag zurück.
4.Wiederhole ab Schritt 2 mit dem verbleibenden Rückgabebetrag, bis kein Rückgabebetrag mehr da ist.
Bis hierher haben wir zwei Verfahren zur Lösung desselben Problems kennengelernt. Aus eigener Erfahrung weiß aber jeder, daß weder das eine noch das andere in Reinkultur verwendet wird. Denn unser Algorithmus berücksichtigt besondere Fälle überhaupt nicht. Was wäre denn, wenn in der Kasse gar kein 50 DM Schein ist? Hier würde unser zweiter Algorithmus auf den Bauch fallen, er geht vom Vorhandensein jeder Stückelung aus.
Fügen wir einen zusätzlichen Punkt in unseren obigen Algorithmus ein, können wir auch dieses Problem lösen:
1. |
Ermittle |
den |
Rückgabebetrag |
durch Subtraktion |
des Rechnungsbe- |
||
trages vom erhaltenem Betrag. |
|
|
|
|
|||
2. |
Suche den höchsten, der als |
Schein/Münze im |
Rückgabebetrag |
ent- |
|||
halten ist (kleiner gleich). |
|
|
|
|
|||
3. |
Ist dieser Wert in der Kasse |
vorhanden, arbeite damit, wenn nicht |
|||||
nimm den nächstkleineren, verfügbaren Wert zum Weiterarbeiten. |
|
||||||
4. |
Reduziere |
den |
Rückgabebetrag |
um |
diesen Betrag |
und gib den Betrag |
|
zurück. |
|
|
|
|
|
|
|
5. |
Wiederhole ab |
Schritt 2 mit |
dem |
verbleibenden |
Rückgabebetrag, |
bis |
|
kein Rückgabebetrag mehr da ist.
Dieses letzte Verfahren deckt alle Fälle bei der Geldrückgabe ab, darüberhinaus stellt es auch sicher, daß sowenig Scheine oder Münzen wie möglich den Besitzer
44
wechseln. Man spricht in diesem Zusammenhang auch von einem optimierten Algortihmus.
Übung l Welche Annahme wird im letzten Algorithmus stillschweigend vorrausge-setzt, damit er wirklich funktioniert?
Wie erhält man nun einen (halbwegs) richtigen Algorithmus?
11. Problemzerlegung
Wer ein Problem hat, versucht dies solange wie möglich vor sich herzuschieben. Das ist auch eine Möglichkeit, aber keine Lösung. Der erste Ansatz ist es, das Problem zu verstehen. Weiß man erst einmal, worum es geht, ist schon viel gewonnen.
Hat man das WAS, kann man zum WIE übergehen. Zunächst überlegt man sich, wie man die Aufgabe (oder das Problem allgemein) mit Papier und Bleistift angehen würde. Kommt man auf diese Weise zu einem Ergebnis, ist man fast fertig.
Jetzt gilt es, das soeben per Hand durchexerzierte noch einmal systematisch durchzugehen. Dabei notiert man sich jeden Schritt.
Dieses Rezept muß man jetzt noch einmal auf Ungereimtheiten oder diffuse Anweisungen überprüfen und gegebenenfalls überarbeiten. Man erhält eine Arbeitsanweisung, die auch von einem anderen verstanden werden sollte.
Diese Arbeitsanleitung ist der fertige Algorithmus!
12. Grundstrukturen
Wenn man einige Algorithmen erstellt hat, merkt man sehr schnell, daß sie sich immer wieder aus denselben Grundelementen zusammensetzten. Und es gibt gar nicht so viele davon, sondern nur Drei oder Vier!
Anweisungsfolge: Eine Anweisungsfolge ist eine gewisse Anzahl von Anweisungen, die eine nach der anderen ohne Zögern und Rückfragen durchgeführt werden. Aus dem Geldwechsel-Beispiel kennen wir das noch: Berechne den Rückgabebetrag, Suche den größten darin enthaltenen Einzelwert, Subtrahiere, ...
Eine Anweisungsfolge wird immer vollständig in unveränderlicher Reihenfolge abgearbeitet. Keine Anweisung wird übersprungen oder mehrfach ausgeführt.
Alternative: Eine Alternative im Algorithmus erkennt man an den magischen Worten WENN und DANN. Hier hat das Verfahren dann zwei Möglichkeiten, weiterzumachen. Ein beliebtes Beispiel dafür ist die Bildung des Betrages einer reellen Zahl. Wie man aus der Mathematik-Vorlesung hoffentlich noch weiß, ist der Betrag einer reellen Zahl immer positiv, d.h. ein eventuell vorhandenes Minuszeichen wird einfach weggelassen. Aber wie berechnet man aus einer Zahl irgendwo in den Tiefen des Hauptspeichers den Absolutwert?
Nun, man sieht nach, ob der Betrag der Zahl positiv ist, dann ist alles in Ordnung und man läßt die Zahl wie sie ist. Ist die Zahl dagegen negativ, wird sie mit -1 multipliziert und mit dem neuen Wert weitergearbeitet. Streng formalisiert kann man auch schreiben:
45
WENN der Wert der Zahl kleiner Null ist, DANN multipliziere sie mit -l, SONST lasse den Wert unverändert.
Hier sehen wir auch gleich eine Besonderheit der Alternative, ein Zweig ist leer (1азяе den Wert unverändert bedeutet ja nichts anderes als tue nichts). Das hat aber keinen Einfluß auf die universelle Verwendbarkeit der Alternative im Algorithmus.
Wiederholungen: Auch eine Wiederholung haben wir in unserem GeldwechselBeispiel schon gehabt. Dort stand: ... wiederhole bis kein Rückgabebetrag mehr da ist.
Die magischen Worte hier sind WIEDERHOLE und BIS. Eine andere beliebte Kombination besteht aus SOLANGE und WIE. Aber was kann man wiederholen? Nun, einfach alles! Innerhalb einer Wiederholung (dem sogenannten Schleifenkörper) sind beliebige (!) Anweisungen erlaubt. Dieser Satz ist leicht dahin geschrieben, aber so fundamental, das er später noch näher betrachtet wird.
Bilder sagen bekanntlich mehr als tausend Worte, und daher haben sich einige kluge Köpfe eine graphische Darstellungsart ausgedacht. Gebräuchlich sind verschiedene Methoden, uns interessieren hier nur die sogenannten Struktogramme, die nach ihren Erfindern auch Nassi-Shneiderman-Diagramme genannt werden. Die hier gezeigten Elemente sind nicht vollständig, es fehlen noch einige wenige Spezialfälle, die an der entsprechenden Stelle nachgereicht werden.
Nun zu den Struktogrammen im allgemeinen und den verschiedenen Elementen im besonderen. Jedes Struktogramm setzt sich nur aus einer beliebigen (!) Anordnung von Einzelelementen zusammmen. Dabei heißt beliebig, daß die folgenden Regeln eingehalten werden:
•Jedes Struktogramm hat genau einen Eingang und einen Ausgang.
•Die Breite eines Struktogrammes bleibt über die gesamte Höhe konstant.
•Alle Grundelemente sind rechteckig, aber in der Größe variabel.
•Um die Übersichtlichkeit zu erhöhen, können Teile eines Struktogramms ausgelagert und getrennt weitergeführt werden.
•Jedes Struktogramm (bzw. Teilstruktogramm) trägt einen eindeutigen Titel.
•in einem Struktogramm werden nur funktionelle Abläufe dargestellt.
Nun zu den Elementen im einzelnen. Der einfachste Fall ist die Anweisungsfolge. Die Anweisungen werden der Reihe nach von oben nach unten abgearbeitet. Keine Anweisung wird mehrfach ausgeführt oder übergangen. In das Feld wird mit normaler deutscher Sprache die Anweisung eingetragen. Fast alle Probleme in der EDV lassen sich auf eine Folge von drei Anweisungen (hier besser Anweisungsblöcke) zurückführen, der erste Block heißt Eingabe, der zweite Verarbeitung und der dritte Ausgabe. Nach diesem EVA-Prinzip arbeiten (fast) alle EDV-Programme.
46

|
|
Bedingung |
|
|
Anweisung 1 |
|
|
|
|
|
|
|
|
Ja |
nein |
|
Anweisung 2 |
||
|
|
|
|
|
Anweisung 3 |
Anweisung |
Anweisung |
|
|
||
Anweisungsfolge |
Alternative |
|
|
Wiederholung |
Wiederholung |
|
|
|
Bedingung |
Anweisung (en) |
|
|
Anweisung (en) |
Bedingung |
|
Die Alternative ermöglicht uns, Verzweigungen in den starren Ablauf der Anweisungsfolge einzubauen. Das auf der Spitze stehende Dreieck nimmt die Bedingung auf, die zur Entscheidung führen soll. Aus unserem Geldwechselbeispiel auf Seite 18 wissen wir noch ... ist dieser Wert vorhanden, arbeite damit, wenn nicht nimm den nächstkleineren... Hier gibt es zwei Möglichkeiten für das Weiterarbeiten, entweder ist der Wert vorhanden oder er ist nicht vorhanden. Nach der Aufteilung wird aber dann an einer gemeinsamen Stelle im Ablauf weitergemacht.
Links und rechts unterhalb des Bedingungs-Dreiecks werden die beiden möglichen Ergebnisse der Entscheidung eingetragen. Im einfachsten Fall ist dies Ja oder Nein, denkbar sind aber auch andere Begriffe. Einen Sonderfall stellt die Alternative mit einem leeren Zweig dar. Man spricht dann auch von einer bedingten Anweisung. Um deutlich zu machen, daß man den zweiten Zweig nicht aus Versehen leer gelassen hat, wird dieser dann mit einem Prozentzeichen (%) markiert.
Durch die Wiederholung wird eine Anweisungsfolge mehrfach durchgeführt. Man unterscheidet zwei Arten von Wiederholungen, zum einen die kopfgesteuerte Schleife, zum anderen die fußgesteuerte Schleife. Der kleine, aber feine Unterschied liegt im Detailablauf. Die kopfgesteuerte Schleife (auf Seite 21 links unten) prüft gleich zu Anfang, ob die Bedingung für die Ausführung des Schleifenkörpers erfüllt ist. Wenn ja, wird der Schleifenkörper solange durchgeführt, bis die Bedingung nicht mehr gültig ist. Es kann also durchaus passieren, daß die Bedingung schon von Beginn an nicht erfüllt ist und der Schleifenkörper niemals durchgeführt wird. Man nennt diese Schleifenart daher auch abweisende Schleife.
47
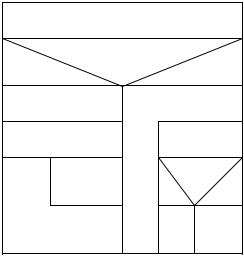
Anweisung 1
Bedingung 1 ja nein
Anweisung 2 Bedingung 3
Anweisung 3 |
Anw. 5 |
|
|
Bed. 4 |
|
Anw. 4 |
j |
n |
Bedingung 2 |
A 6 |
A 7 |
Etwas anders verhält es sich bei der fußgesteuerten Schleife. Hier wird der Schleifenkörper in jedem Fall mindestens einmal durchlaufen, erst dann wird die Bedingung am Ende überprüft. Je nach Ergebnis dieser Prüfung wird der Schleifenkörper dann wiederholt. Diese Schleife nennt man wegen ihrer freundliche Gesinnung daher auch nicht abweisende Schleife.
Und wie oft wird so eine Schleife (welcher Art auch immer) nun durchlaufen? Das ist einzig und allein Sache des Programmierers oder Entwerfers. Die Abbruchbedingung steht zwar fest, aber das Erreichen dieser Bedingung liegt völlig in der Hand des Programmierers. So kommt es sehr oft vor, daß der Schleifenkörper bis zum Erreichen eines bestimmten Zählerstandes durchgeführt werden soll. Vergißt man aber, den Zähler zu erhöhen, dann wird das Programm bis zum ewigen Ende laufen, da ja die Abbruchbedingung nie erreicht werden kann!
Damit das nicht zu häufig passiert, gibt es einen Sonderfall der abweisenden (=kopf-gesteuerten) Schleife. Kennt man die Anzahl der Wiederholungen schon vor Eintritt in die Schleife, kann man die Zählschleife verwenden, die sich von der normalen, abweisenden Schleife nur dadurch unterscheidet, daß die Verwaltung (=Erhöhen oder Erniedrigen) des Zählers automatisch erfolgt. Das Struktogramm unterscheidet nicht zwischen abweisender Schleife und Zählschleife!
Damit haben wir die Grundelemente jedes Algorithmus kennengelernt. Es folgen nun einige Übungen zur Umsetzung eines Problems in einen Algorithmus und Struktogramm.
Übung 2 Es soll ein Programm zur Umrechnung von km/h in m/s erstellt werden. Wie sieht das zugehörige Struktogramm aus?
48
Übung 3 Wie sieht das Struktogramm zum Geldwechsel-Beispiel auf Seite 18
aus?
Übung 4 Ein Programm soll entscheiden, ob zwei eingegebene Zahlen positiv sind.Wie sieht das Struktogramm aus?
Übung 5 Der Computer jlenkt" sich eine Zahl aus. Der Anwender gibt eine Zahl ein und erhält als Anwort entweder zu hoch, zu niederig oder richtig. Wie sieht das Struktogramm aus?
Soweit das Kapitel zum theoretischen Vorgehen. Die wesentliche Erkenntnis sollte sein, daß man ein Problem durch schrittweise Verfeinerung in immer kleinere Teilprobleme aufgliedert. Das Ergebnis sollte ein Struktogramm sein, das sich dann leicht in eine Programmiersprache umsetzten läßt. Man kann sich grundsätzlich merken, daß man alles, was man im Struktogramm legal zeichnen kann, auch ohne Krücken und Hintertürchen programmieren kann. Wie das geht, sehen wir im folgenden Kapitel.
13.Auch Programme sind nur Menschen
Jetzt wird es ernst. Bisher haben wir uns mehr oder weniger frei im künstlerischen Bereich mit dem Malen von Struktogrammen beschäftigt. Wir wissen jetzt (hoffentlich), wie man aus einem Problem einen Algorithmus entwickelt und daraus ein korrektes Struktogramm. Bisher kam die Programmiersprache überhaupt noch nicht vor, und das war auch Absicht. Nun aber geht es ans Eingemachte. Für die EDV-Grundausbildung bietet sich die Sprache Pascal an, da sie alle Forderungen an eine strukturierte Programmiersprache erfüllt.
14. Aufbau eines Pascal-Programms
Jedes Pascal-Programm besteht aus drei Teilen. Es beginnt mit dem Programmkopf, dann kommt der Deklarationsteil und zum Schluß der Anweisungsteil.
Mit dem was wir bisher wissen, könnte man ganz zu recht annehmen, daß im Anwei-sungsteil die Anweisungen stehen. Aber was sind dann Programmkopf und Deklarationsteil?
Nun, der Programmkopf entspricht der Überschrift im Struktogramm. Er gibt dem Kind (Programm) einen Namen. Das ist die geringste Arbeit überhaupt, denn man kommt mit einer einzigen Zeile aus: PROGRAM programmname;
An dieser Zeile können wir auch gleich die Notation für den nachfolgenden Text erläutern. In SCHREIBMASCHIHESSCHRIFT werden die sogenannten Pascal- Schlüssel-worte angegeben. Schlüsselworte sind die Worte, die genau so und nicht anders geschrieben werden müssen. Sie haben innerhalb der Sprache Pascal eine
49
bestimmte Bedeutung (eben eine Schlüsselbedeutung). Insgesamt gibt es 35 dieser Schlüsselworte, die wir im Laufe dieses Kapitels kennenlernen werden.
Kursive Textteile kennzeichnen Namen und Bezeichnungen, die durch den Programmierer (im Rahmen gewisser Spielregeln) frei gewählt werden können.
Darüberhinaus gibt es noch Zwitter, die in „normaler" Schrift erscheinen. Dabei handelt es sich um Namen von Prozeduren oder Funktionen (was das ist, kommt noch), die zum Lieferumfang, aber nicht zu den Schlüsselworten gehören.
Grundsätzlich gilt: Pascal macht keinen Unterschied zwischen Großund Kleinschreibung. Es ist also egal, ob man PROGRAM oder program oder auch pRoGrAm schreibt. Wie man aber schon hier sieht, hat die unterschiedliche Schreibweise enormen Einfluß auf die Lesbarkeit eines Programms. Und damit auch jemand, der das Programm beim Entstehen nicht jede Sekunde vor Augen hatte, sofort weiß, was abgeht, gelten folgende Konventionen:
•Pascal-Schlüsselworte werden durchgängig groß geschrieben.
•Vom Programmierer vergebene Namen und Bezeichner werden durchgängig klein geschrieben.
•Bei Standardfunktionen wird nur der erste Buchstabe groß geschrieben.
15. Der Deklarationsteil
Der Deklarationsteil hat zwei Funktionen. Zum einen erklärt er dem Compiler, welche Speicherplätze im Programm benötigt werden, zum anderen gibt er dem Programmierer die Möglichkeit, sich eigene Datenstrukturen (kommt auch noch!) zu basteln.
Fangen wir einfach mal mit dem Begriff Daten an. Daten sind das, womit unser Programm später arbeitet. Unser Algorithmus kümmert sich überhaupt nicht um Daten, er nimmt einfach an, daß sie da sind! Der Rechner ist da etwas penibler. Er will genau wissen, wie die Daten aussehen, mit denen wir arbeiten wollen. Und das schon, bevor auch nur eine einzige Anweisung ausgeführt wurde.
Das hat für den Compiler organisatorische Gründe, er muß für jedes Datum nämlich Speicherplatz reservieren. Den Programmier zwingt er dadurch, sich vorher zu überlegen, was er eigentlich braucht.
16. Grunddatentypen
Nun gibt es verschiedene Sorten Daten, die unterschiedliche Anforderungen an den Speicher stellen. Wie wir im Kapitel 2.1 gesehen haben, werden im Rechner alle Zahlen im Dualsystem dargestellt. Für die Nullen und Einsen steht für eine Zahl eine gewisse Anzahl von Bits (das ist genau eine Dualstelle) zur Verfügung. Üblich sind 16 Bit für eine ganze Zahl. Mit 16 Bit kann man 65536 (=2le) verschiedene Zahlen darstellen. Will man auch noch negative Zahlen haben, reicht das ganze von -32768 bis +32767.
Nun wird sich mancher sagen, das ist schon eine ganze Menge, was will man mehr. Nun, wie wäre es mit einer Zahl zwischen 2 und 3, z.B. 2.5? Mit dem bisher
50
