
- •Содержание
- •1. Содержательная постановка задачи синтеза оптимальных расписаний параллельно-последовательной обслуживающей системы.
- •2. Постановка задачи оптимизации расписаний параллельной системы с задержками поступления заявок
- •3. Редукция задачи оптимизации расписаний параллельной системы в задачу частично-целочисленного линейного программирования
- •4. Бикритериальная упрощенная формулировка задачи синтеза расписаний параллельной системы и алгоритм решения
- •5. Декомпозиционные приближенные алгоритмы оптимизации расписаний параллельной системы с задержками поступления заявок. Жадный алгоритм и бикритериальное приближение.
- •6. Динамическое программирование с отсевом вариантов в оптимизации расписаний параллельной системы с задержками поступления заявок
- •7. Последовательные многостадийные обслуживающие системы. Моделирование на смешанных сетях.
- •8. Модификации метода ветвей и границ оптимизации расписаний последовательных многостадийных обслуживающих систем (jsp)
- •9. Алгоритм неполной декомпозиции задач оптимизации расписаний последовательных обслуживающих систем.
- •10. Многостадийные параллельно-последовательные обслуживающие системы. Подходы к формализации задач управления.
- •11. Декомпозиционный алгоритм оптимизации расписаний многостадийных параллельно-последовательных обслуживающих систем
- •12. Приложение моделей и алгоритмов оптимизации расписаний многостадийных параллельно-последовательных систем.
- •13. Содержательная постановка задачи управления материальными потоками предприятия
- •14. Формальная постановка задачи оптимизации управления входными и выходными материальными потоками
- •15. Задача оптимизации поставок сырья и комплектующих на предприятии. Содержательная постановка.
- •16. Формальная постановка задачи оптимизации поставок
- •17. Определение оптимальных цен продаж в задаче оптимизации управления входными и выходными материальными потоками
- •18. Декомпозиционный алгоритм решения задачи оптимизации поставок
- •19. Программные средства (пс) оптимизации управления входными и выходными материальными потоками предприятия (целиком из монографии)
- •20. Пс оптимизации расписаний последовательных, параллельных и параллельно-последовательных систем
- •21. Имитационное моделирование производственных систем и процессов. Языки, системы им.
- •22. Основные блоки сим Арена и их атрибуты.
- •23. Основные операторы языка gpss.
- •24. Моделирование параллельных систем в сим Арена
- •25. Моделирование последовательных систем в сим Арена.
- •26. Моделирование параллельных систем в gpss world.
- •27 Моделирование последовательных систем в gpss world.
- •28. Среда ibm ilog cplex studio. Назначение, возможности, задачи моделирования, разрешимые и неразрешимые в этой среде.
- •29. Проекты ibm ilog cplex studio, состав, назначение компонент. Основные элементы языка opl.
- •Задача №1.
- •Задача №2. Job Shop
3. Редукция задачи оптимизации расписаний параллельной системы в задачу частично-целочисленного линейного программирования
Приведем (1.1)–(1.8) к нормальному виду задачи математического программирования. Условия (1.5)–(1.8) содержат рекурсивные функции фактических задержек τij. В явном виде τij, как рекурсивные функции относительно переменных xi, j , определяет (1.5). Не раскрыв рекурсии, задачу (1.1)–(1.8) точно решить невозможно. Приведем пример раскрытия рекурсий.
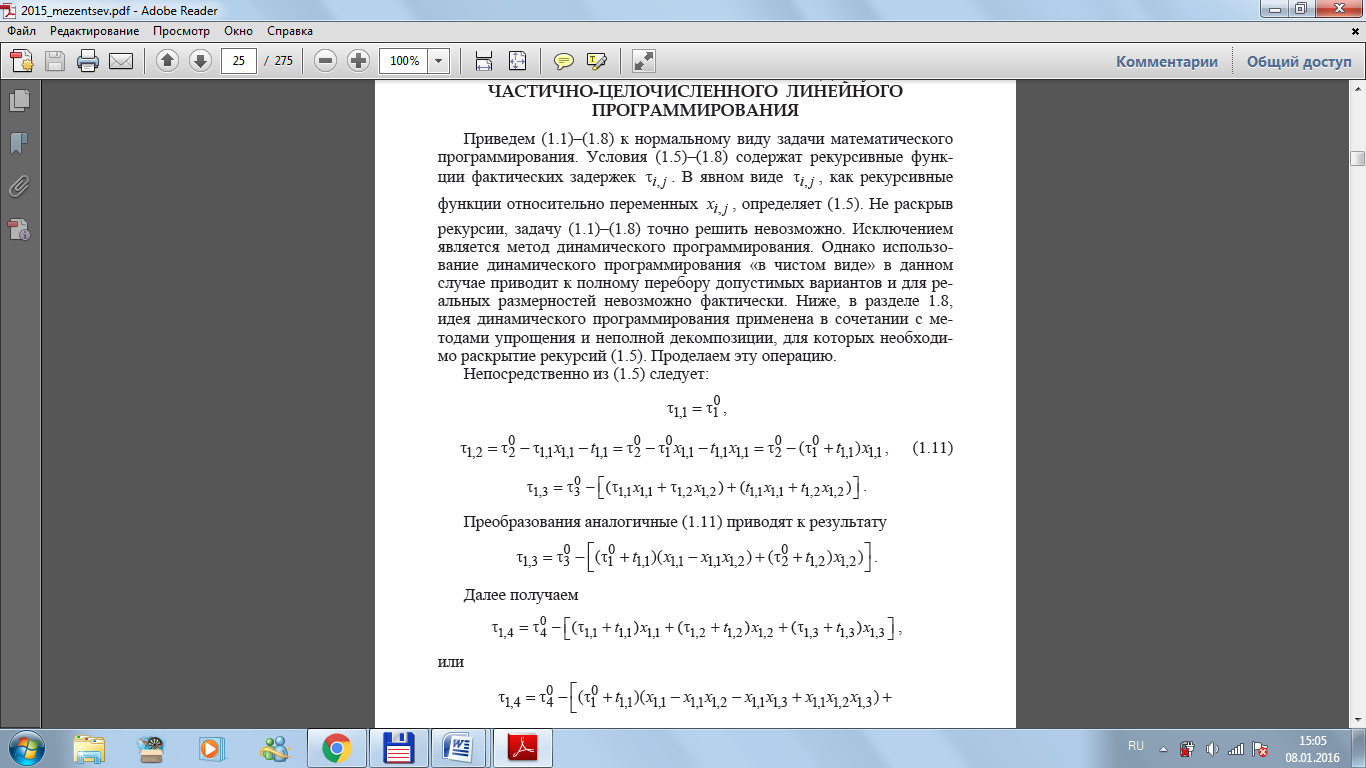
В
1.11
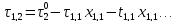

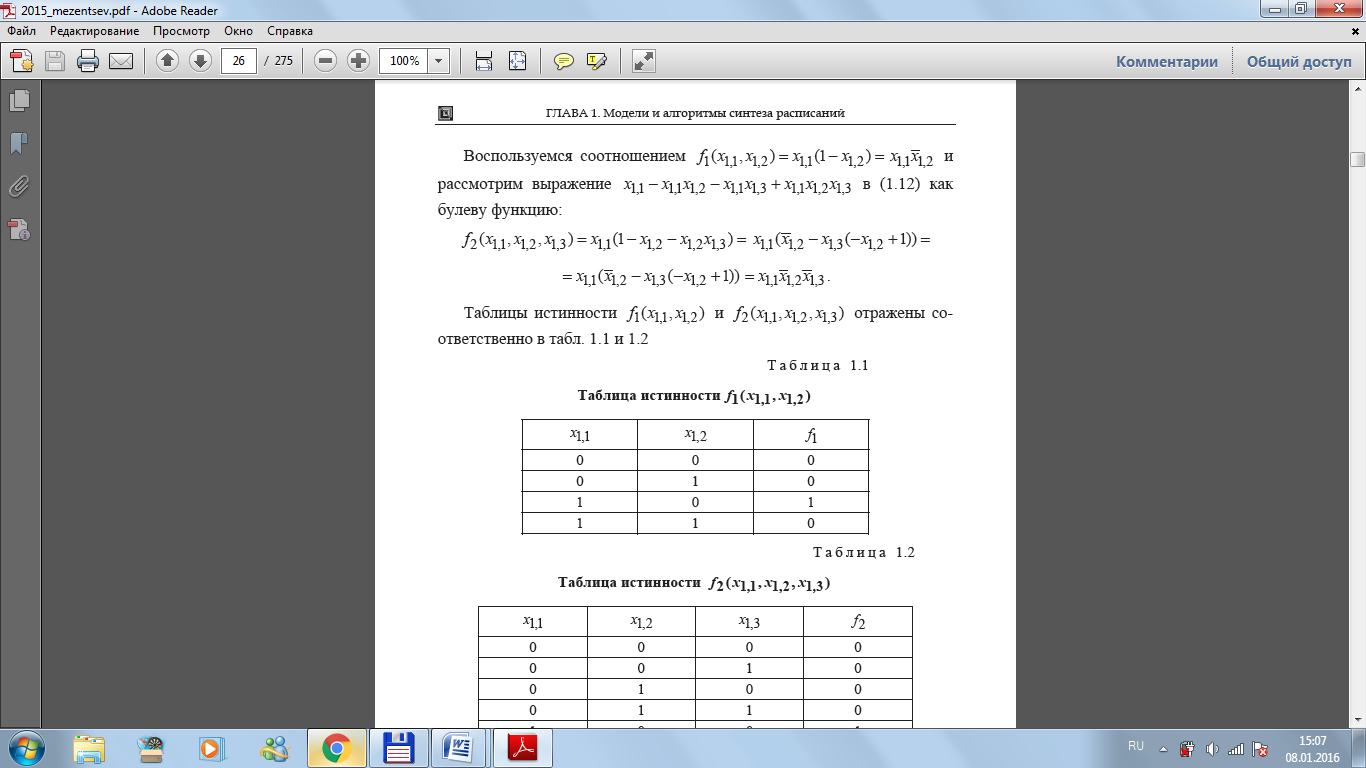
В
булевой функции
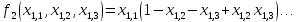
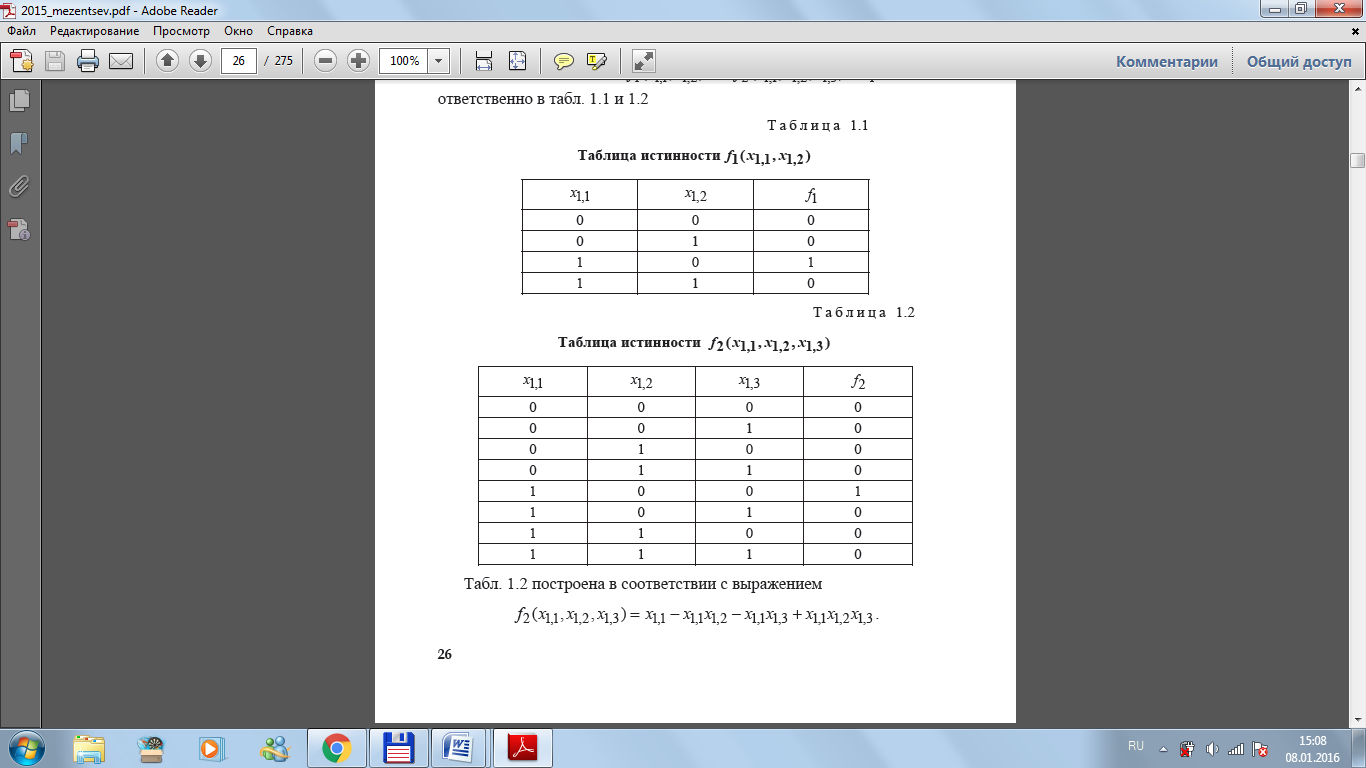

Таким образом, при раскрытии рекурсий получается задача (1.1)-(1.4), (1.13), (1.6)-(1.8), неразрешимая точными методами.
Для преобразования задачи в задачу частично-целочисленного линейного программирования с булевыми переменными (ЗЛПБП).
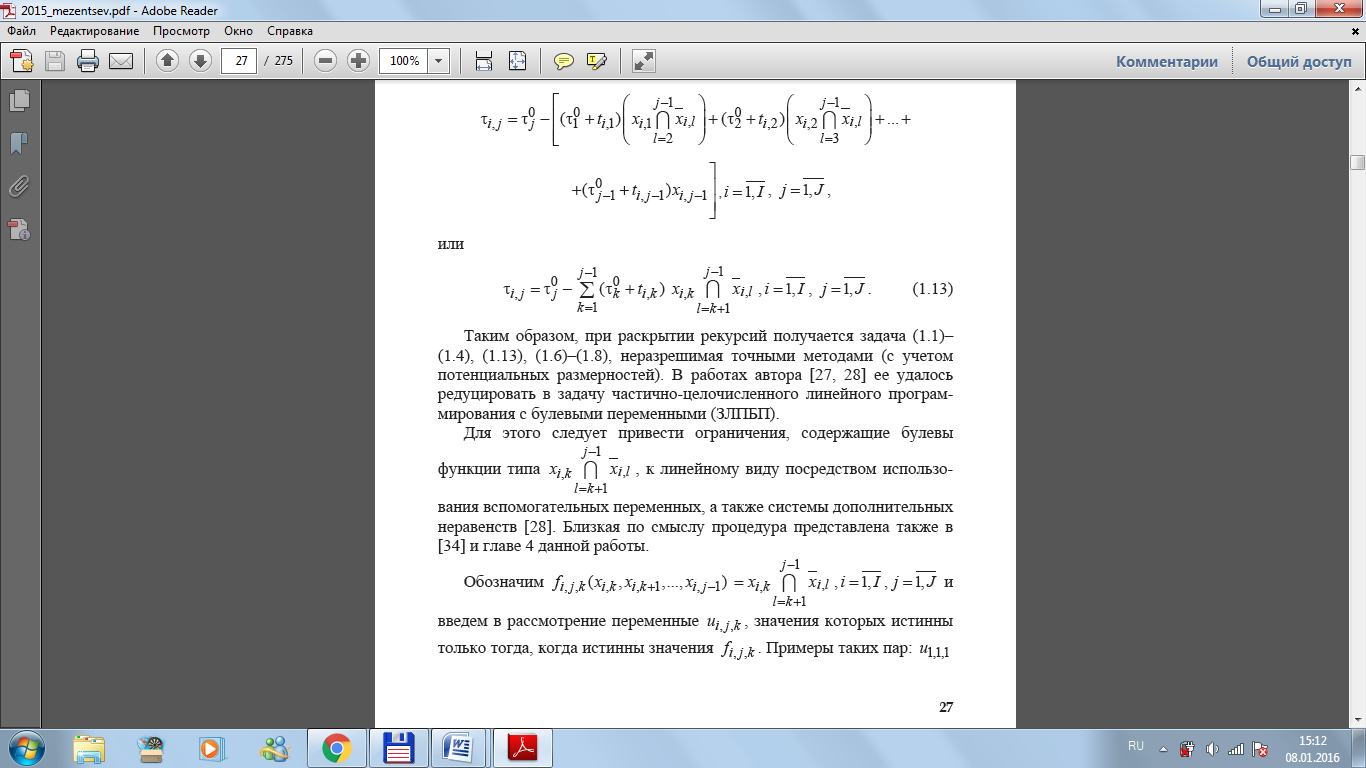
неравенств.
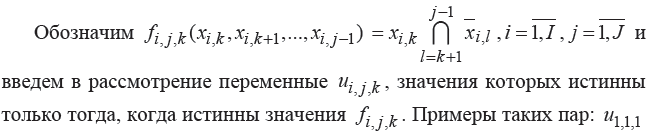

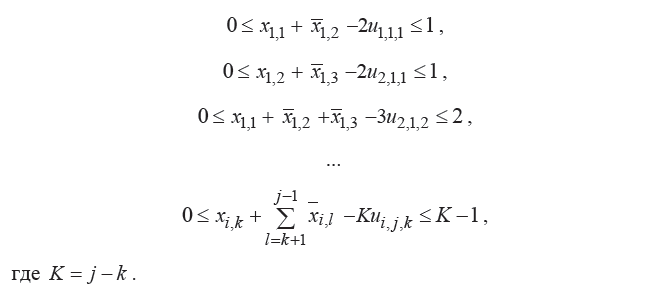
K
— максимально возможное число единиц
(число переменных x в
центральной части двойного неравенства
(в функции
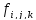 для данного случая))
для данного случая))
Соответствующие условия истинности:
0
≤
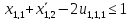
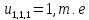 истинно при условии
истинно при условии
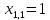 и
и
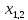 =
0 (см. табл. истинности выше ).
=
0 (см. табл. истинности выше ).
Проверим:
0
≤
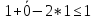
0
≤
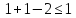 ,
верно
,
верно

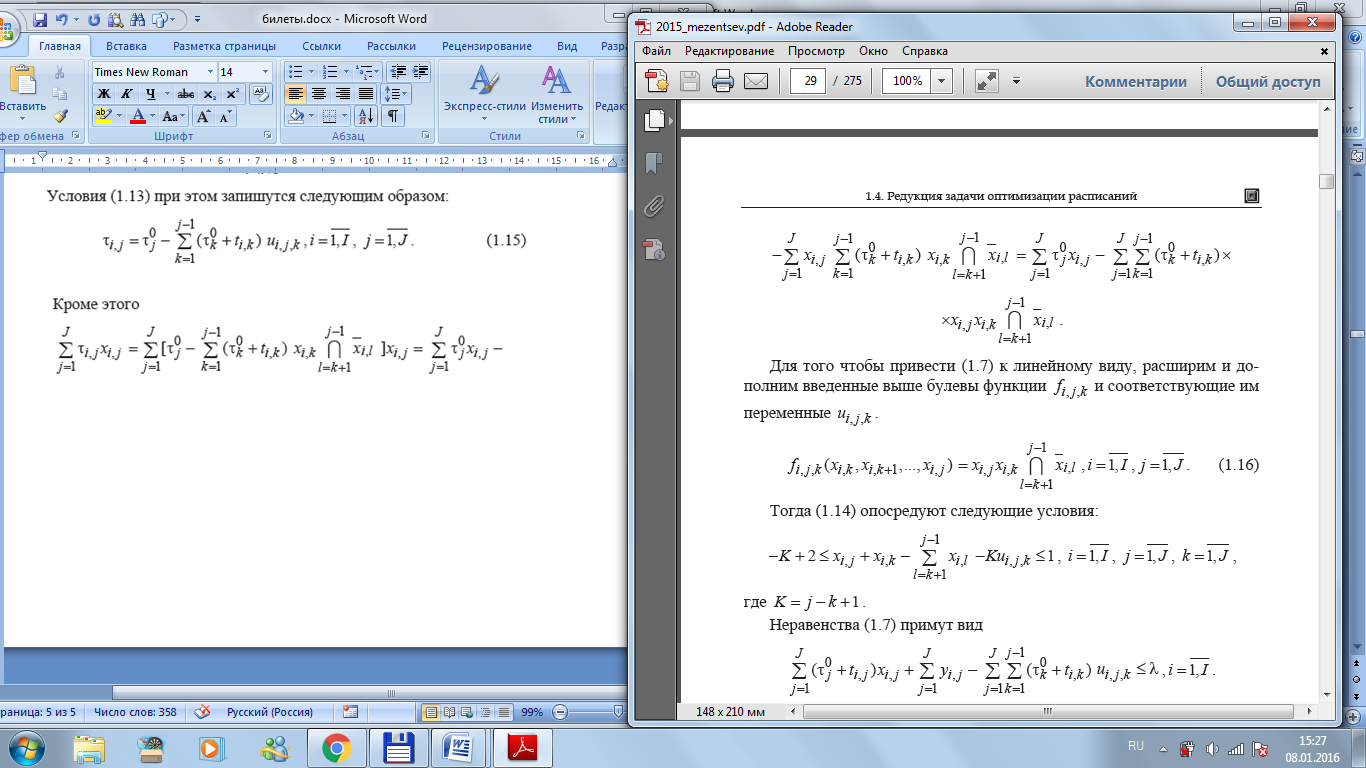
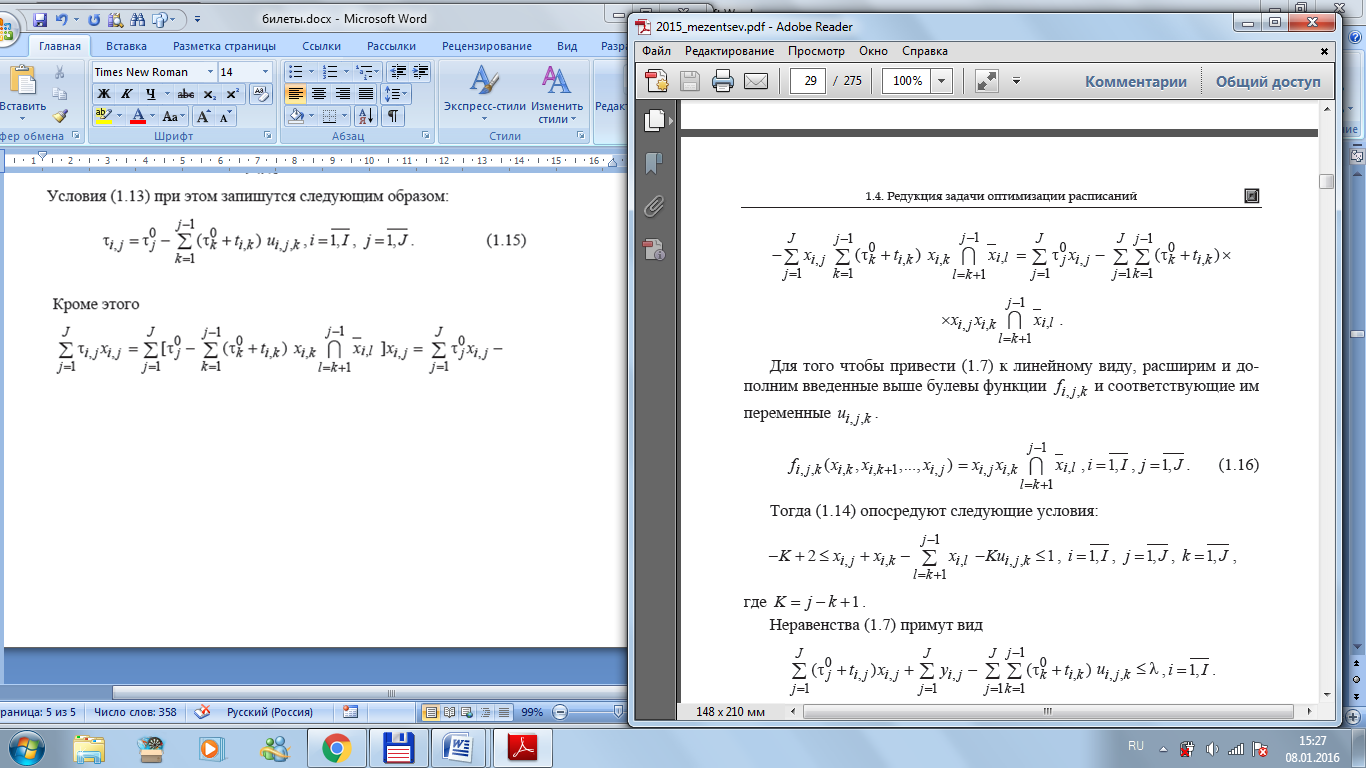
Здесь K по-прежнему
максимально возможное число единиц
(число переменных x в
центральной части двойного неравенства).
Увеличилось на 1, т.к. добавили
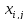
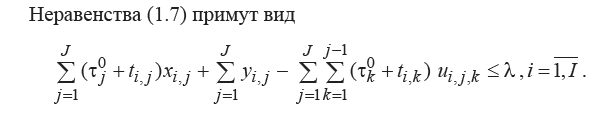
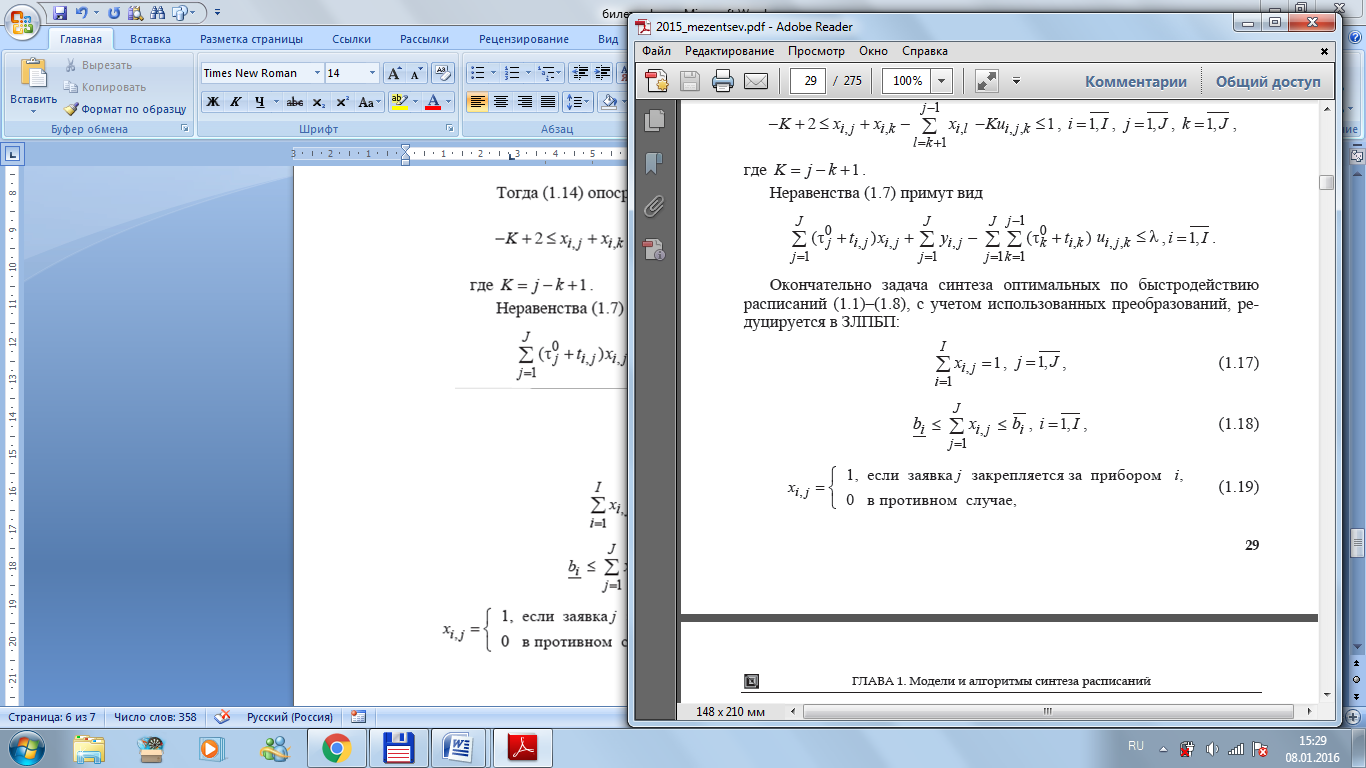
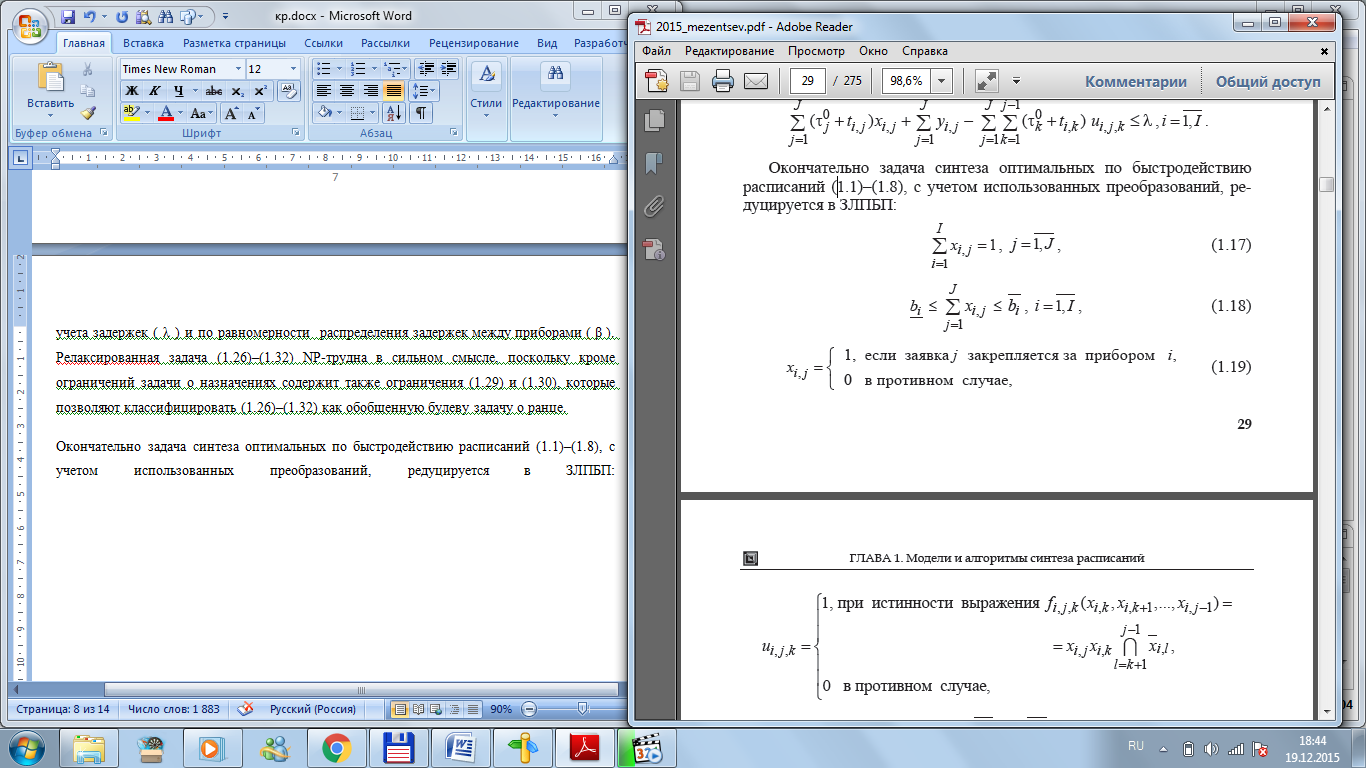
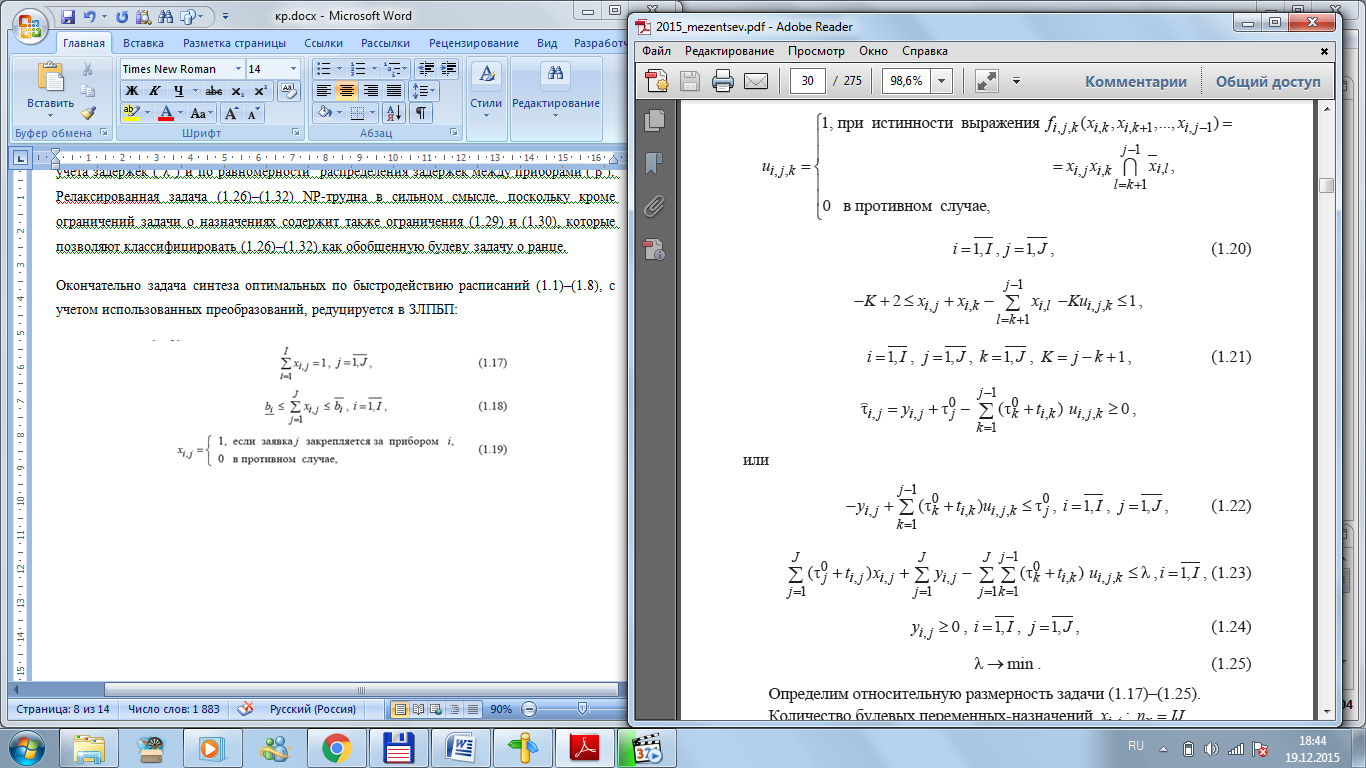
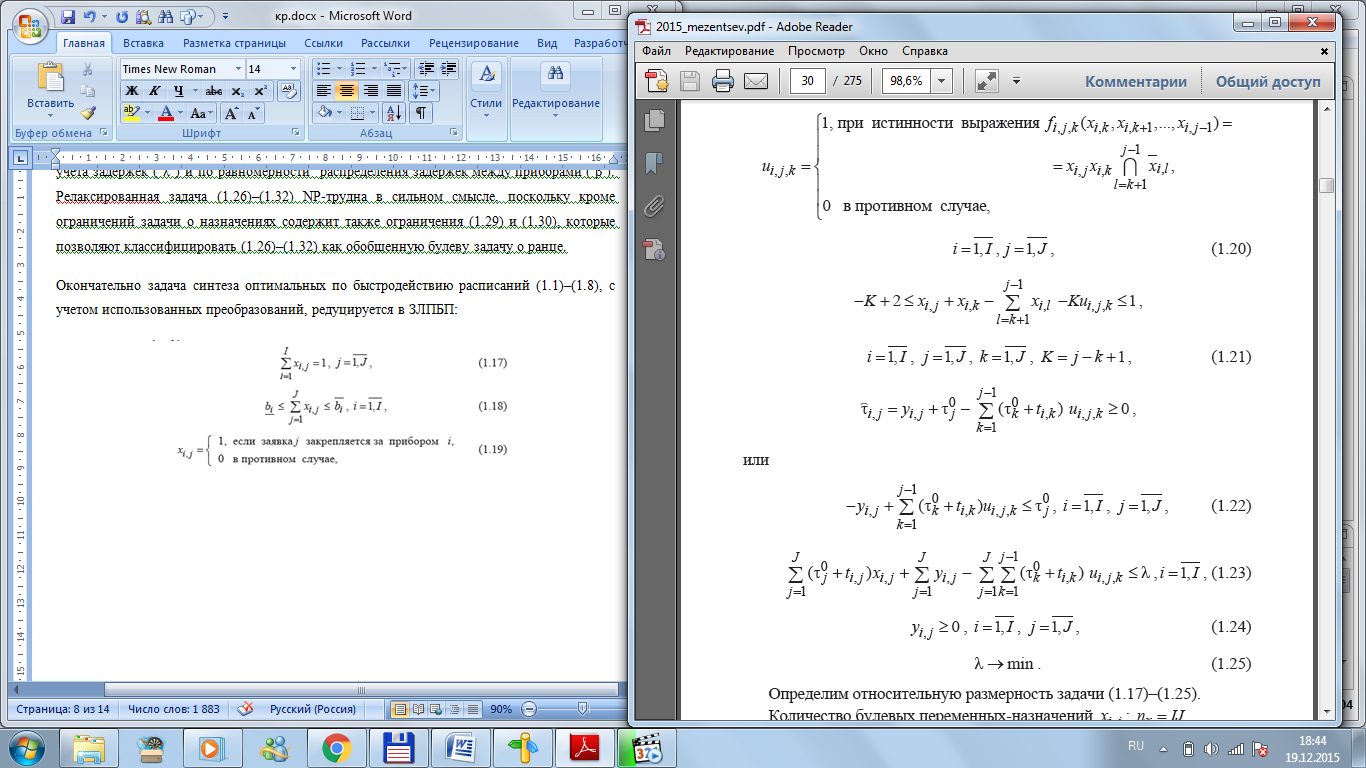
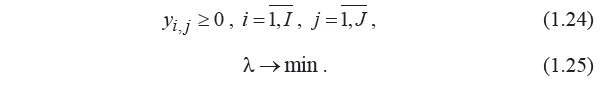
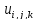 вычисляются
исходя из назначений заявок на приборы,
найденных приближенным способом (вопрос
№4).
вычисляются
исходя из назначений заявок на приборы,
найденных приближенным способом (вопрос
№4).
Пусть имеется распределение заявок по приборам:
X0
=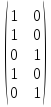
Тогда
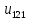 =1 ;
=1 ;
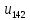 =1 ;
=1 ;
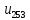 =1 Выбираются интервалы 1..0..1, где на
концах стоят 1, а в середине 0.
=1 Выбираются интервалы 1..0..1, где на
концах стоят 1, а в середине 0.
Ограничение (1.21) служит для проверки условия истинности.
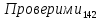 =1. К=j-k+1.
K=4-2+1=3.
=1. К=j-k+1.
K=4-2+1=3.
-K+2
≤
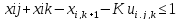 ,
,
-3+2
≤
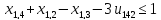
-1
≤
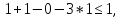 верно
верно
Ограничение (1.22) используется для вычисления компенсирующих переменных yij.
Например:
-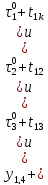 ,
,
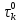 и
и
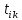 даны
в условии задачи. (k
меняется от 1 до j).
даны
в условии задачи. (k
меняется от 1 до j).
Пусть:
-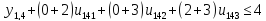 ,
,
-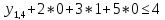 ,
,
-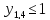 ,
,
Y ij должны быть положительны, если отрицательны, то игнорируем их.
Ограничение (1.23)
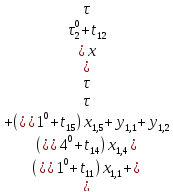 +
+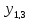 +
+ +
+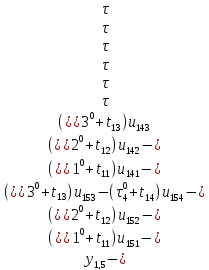
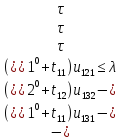
В данном примере j=5, k=j=5.
Аналогично составляется неравенство для второго прибора i=2.
Содержательное описание:
Пусть имеется ряд заявок, которые необходимо распределить между параллельными приборами при известной (различной) производительности таким образом, чтобы минимизировать суммарное время обслуживания всех заявок. Прерывания обслуживания запрещены. Пусть также известно расписание поступления заявок в параллельную обслуживающую систему (задано задержками поступления заявок, отсчитываемыми от момента времени 0). В качестве базового рассмотрим линейное обслуживание.
Редукция используется, чтобы убрать рекурсию в вычислении фактических задержек заявки. Так как переменные назначения булевы, при раскрытии используются булевы функции.
Сначала
для одного прибора расписывается
несколько подряд идущих ориентировочных
фактических задержек
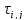 Вводятся булевы функции, используется
индукция по размерности. В результате
получаем вычисление ориентировочных
фактических задержек
Вводятся булевы функции, используется
индукция по размерности. В результате
получаем вычисление ориентировочных
фактических задержек
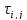 через булевы функции (в общем виде булевы
функции обозначаются fi,j,k).
Для каждой булевой функции вводится
булева переменная ui,j,k,
которая истинна только тогда, когда
истинна соответствующая булева функция.
Эти переменные вводятся вместо функций
fi,j,k
через булевы функции (в общем виде булевы
функции обозначаются fi,j,k).
Для каждой булевой функции вводится
булева переменная ui,j,k,
которая истинна только тогда, когда
истинна соответствующая булева функция.
Эти переменные вводятся вместо функций
fi,j,k
Используются следующие ограничения:
1.19 Используется булева переменная назначения заявки j на прибор i xij (1 — назначено, 0 — не назначено)
1.17 Каждая заявка назначается только на один прибор.
1.18 Количество назначений заявок на один прибор ограничено сверху и снизу (в общем случае не менее 0 и не более общего числа заявок)
1.20 Для каждой булевой функции fi,j,k, зависящей от переменных с xik по x i,j-1 вводится булева переменная ui,j,k, которая истинна только тогда, когда истинна соответствующая булева функция.
1.21 Записывается ограничение, задающее условие истинности переменной ui,j,k Смысл его сложно описать. K — максимально возможное число единиц (число переменных x в центральной части двойного неравенства).
1.22 используется для вычисления компенсирующих переменных yij. Нас интересуют только неотрицательные.
В
общем, во все ограничения вместо
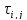 подставляется выражение для этой
переменной, использующее ui,j,k
Фактическая задержка
подставляется выражение для этой
переменной, использующее ui,j,k
Фактическая задержка
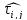 теперь явно также не вычисляется. Явный
смысл некоторых ограничений не так
очевиден из-за преобразований.
теперь явно также не вычисляется. Явный
смысл некоторых ограничений не так
очевиден из-за преобразований.
Критерий остается тем же. Суммарное время обработки заявок на приборе i ограничено сверху числом λ (и так для каждого прибора), λ минимизируется.
