
- •Содержание
- •1. Содержательная постановка задачи синтеза оптимальных расписаний параллельно-последовательной обслуживающей системы.
- •2. Постановка задачи оптимизации расписаний параллельной системы с задержками поступления заявок
- •3. Редукция задачи оптимизации расписаний параллельной системы в задачу частично-целочисленного линейного программирования
- •4. Бикритериальная упрощенная формулировка задачи синтеза расписаний параллельной системы и алгоритм решения
- •5. Декомпозиционные приближенные алгоритмы оптимизации расписаний параллельной системы с задержками поступления заявок. Жадный алгоритм и бикритериальное приближение.
- •6. Динамическое программирование с отсевом вариантов в оптимизации расписаний параллельной системы с задержками поступления заявок
- •7. Последовательные многостадийные обслуживающие системы. Моделирование на смешанных сетях.
- •8. Модификации метода ветвей и границ оптимизации расписаний последовательных многостадийных обслуживающих систем (jsp)
- •9. Алгоритм неполной декомпозиции задач оптимизации расписаний последовательных обслуживающих систем.
- •10. Многостадийные параллельно-последовательные обслуживающие системы. Подходы к формализации задач управления.
- •11. Декомпозиционный алгоритм оптимизации расписаний многостадийных параллельно-последовательных обслуживающих систем
- •12. Приложение моделей и алгоритмов оптимизации расписаний многостадийных параллельно-последовательных систем.
- •13. Содержательная постановка задачи управления материальными потоками предприятия
- •14. Формальная постановка задачи оптимизации управления входными и выходными материальными потоками
- •15. Задача оптимизации поставок сырья и комплектующих на предприятии. Содержательная постановка.
- •16. Формальная постановка задачи оптимизации поставок
- •17. Определение оптимальных цен продаж в задаче оптимизации управления входными и выходными материальными потоками
- •18. Декомпозиционный алгоритм решения задачи оптимизации поставок
- •19. Программные средства (пс) оптимизации управления входными и выходными материальными потоками предприятия (целиком из монографии)
- •20. Пс оптимизации расписаний последовательных, параллельных и параллельно-последовательных систем
- •21. Имитационное моделирование производственных систем и процессов. Языки, системы им.
- •22. Основные блоки сим Арена и их атрибуты.
- •23. Основные операторы языка gpss.
- •24. Моделирование параллельных систем в сим Арена
- •25. Моделирование последовательных систем в сим Арена.
- •26. Моделирование параллельных систем в gpss world.
- •27 Моделирование последовательных систем в gpss world.
- •28. Среда ibm ilog cplex studio. Назначение, возможности, задачи моделирования, разрешимые и неразрешимые в этой среде.
- •29. Проекты ibm ilog cplex studio, состав, назначение компонент. Основные элементы языка opl.
- •Задача №1.
- •Задача №2. Job Shop
Задача №2. Job Shop
Найти оптимальное по быстродействию расписание последовательной системы (JSP)
|
Матрица маршрутов |
|
Матрица времени обслуживания |
||||||
|
1 |
2 |
1 |
3 |
4 |
4 |
|||
|
2 |
1 |
2 |
4 |
2 |
5 |
|||
|
1 |
3 |
1 |
1 |
6 |
4 |
|||
Обозначим тройкой (i,j,q) операцию обслуживания детали i станком j в q-й по очереди раз. Построим дизъюнктивную сетевую модель обслуживающей системы в представлении «узел-операция» (рисунок 1). Дуги (стрелки) обозначают последовательность выполнения операций, ребра (прямые линии) — конфликты за станок.

Рисунок 1 — Дизъюнктивная сеть
Экономико-математическая модель задачи в общем виде представлена формулами 1–6.
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Формула 4 по-другому может быть записана в виде формул 5 и 6.
 время начала выполнения операции i
(5)
время начала выполнения операции i
(5)
 (6)
(6)
Булевы
переменные
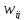 =1,
если операцию i решено выполнять
раньше операции j, и
=1,
если операцию i решено выполнять
раньше операции j, и
 =0
в противном случае.
=0
в противном случае.
B>0 — некоторое большое число, превышающее величиной длительность самой трудоемкой операции в системе. Примем его равным 100.
 —
время выполнения операции i
—
время выполнения операции i
Для рассматриваемой задачи экономико-математическая модель представлена формулами 7–28.
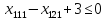 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
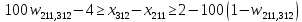 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
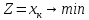 (28)
(28)
Для решения данной задачи будем использовать алгоритм ветвей и границ.
Ранжируем все ребра смешанной сети по убыванию конфликтности, которая определяется количеством конкурирующих относительно одного и того же агрегата требований в каждый интервал времени. Получаем следующее упорядоченное множество из десяти элементов:
V
= { ,
,
 ,
,


 }
}
Точно не знаю, как ранжировать ребра. Я использовала матрицу маршрутов и матрицу времени обслуживания.

Убрала
конфликты и нарисовала диаграмму Ганта
обработки партий деталей. Партии
подписаны слева, на отрезках написаны
номера станков. Если идти от 0 направо,
видны однозначные конфликты (когда
интервалы, требующие одинаковые станки,
заходят друг на друга). Это
 ,
,
 Далее конфликтность я определяла в
зависимости от расстояния между
интервалами, требующими один станок.
Опять идем от 0 направо. Между операциями
111 и 211 интервал 1 час, так же как между
операциями 211 и 112, 211 и 312. Ранжируем
Далее конфликтность я определяла в
зависимости от расстояния между
интервалами, требующими один станок.
Опять идем от 0 направо. Между операциями
111 и 211 интервал 1 час, так же как между
операциями 211 и 112, 211 и 312. Ранжируем

 .
Между операциями 311 и 211 интервал 3 часа.
Между операциями 111 и 312 интервал 4 часа.
Между операциями 311 и 112 интервал 6 часов.
.
Между операциями 311 и 211 интервал 3 часа.
Между операциями 111 и 312 интервал 4 часа.
Между операциями 311 и 112 интервал 6 часов.
Для оценки нижней границы задачи уберем все конфликты (ребра) и посчитаем критическое время как для обычного сетевого графика (рисунок 2).
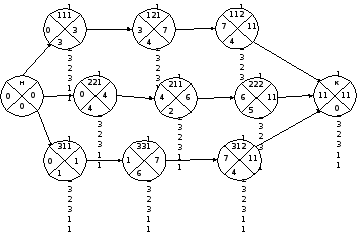
Рисунок 2
Получили, что минимально возможное время обработки трех партий деталей — 11 часов, то есть, нижняя граница решения — 11 часов.
Выбирать ребра будем по принципу максимального приоритета (для чего и ранжировали). При этом будем проверять сеть на отсутствие циклов.
Шаг 1. Выбираем ребро

Подзадача 1.1
 (111, затем 311)
(111, затем 311)

Подзадача 1.2
 (311, затем 111)
(311, затем 111)

Критическое время 12 минимальное. Оставляем подзадачу 1.2, выбираем следующее ребро.
Шаг 2. Выбираем ребро

Подзадача 1.2.1


Подзадача 1.2.2


Минимальным остается критическое время 12.
Шаг 3. Выбираем ребро

Подзадача 1.2.1.1


Подзадача 1.2.1.2


Минимальное критическое время по всем висячим вершинам — 13
Шаг 4. Выбираем ребро

Подзадача 1.2.1.1.1


Подзадача 1.2.1.1.2


Минимальное критическое время по всем висячим вершинам — 14 (подзадача 1.1). Возвращаемся к этой подзадаче.
Шаг 2. Выбираем ребро

Подзадача 1.1.1


Подзадача 1.1.2


Минимальное критическое время по всем висячим вершинам — 14 (подзадача 1.1.1).
Шаг 3. Выбираем ребро

Подзадача 1.1.1.1


Подзадача 1.1.1.2


Минимальное критическое время по всем висячим вершинам — 14 (подзадача 1.1.1.1).
Шаг 4. Выбираем ребро

Подзадача 1.1.1.1.1


Подзадача 1.1.1.1.2


Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2).
Шаг
5. Выбираем ребро
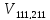
Подзадача 1.2.1.1.2.1

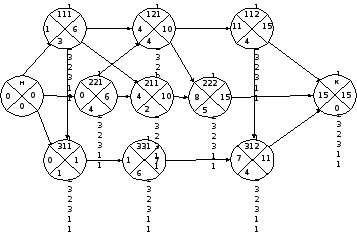
Подзадача 1.2.1.1.2.2


Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2.1).
Шаг 6. Выбираем ребро

Подзадача 1.2.1.1.2.1.1


Подзадача 1.2.1.1.2.1.2


Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2.1.1).
Шаг 7. Выбираем ребро

Подзадача 1.2.1.1.2.1.1.1


Подзадача 1.2.1.1.2.1.1.2

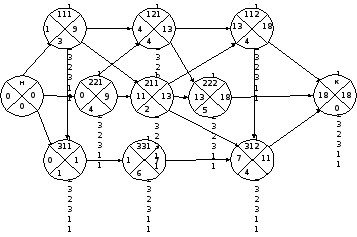
Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2.1.1.1).
Шаг 8. Выбираем ребро

Подзадача 1.2.1.1.2.1.1.1.1


Подзадача 1.2.1.1.2.1.1.1.2
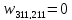
Здесь цикл 111 – 211 – 311 - 111

Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2.1.1.1.1).
Шаг 9. Выбираем ребро

Подзадача 1.2.1.1.2.1.1.1.1.1


Подзадача 1.2.1.1.2.1.1.1.1.2

Здесь цикл 111 – 211 – 312 - 111

Минимальное критическое время по всем висячим вершинам — 15 (подзадача 1.2.1.1.2.1.1.1.1.1).
Шаг 10. Выбираем ребро
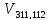
Подзадача 1.2.1.1.2.1.1.1.1.1.1


Подзадача 1.2.1.1.2.1.1.1.1.1.2

Здесь цикл 111 – 121 – 112 – 311 - 111

Минимальное критическое время — 15.
В итоге имеем следующую сеть:

Трактовка:
Из данной сети берем раннее время начала каждой операции. Получаем расписание:
|
Партия |
Длительность обработки (t), час |
Время начала обработки (x) (раннее время начала) |
Маршруты (номера станков) |
|||||||
|
Деталь 1 |
3 |
4 |
4 |
1 |
4 |
11 |
1 |
2 |
1 |
|
|
Деталь 2 |
4 |
2 |
5 |
0 |
4 |
8 |
2 |
1 |
2 |
|
|
Деталь 3 |
1 |
6 |
4 |
0 |
1 |
7 |
1 |
3 |
1 |
|
Решение CP для проверки:
// solution with objective 15
itvs = [[<1 1 4 3>
<1 4 8 4> <1 11 15 4>]
[<1 0 4 4> <1 4 6 2> <1 8 13 5>]
[<1 0 1 1> <1 1 7 6> <1 7 11 4>]];
mchs = [{} {<"itvs[2][0]" 0 3 0 0 1 1>
<"itvs[0][0]" 1 0 1 1 4 3>
<"itvs[1][1]" 2 2 2 4 6 2>
<"itvs[2][2]" 3 4 3 7 11 4>
<"itvs[0][2]" 4 1 4 11 15 4>} {
<"itvs[1][0]" 0 1 0 0 4 4>
<"itvs[0][1]" 1 0 1 4 8 4>
<"itvs[1][2]" 2 2 2 8 13 5>}];
// solution with objective 15
1 4 11
0 4 8
0 1 7
Дерево решений:

