12. Приложение моделей и алгоритмов оптимизации расписаний многостадийных параллельно-последовательных систем.

Постановка (2.7)-(2.20) из вопроса 10

Содержательный ответ:

Рассмотрим подход, использующий модели и алгоритмы вопросов 3, 4, 5. Пример — задача планирования строительства скважин с явным заданием последовательности бурения.

2.22 Введем дополнительно к переменным моделей вопросов 3 и 4 неотрицательное время начала бурения скважины (куста скважин) под номером j

2.23 Используется булева переменная назначения кусту j буровой i x_ij (1 — назначено, 0 — не назначено)

2.24 Каждый кус скважин назначается только на одну буровую.

2.25 Количество назначений кустов скважин на одну буровую ограничено сверху и снизу.

2.26 задает ограничение непосредственного предшествования-следования операций обработки двух кустов скважин: бурение последующего куста (время начала бурения скважины) начинается не раньше, чем закончится бурение предыдущего куста (определяется как сумма времени начала бурения предыдущего куста и длительности его обработки)

2.27 Для замыкающих кустов время окончания их обработки (как время начала обработки плюс длительность обработки) не позднее λ

2.28 Длительность обработки принятых заявок (назначенных кустов) для каждой буровой не должна превышать λ.

2.29 λ минимизируется (1.31).

13. Содержательная постановка задачи управления материальными потоками предприятия

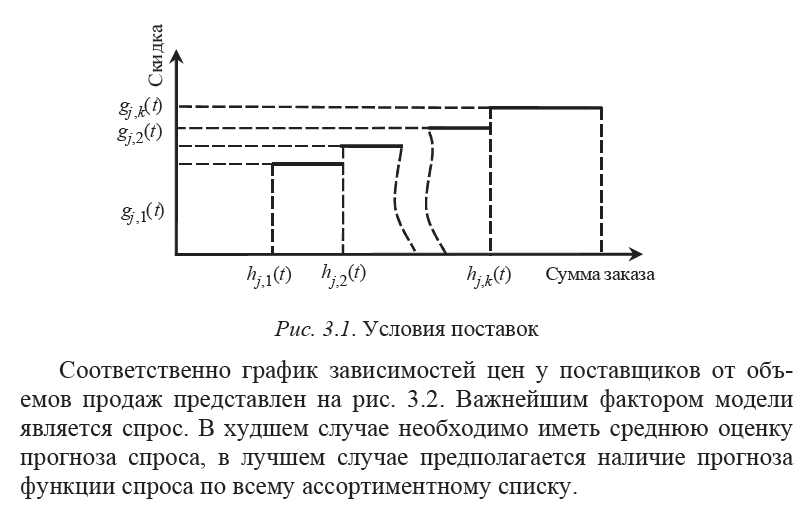
волнистая пунктирная линия обозначает разрыв изображения. То есть, функция состоит из многих ступеней (в том числе плоской, обозначающей скидку 0%), число их K

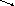
У каждого поставщика j в каждом периоде t свои условия поставок.

Исходный рисунок не совсем корректен, в матмодели по-другому. Обозначения описаны в вопросе 14.

При сумме заказа по (интервал [0; ] ) скидка (0%), на интервале (] скидка и т.д. я в реализации принимала очень большим числом, при превышении которого функция скидок не определена.

Вообще это стандартная ступенчатая функция скидок, с которой все сталкивались. Например: при покупке на сумму до 3 000 рублей скидки нет, 3 001-5 000 — скидка 3%, 5001-7000 — скидка 5%, 7 001 и больше (можно принять условно 7 000-1 000 000) — скидка 10%

На двух остальных графиках переменными обозначены тоже правые границы интервалов, сопоставление значения переменной оси y интервалу оси x по аналогии. У каждого поставщика j в каждом периоде t своя зависимость цены от суммы заказа. У каждой группы потребителей l по каждому товару i в каждом периоде t своя функция спроса.

Система скидок здесь — разделение потребителей на группы и установление для каждой группы своей цены продажи по всему ассортиментному списку. Например, оптовые и розничные покупатели. Спрос разных групп потребителей будет тоже разным.

14. Формальная постановка задачи оптимизации управления входными и выходными материальными потоками

Объем закупок в стоимостном выражении d у поставщика j в месяце t вычисляется так: умножаем базовую цену C купленного у него товара i на количество этого товара y, получаем стоимостное выражение объема закупок товара i у поставщика j в месяце t. Суммируем эти суммы по всем товарам i, получаем общую сумму закупки у поставщика j в месяце t.

Ограничение 3.2 призвано показать попадание стоимостного выражения объема закупок в один из интервалов суммы заказа, который определяет размер скидки. Соответственно, — стоимостное выражение не попало в интервал скидки с номером k, 1 — попало. Если считать, что h — правая граница интервала, данное ограничение не кажется мне верным, но переделывать его сама я не буду.

Ограничение 3.4 показывает, что деньги, которыми мы располагаем в периоде t — оборотный капитал — тратится на закупку товаров со скидками (скидка выбирается с помощью переменной-индикатора попадания в интервал) и идет в остаток. То есть, у поставщика j перебираем интервалы сумм заказов от 1 до K, определяем по стоимостному выражению объема закупок у него скидку, отнимаем от стоимостного выражения объема закупок сумму скидки, получаем итоговую сумму, которую потратили на закупку товаров у поставщика j. Так для каждого поставщика, суммируем все, что потратили на закупку товара. Плюс останется оборотный капитал, сумма общих затрат на закупку и остатка равна сумме денег (оборотному капиталу), которой мы располагали.

Определение размера скидки (алгоритм расписывала в вопросе 13). Последнее неравенство мне кажется неправильным (после интервала K функция обрывается, там нет скидки). Я бы его заменила на

так как обозначает правую границу последнего интервала.

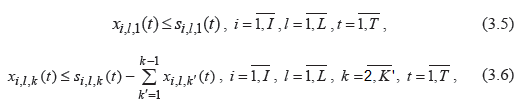
Смысл ограничений 3.5 и 3.6: на первом интервале функции спроса группы потребителей l на товар i в периоде t объем продаж не больше, чем спрос на этом интервале. Для остальных интервалов k объем продаж не превышает оставшийся размер спроса: разность между спросом на выбранном интервале k и суммой объемов продаж на интервалах до выбранного (с 1 до k-1).

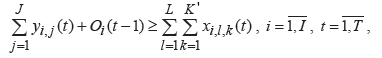
Смысл ограничения 3.7: объем продаж каждого товара i в натуральном выражении в периоде t (по всем интервалам функции спроса у всех групп потребителей) не меньше, чем суммарный объем закупок этого товара у всех поставщиков в периоде t и остаток этого товара с предыдущего периода.

Смысл ограничения 3.8: остаток товара i в периоде t равен разности объема этого товара, который имелся в периоде t (суммарный объем закупок у всех поставщиков в периоде t и остаток с предыдущего периода), и суммарного объема продаж этого товара в периоде t на всех интервалах функций спроса всех групп потребителей.

Смысл ограничения 3.9. остаток оборотного капитала в периоде t равен разности между тем, что имелось (остаток оборотного капитала с предыдущего периода t-1 и выручка предыдущего периода как сумма произведений цены продажи товара i на интервале функции спроса k группы потребителей l на объем продажи этого товара на интервале функции спроса k группы потребителей l), и тем, что ушло (накладные расходы предыдущего периода и стоимостное выражение суммарного объема закупок текущего периода с учетом скидки)

ЭФФЕКТИВНЫЙ АЛГОРИТМ ПРИБЛИЖЕННОГО РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ УПРАВЛЕНИЯ ВХОДНЫМИ И ВЫХОДНЫМИ МАТЕРИАЛЬНЫМИ ПОТОКАМИ

То есть, вместо функции скидок для каждого поставщика выбираем какое-то одно значение скидки (для каждого рассматриваемого периода). Второе ограничение здесь показывает, что в каждом периоде мы тратим всего на покупку товаров с учетом скидки (здесь уже конкретного ее значения для каждого поставщика) не больше, чем имеем оборотного капитала.

3.21 показывает, что деньги, которыми мы располагаем в периоде t — оборотный капитал — тратится на закупку товаров со скидками и идет в остаток. Сумма закупок (первое слагаемое): для каждого поставщика j выбирается конкретное значение скидки и вычитается из целого, затем так же, как раньше, находится стоимость покупок у этого поставщика (для всех товаров от поставщика цену умножаем на количество, затем учитываем скидку), суммируется по поставщикам.

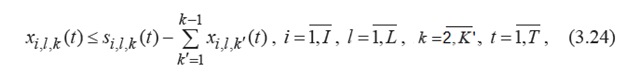
То есть, для начала выбираем для каждого поставщика максимально возможное у него значение скидки . Эти значения составят матрицу.

Замечания к выбору такие же, как для выбора скидки в формальной постановке задачи.

ИЛЛЮСТРАТИВНЫЙ ПРИМЕР. РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ ЗАКУПОК И СБЫТА ПРОДУКЦИИ
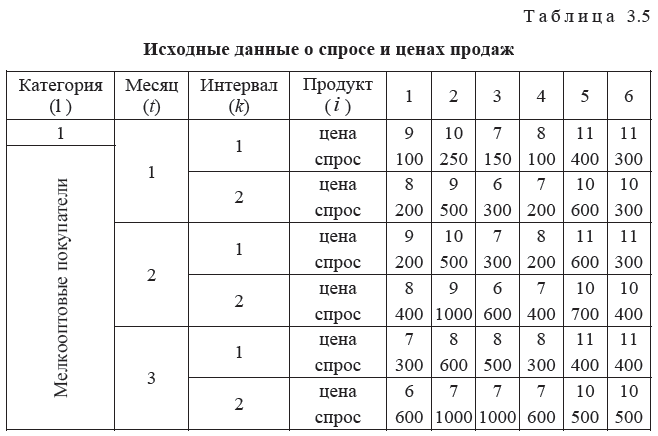