
- •Глава 1. Группировка статистических данных
- •1.1. Теория группировок
- •1.2. Решение типовых задач
- •1.3. Задачи для самостоятельной работы
- •1.4. Контрольные вопросы по теме: группировка статистических данных
- •Глава 2. Абсолютные и относительные величины
- •2.1. Абсолютные величины
- •2.2. Относительные величины
- •2.3. Решение типовых задач
- •2.4. Задачи для самостоятельной работы
- •Глава 3: Средние величины
- •3.1. Основные понятия теории средних величин
- •3.2. Решение типовых задач
- •3.3. Задачи для самостоятельной работы
- •3.4. Контрольные вопросы по теме «Средние величины»
- •Глава 4. Показатели вариации признака
- •4.1. Понятие вариации
- •4.2. Сложение дисперсий изучаемого признака
- •4.3. Вариации альтернативного признака
- •4.4. Решение типовых задач
- •4.5. Задачи для самостоятельной работы
- •4.6. Контрольные вопросы по теме «Показатели вариации признака»:
- •Глава 5. Выборочное наблюдение
- •5.1. Понятие о выборочном наблюдении
- •5.2. Принятые условные обозначения
- •5.3. Простая случайная выборка
- •5.4. Решение типовых задач
- •5.5. Задачи для самостоятельной работы
- •5.6. Контрольные вопросы по теме «Выборочное наблюдение»:
- •Глава 6. Ряды динамики
- •6.1. Понятие и виды динамических рядов
- •6.2. Показатели ряда динамики
- •6.3. Средние показатели динамики
- •6.4. Статистическое изучение сезонных колебаний
- •6.5. Решение типовых задач
- •6.6. Задачи для самостоятельной работы
- •6.7. Контрольные вопросы по теме «Ряды динамики»:
- •Глава 7. Статистические индексы
- •7.2. Индексы количественных показателей
- •7.3. Индексы качественных показателей
- •7.4. Цепные и базисные индексы
- •7.5. Изучение динамики качественных показателей по нескольким единицам (предприятиям, территориям, странам)
- •7.6. Решение типовых задач
- •7.7. Задачи для самостоятельной работы
- •7.8. Контрольные вопросы по теме «Индексы»:
- •Список рекомендуемой литературы:
7.2. Индексы количественных показателей
Индивидуальный индекс физического объема выпуска продукция характеризует изменение выпуска (реализации или потребления) одного вида продукции и определяется по формуле:
![]()
где
![]() - количество продукции данного вида в
натуральном выражении соответственно
в текущем и базисном периодах.
- количество продукции данного вида в
натуральном выражении соответственно
в текущем и базисном периодах.
Индивидуальный индекс затрат на выпуск продукции показывает изменение затрат на производство одного вида продукции и имеет следующий вид:
![]() ,
,
где
![]() и
и![]() - себестоимость единицы продукции
данного вида соответственно в текущем
и базисном периодах;
- себестоимость единицы продукции
данного вида соответственно в текущем
и базисном периодах;
![]() и
и
![]() - сумма затрат на выпуск продукции
данного вида соответственно в текущем
и базисном периодах.
- сумма затрат на выпуск продукции
данного вида соответственно в текущем
и базисном периодах.
Индивидуальный индекс стоимости продукции:
![]() ,
,
где
![]() и
и![]() -
цена единицы продукции данного вида
соответственно в текущем и базисном
периодах;
-
цена единицы продукции данного вида
соответственно в текущем и базисном
периодах;
![]() -
стоимость продукции данного вида
соответственно в текущем и базисном
периодах.
-
стоимость продукции данного вида
соответственно в текущем и базисном
периодах.
Агрегатный индекс
физического объема продукции
![]() характеризует
изменение выпуска всей совокупности
продукции и исчисляется по формуле:
характеризует
изменение выпуска всей совокупности
продукции и исчисляется по формуле:
![]() ,
,
где
![]() и
и![]() -
количество выработанных единиц отдельных
видов продукции соответственно в
отчетном и базисном периодах;
-
количество выработанных единиц отдельных
видов продукции соответственно в
отчетном и базисном периодах;
![]() - цена единицы
отдельного вида продукции в базисном
периоде.
- цена единицы
отдельного вида продукции в базисном
периоде.
Такой вариант построения агрегатного индекса был предложен Э. Ласпейресом в 1864г.
В агрегатном индексе физического объема продукции индексируемой величиной является количество продукции (q); цена (р) служит коэффициентом соизмерения (соизмерителем).
![]() ,
,
где
![]() абсолютное изменение общей стоимости
продукции за счет изменения выпуска
продукции.
абсолютное изменение общей стоимости
продукции за счет изменения выпуска
продукции.
При вычислении
индекса физического объема продукции
возможны разные решения - в зависимости
от выбора коэффициента соизмерения. В
качестве коэффициента соизмерения
можно также использовать цены отчетного
периода (![]() )
или сопоставимые (фиксированные -
)
или сопоставимые (фиксированные -![]() ).
Тогда формулы агрегатного индекса имеют
следующий вид:
).
Тогда формулы агрегатного индекса имеют
следующий вид:
![]()
Агрегатный индекс с соизмерителями отчетного периода был предложен в 1874 г. Г. Пааше.
Кроме того, в качестве соизмерителей могут быть использованы себестоимость единицы продукции, а также затраты рабочего времени на единицу продукции. В этом случае агрегатный индекс физического объема определяется по формулам:
![]() ;
;
![]()
где
![]() -
себестоимость единицы продукции каждого
вида в базисном периоде;
-
себестоимость единицы продукции каждого
вида в базисном периоде;
![]() -
затраты рабочего времени на производство
единицы продукции каждого вида в базисном
периоде.
-
затраты рабочего времени на производство
единицы продукции каждого вида в базисном
периоде.
Средние взвешенные индексы физического объема продукции применяются в том случае, если известны индивидуальные индексы объема по отдельным видам продукции и стоимость отдельных видов продукции (или затраты на отдельные виды продукции) в базисном или отчетном периоде.
Средний взвешенный арифметический индекс физического объема продукции:
![]() ,
,
![]() - индивидуальный
индекс по каждому виду продукции;
- индивидуальный
индекс по каждому виду продукции;
![]() - стоимость продукции
каждого вида в базисном периоде.
- стоимость продукции
каждого вида в базисном периоде.
Средний взвешенный гармонический индекс физического объема продукции:
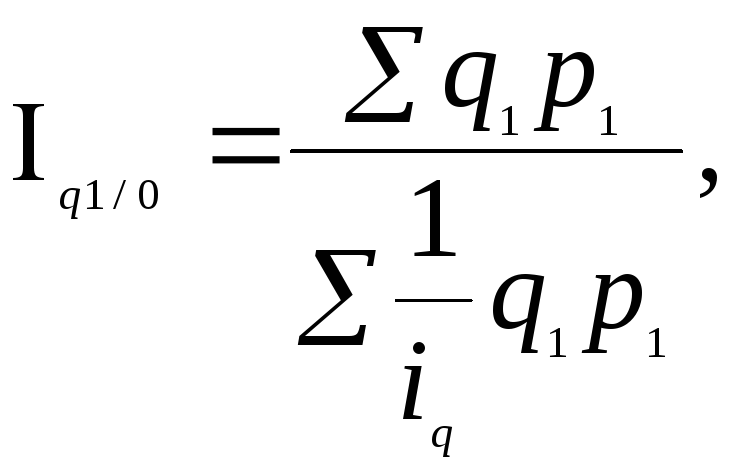
где
![]() - стоимость продукции каждого вида в
текущем периоде.
- стоимость продукции каждого вида в
текущем периоде.
Агрегатный индекс затрат на выпуск всей продукции имеет следующий вид:

где
![]() и
и![]() - затраты на выпуск продукции каждого
вида, соответственно в отчетном и
базисном периодах.
- затраты на выпуск продукции каждого
вида, соответственно в отчетном и
базисном периодах.

![]() -
абсолютное изменение обшей суммы затрет
на выпуск продукции за счет изменения
количества выработанной продукции и
ее себестоимости.
-
абсолютное изменение обшей суммы затрет
на выпуск продукции за счет изменения
количества выработанной продукции и
ее себестоимости.
Агрегатный индекс стоимости продукции (товарооборота):
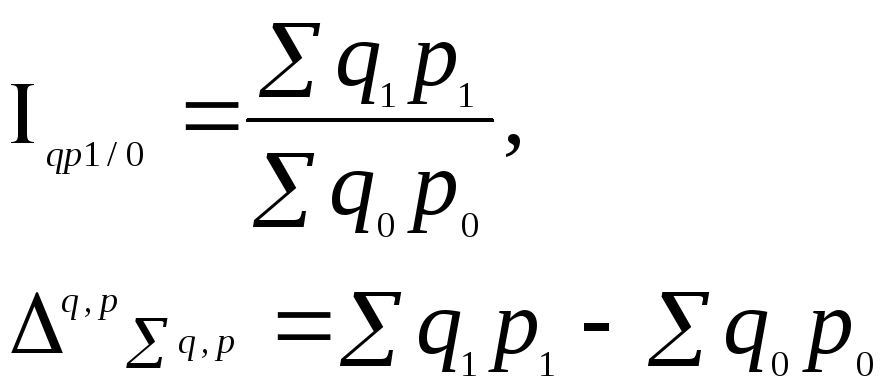
![]() -
абсолютное изменение общей стоимости
продукции за счет изменения количества
продукции и цен.
-
абсолютное изменение общей стоимости
продукции за счет изменения количества
продукции и цен.
Агрегатный территориальный индекс физического объема производства (реализации) продукции имеет вид:
![]()
![]() ,
,
где
![]() - количество выпущенной (реализованной)
продукции каждого вида в натуральном
выражении соответственно на территорииВ
и Г;
- количество выпущенной (реализованной)
продукции каждого вида в натуральном
выражении соответственно на территорииВ
и Г;
![]() - средняя цена
каждого вида продукции по сравниваемым
территориям, определяемая как средняя
взвешенная арифметическая.
- средняя цена
каждого вида продукции по сравниваемым
территориям, определяемая как средняя
взвешенная арифметическая.
