1.2. Переопределенные системы уравнений. Метод наименьших квадратов

Переопределенные системы уравнений (1.1) с матрицейA полного ранга часто встречаются на практике, например, при решении геодезиче­ских задач на водных путях, нахождении координат расположения судов в открытых акваториях по данным измерений, в процессе обработки резуль­татов измерений деталей машин и механизмов, при управлении качеством продукции в серийном производстве и др. C переопределенными система­ми уравнений приходится иметь дело в информационно-измерительных и управляющихкомплексах различного назначения, аппаратных средствах автоматизации технологических процессов и т.п.[6].

Поскольку измерения выполняются с погрешностями и математиче­ская модель, как правило, не в полной мере адекватна объекту, переопре­деленная система позволяет "сгладить" влияние погрешностей на конеч­ный результат. B этом случае принято говорить об оценивании параметров модели по экспериментальным данным, согласно выбранным критериям [13].B простых ситуациях такими критериями могут быть различные нормы мат­риц и векторов: спектральная норма, l - норма,  - норма, эвклидова (сфери­ческая) норма и др.

Среди наиболее широко распространенных методов оценивания сле­дует отметить метод наименьших квадратов [44], [52]. Его популярность объясняет­ся, очевидно, тем, что он может быть применен в любом случае — как при наличии распределения вероятностей наблюдений, так и при их отсутст­вии. Если уровень помех пренебрежимо мал в сравнении с полезными сиг­налами, а экспериментальные данные модели, структура которой известна точно, являются информационными, то для линейных уравнений коэффи­циенты модели оцениваются точно.

B других случаях оценки, полученные при отсутствии распределе­ний методом наименьших квадратов, могут иметь плохие характеристики, но в таких ситуациях ничего лучшего сделать невозможно. При опреде­ленном распределении вероятностей (например, нормальном) оценки на основе этого метода могут даже обладать оптимальными статистическими свойствами.

Метод наименьших квадратов используется в задачах "подгонки" статических характеристик.

Рассмотрим линейную стационарную модель системы, содержащую аддитивные составляющие

s = a₁y₁ + a₂ y₂ + ...+ a_n y_n+ v, (1.9)

где a₁,...,a_n –постоянные коэффициенты,

y₁,...,у_n — входные сигналы,

s- выходной сигнал,

v— сигнал помехи (шум измерений).

Предположим, что в процессе работы системы одновременно в фик­сированные моменты времени измеряются входные сигналы и сигнал s. Обозначим их значения в моменты t₁, t₂, ..., t_m, соответственно, ин­дексами 1, 2, ..., т. Поскольку все измерения, в соответствии с вы­бранной моделью, отвечают (1.9), можно составить систему уравнений

s₁ = а₁y₁₁ + а₂у₁₂ + ...+ a_ny_1n + v₁, (1.10)

s₂ = а₁y₂₁ + а₂у₂₂ + ...+ a_ny_2n + v₂,

…………………………………

s_m = а₁y_m1 + а₂у_m2 + ...+ a_ny_mn + v_m.

Введемвекторы

s = [s₁s₂ ... s_m]^T, х = [a, а₂ ... a_n]^T, v = [v₁ v₂ … v_m]^T.

Из входных данных образуем прямоугольную матрицу H размерно­сти

(т xn)

Тогда (1.10) можно записать в векторно-матричной форме:

(1.11)

Если т >n, то система (1.11), представляющая собой модель изме­рителя, является переопределенной. Тогда можно найти такие значения элементов вектора x = , при которых разность

(1.12)

точнее — скалярное произведение будет принимать минималь­ное значение. Задачу минимизации скалярного произведения сформулиру­ем следующим образом: определим вектор , при котором минимизи­руется критерий качества

(1.13)

Постоянное число 1/2, содержащееся в(1.13) на вектор x* не влия­ет. Оно введено для удобства вычислений.

Если H в критерии качества (1.13) имеет минимальный ранг, равный n, то минимум J(х) можно найти путем дифференцирования Jпox и при­равнивания производной к нулю. Это необходимое условие оптимально­сти. Достаточным условием минимума функции одной переменной следу­ет считать положительное значение второй производной в экстремальной точке, а для функции нескольких переменных должно выполняться усло­вие Лежандра-Клебша.

Рассмотрим произведение двух вектор-функций:

где 'Т" – знак транспонирования.

Согласно правилам векторного дифференцирования, можно записать

Используя это выражение, приравняем и Тогда необходимое условие оптимальности можно пред­ставить следующим образом:

(1.14)

или

Информационная матрица имеет размерность (nxn) и явля­ется неособенной, поскольку Hимеет максимальный ранг. Тогда, умножая левую и правую части (1.14) слева на инверсную матрицу , по­лучим наилучшую оценку вектора x

(1.15)

Получив наилучшую оценку вектора , подставим это значение в уравнение (1.11) и определим вектор у_м как результат моделирования

(1.16)

Качество моделирования можно оценить по вектору разности между исходными данными sи моделью s_м

z= s – s_м

Уравнение (1.15) гарантирует получение минимума суммы квадра­тов элементов вектораz, т.е.

(1.17)

Для оценки эффективности моделирования можно воспользоваться эвклидовой нормой. B среде MatLABсуществует функция "norm(z,'fro')",предназначенная для ее определения. Напомним, что эвклидова норма вектора zпредставляет собой равенство evc = = 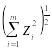. Следовательно, критерий качества (1.17) можно записать

Другой подход к получению (1.15) может состоять в следующем. Рассмотрим вновь переопределенную систему, представленную уравнением (1.11). Предположим, что v имеет нормальное распределение, а вектор s состоит из постоянных значений. Тогда Hdx = dvи, следова­тельно, dv^T= dx^T = Н^T.

Для переопределенной системы уравнений справедливо условие т >n . Умножим dv^Tсправа на вектор v и подставим его значение из уравнения (1.11)

(1.18)

Если теперь ввести критерий оценки вектора x, при котором требу­ется минимизировать

при отсутствии ограничений, то можно получить

(1.19)

Запишем (1.19) в векторно-матричной форме

(1.20)

Поскольку (1.20) совпадает с (1.18), то равенство указанного ска­лярного произведения векторов нулю возможно только в том случае, если . Данное условие может быть выполнено, если оценка х, которую ранее мы обозначили как ,будет

Мы получили уравнение, точно совпадающее с (1.16). Сумма квад­ратов погрешностей — скалярное произведение

Теперь умножим левую и правую части (1.11) слева на матрицу размерности (nЧm).Заметим, что и поэтому

где - вектор погрешности, представляющий разность между оценочным

истинным значениями вектора параметров.

Предполагая, что H и v независимы, мы получим среднее значение, равное нулю

(1.21)

Уравнение (1.21) подтверждает несмещенность оценки.

Уравнение (1.15) может быть использовано для оценки коэффици­ентов нелинейных функций, которые путем замены переменных приводят­ся к выражениям, линейным относительно неизвестных параметров.

Заметим, что использование функций для оценки параметров исходных зависимостей позволя­ет получить минимум суммы квадратов для преобразованных функций. Для исходных уравнений, являющихся нелинейными, применение нели­нейных методов оценивания позволяет получить меньшее (в сравнении с MНK) значение эвклидовой нормы. Оценка же параметров функции Z по­зволяет лишь приблизиться к наилучшей оценке y.