4. Потенциальная энергия взаимодействия электрических зарядов. Разность потенциалов

4.1. Основные формулы и соотношения

Потенциальная энергия взаимодействия двух точечных зарядов, находящихся на расстоянии r, при условии, что ,

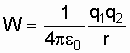.                                                               (4.1)

Потенциал электрического поля

                                                                   (4.2)

где – потенциальная энергия пробного заряда q, помещенного в данную точку поля.

Работа, совершенная силами поля по перемещению заряда q из точки 1 в точку 2, определяется по формуле

                                                         (4.3)

или

                                                            (4.4)

где – проекция вектора напряженности Е на направление . При этом интегрирование производится вдоль любой линии, соединяющей точки 1 и 2.

Разность потенциалов и напряженность электрического поля связаны соотношениями:

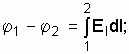                                                                (4.5)

                                                                  (4.6)

где производная берется в направлении быстрейшего изменения потенциала, то есть вдоль силовой линии.

Для однородного поля

                                                             (4.7)

где – расстояние между двумя точками, измеренное вдоль силовой линии.

Потенциал поля точечного заряда q на расстоянии r от него определяется из выражения

                                                                     (4.8)

Потенциал поля сферической поверхности радиуса , по которой равномерно распределен заряд ,

                                                                                  (4.9)

для точек, лежащих вне сферы на расстоянии от ее центра, и

                                                                (4.10)

для точек, лежащих на поверхности сферы или внутри нее.

Потенциал электрического поля, созданного точечными зарядами, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраической сумме потенциалов создаваемых отдельными точечными зарядами

                                                               (4.11)

Энергия взаимодействия системы точечных зарядов определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой:

                                                            (4.12)

где – потенциал поля, создаваемого всеми 1 зарядами (за исключением i-го) в точке, где расположен заряд .

Потенциал связан с напряженностью электрического поля соотношением:

                                                              (4.13)

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой:

                                                                (4.14)

4.2. Примеры решения задач

Задача 1. Найти разность потенциалов поля, созданного зарядами, равномерно распределенными вдоль бесконечной прямой с линейной плотностью .

Решение. Распределение потенциала во всех плоскостях, перпендикулярных к заряженной линии, одинаково. Эквипотенциальные поверхности – коаксиальные цилиндры, ось которых – заряженная линия.

Напряженность поля бесконечно длинной равномерно заряженной нити в точке, расположенной на расстоянии а от нее, , а так как разность потенциалов и напряженность электрического поля связаны соотношением отсюда

Но в бесконечности потенциал не имеет конечного значения, так как работа сил поля по удалению единичного положительного заряда из данной точки в бесконечность не имеет конечного значения. Конечное значение имеет только разность потенциалов между двумя точками поля.

Результат этот обусловлен тем, что мы считаем проводник бесконечно длинным, и, значит, нельзя говорить о точках, бесконечно удаленных от проводника, так как “бесконечно удаленная точка” физически означает точку, удаленную на расстояние, большее по сравнению с размерами проводника.

При рассмотрении реальных полей таких затруднений не возникает, так как размеры проводников конечны. Всякий заряженный проводник на достаточно большом расстоянии от него можно рассматривать как точку. Следовательно, пользуясь условным представлением реальных проводников в виде бесконечных, можно рассчитывать поле только вблизи конечного проводника (на расстояниях, малых по сравнению с длиной проводника).

Задача 2. Электрическое поле создано диполем, то есть двумя одинаковыми по величине разноименными зарядами и , находящимися на расстоянии друг от друга. Найти потенциал этого поля на расстоянии , большем по сравнению с размером диполя .

Решение. Рассматривая созданное электрическое поле как суперпозицию полей точечных зарядов и - q, выражение для потенциала в точке А, отстоящей от зарядов и на расстояниях и , можно записать в виде:

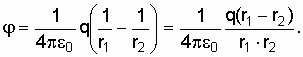
Диполь принято характеризовать вектором дипольного момента , величина которого равна произведению , а направление выбирается вдоль оси диполя от отрицательного заряда к положительному. Из рис. 4.1 следует, что при разность , а . Тогда .

Из последнего выражения следует, что потенциал поля диполя в отличие от потенциала точечного заряда, убывающего как , убывает с расстоянием как , а также зависит от направления на точку наблюдения, характеризуемого углом .

Рис. 4.1

Задача 3. Определить потенциал в центре кольца с внешним диаметром м и внутренним диаметром м, если по нему равномерно распределен заряд Кл.

Решение. Разобьем кольцо на концентрические бесконечно тонкие кольца, площадь которых , где – радиус кольца. Так как – потенциал, который создает в центре бесконечно тонкое кольцо радиусом , то

.

Умножим и разделим полученное выражение на . Отсюда

В.